Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-28T21:16:41.342Z Has data issue: false hasContentIssue false
  • English
  • Français

Receptivity coefficients at excitation of cross-flow waves by free-stream vortices in the presence of surface roughness

Published online by Cambridge University Press:  25 January 2013

V. I. Borodulin ,
A. V. Ivanov ,
Y. S. Kachanov  and
A. P. Roschektaev
V. I. Borodulin
Affiliation:
Khristianovich Institute of Theoretical and Applied Mechanics SB RAS, Institutskaya str. 4/1, Novosibirsk, 630090, Russia
A. V. Ivanov
Affiliation:
Khristianovich Institute of Theoretical and Applied Mechanics SB RAS, Institutskaya str. 4/1, Novosibirsk, 630090, Russia
Y. S. Kachanov*
Affiliation:
Khristianovich Institute of Theoretical and Applied Mechanics SB RAS, Institutskaya str. 4/1, Novosibirsk, 630090, Russia
A. P. Roschektaev
Affiliation:
Khristianovich Institute of Theoretical and Applied Mechanics SB RAS, Institutskaya str. 4/1, Novosibirsk, 630090, Russia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The present experimental study is devoted to examination of the vortex receptivity mechanism associated with excitation of unsteady cross-flow (CF) waves due to scattering of unsteady free-stream vortices on localized steady surface non-uniformities (roughness). 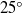The measurements are carried out in a low-turbulence wind tunnel by means of a hot-wire anemometer in a boundary layer developing over a $25\textdegree $ swept-wing model. The harmonic-in-time free-stream vortices were excited by a thin vibrating wire located upstream of the experimental-model leading edge and represented a kind of small-amplitude von Kármán vortex street with spanwise orientation of the generated instantaneous vorticity vectors. The controlled roughness elements (the so-called ‘phased roughness’) were placed on the model surface. This roughness had a special shape, which provided excitation of CF-waves having basically some predetermined (required) spanwise wavenumbers. The linearity of the stability and receptivity mechanisms under study was checked accurately by means of variation of both the free-stream-vortex amplitude and the surface roughness height. These experiments were directed to obtaining the amplitudes and phases of the vortex-roughness receptivity coefficients for a number of vortex disturbance frequencies. The vortex street position with respect to the model surface (the vortex offset parameter) was also varied. The receptivity characteristics obtained experimentally in Fourier space are independent of the particular roughness shape, and can be used for validation of receptivity theories.

JFM classification

Boundary Layers: Boundary layer receptivity Instability: Instability Instability: Transition to turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 716 , 10 February 2013 , pp. 487 - 527
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bake, S., Borodulin, V. I., Kachanov, Y. S. & Roschektayev, A. P. 2002a Experimental study of 3D localized boundary-layer receptivity to free stream vortices by means of two-source method. In XI International Conference on Methods of Aerophysical Research. Proceedings. Part I, pp. 28–33. Inst. Theor. and Appl. Mech.Google Scholar
Bake, S., Ivanov, A. V., Fernholz, H. H., Neemann, K. & Kachanov, Y. S. 2002b Receptivity of boundary layers to three-dimensional disturbances. Eur. J. Mech. (B/Fluids) 19 (1), 29–48.CrossRefGoogle Scholar
Bertolotti, F. P. 1996 On the birth and evolution of disturbances in three-dimensional boundary layers. In Nonlinear Instability and Transition in Three-Dimensional Boundary Layers (ed. Duck, P. W. & Hall, P.), pp. 247–256. Kluwer.Google Scholar
Bertolotti, F. P. 1997 Response of the Blasius boundary layer to free-stream vorticity. Phys. Fluids 9 (8), 2286–2299.CrossRefGoogle Scholar
Bertolotti, F. P. & Kendall, J. M. 1997 Response of the Blasius boundary layer to controlled free stream vortices of axial form. AIAA Paper 97-2018.CrossRefGoogle Scholar
Boiko, A. V. 2002a Receptivity of a flat plate boundary layer to a free stream axial vortex. Eur. J. Mech. (B/Fluids) 21, 325–340.Google Scholar
Boiko, A. V. 2002b Swept-wing boundary layer receptivity to a steady free stream vortex disturbance. Fluid Dyn. 37 (1), 37–45.CrossRefGoogle Scholar
Borodulin, V. I., Fedenkova, A. A., Ivanov, A. V., Kachanov, Y. S. & Komarova, V. Y. 2005 3D distributed boundary-layer receptivity to non-stationary free-stream vortices in presence of surface roughness. In 21st International Congress of Theoretical and Applied Mechanics. ICTAM Proceedings (Extended Summaries on CD-ROM) (ed. Gutkowski, W. & Kowalewski, T. A.). Springer.Google Scholar
Borodulin, V. I., Gaponenko, V. R., Ivanov, A. V. & Kachanov, Y. S. 1996 Method of introduction of normal instability modes into the 3D boundary layer. In Proceedings of 8th International Conference on Methods of Aerophysical Research. Part 2 (ed. Kharitonov, A. M.), pp. 39–45. Inst. Theor. and Appl. Mech.Google Scholar
Borodulin, V. I., Gaponenko, V. R., Ivanov, A. V. & Kachanov, Y. S. 2002 Experimental study of resonant interactions of instability waves in self-similar boundary layer with an adverse pressure gradient. Part 1. Tuned resonances. J. Turbul. 3 (62), 1–38.Google Scholar
Borodulin, V. I., Gaponenko, V. R., Ivanov, A. V., Kachanov, Y. S. & Crouch, J. D. 2000 Stability of a swept-wing boundary layer to stationary and traveling disturbances. Experiment and theory. In Stability of Flows of Homogeneous and Heterogeneous Fluids (ed. Rudyak, V. Y.), vol. 7, pp. 150–153. Inst. Theor. and Appl. Mech., (in Russian).Google Scholar
Borodulin, V. I., Ivanov, A. V., Kachanov, Y. S. & Fedenkova, A. A. 2004a Distributed boundary-layer receptivity to non-stationary vortical disturbances with wall-normal vorticity in the presence of surface roughness. Thermophys. Aeromech. 11 (3), 355–390.Google Scholar
Borodulin, V. I., Ivanov, A. V., Kachanov, Y. S. & Fedenkova, A. A. 2007 Three-dimensional distributed receptivity of a boundary layer to unsteady vortex disturbances. In XIII International Conference on Methods of Aerophysical Research. Proceedings. Part III, pp. 45–50. Parallel.Google Scholar
Borodulin, V. I., Ivanov, A. V., Kachanov, Y. S. & Komarova, V. Y. 2006 Distributed two-dimensional boundary-layer receptivity to non-stationary vortical disturbances in the presence of surface roughness. Thermophys. Aeromech. 13 (2), 183–208.Google Scholar
Borodulin, V. I., Ivanov, A. V., Kachanov, Y. S. & Roschektayev, A. P. 2008 Excitation of cross-flow instability modes at scattering of free stream vortices on surface roughness. In XIV International Conference on Methods of Aerophysical Research. June 30–July 6, 2008. Proceedings (ed. V. M. Fomin), ITAM SB RAS.Google Scholar
Borodulin, V. I., Kachanov, Y. S., Roschektayev, A. P. & Bake, S. 2004b Experimental study of 3D receptivity of a boundary layer to free stream vortices during their scattering on localized surface vibrations. Thermophys. Aeromech. 11 (2), 185–198.Google Scholar
Bottaro, A. 2010 A receptive boundary layer. J. Fluid Mech. 646, 1–4.Google Scholar
Choudhari, M. 1994 Localized and distributed boundary-layer receptivity to convected unsteady wake in free stream. NASA CR-4578.Google Scholar
Choudhari, M. 1996 Boundary-layer receptivity to three-dimensional unsteady vortical disturbances in free stream. AIAA Paper 96-0181.Google Scholar
Choudhari, M. & Streett, C. L. 1992 A finite Reynolds number approach for the prediction of boundary-layer receptivity in localized regions. Phys. Fluids A 4, 2495–2514.Google Scholar
Crouch, J. D. 1994 Distributed excitation of Tollmien–Schlichting waves by vortical free stream disturbances. Phys. Fluids 6 (1), 217–223.Google Scholar
Crouch, J. D. 1997 Transition prediction and control for airplane applications. AIAA Paper 97-1907.Google Scholar
Crouch, J. D., Gaponenko, V. R., Ivanov, A. V. & Kachanov, Y. S. 1997 Theoretical and experimental comparisons of the stability and receptivity of swept-wing boundary layers. Bull. Am. Phys. Soc. 42, 2174.Google Scholar
Crouch, J. D. & Ng, L. L. 1997 Variable n-factor method for transition prediction in three-dimensional boundary layers. AIAA J. 38 (2), 211–216.Google Scholar
Dietz, A. J. 1999 Local boundary-layer receptivity to a connected free stream disturbances. J. Fluid Mech. 378, 291–317.CrossRefGoogle Scholar
Gaponenko, V. R., Ivanov, A. V. & Kachanov, Y. S. 1995a Experimental study of a swept-wing boundary-layer stability with respect to unsteady disturbances. Thermophys. Aeromech. 2 (4), 287–312.Google Scholar
Gaponenko, V. R., Ivanov, A. V. & Kachanov, Y. S. 1995b Experimental study of cross-flow instability of a swept-wing boundary layer with respect to traveling waves. In Laminar-Turbulent Transition (ed. Kobayashi, R.), pp. 373–380. Springer.Google Scholar
Gaponenko, V. R., Ivanov, A. V. & Kachanov, Y. S. 1996 Experimental study of 3D boundary-layer receptivity to surface vibrations. In IUTAM Symposium on Nonlinear Instability and Transition in Three-Dimensional Boundary Layers (ed. Duck, P. W. & Hall, P.), pp. 389–398. Kluwer.Google Scholar
Gaponenko, V. R., Ivanov, A. V., Kachanov, Y. S. & Crouch, J. D. 2002 Swept-wing boundary-layer receptivity to surface non-uniformities. J. Fluid Mech. 461, 93–126.Google Scholar
Gianetti, F. & Luchini, P. 2006 Leading edge receptivity by adjoint methods. J. Fluid Mech. 547, 21–53.CrossRefGoogle Scholar
Goldstein, M. E. 1983 The evolution of Tollmien–Schlichting waves near a leading edge. J. Fluid Mech. 127, 59–81.Google Scholar
Goldstein, M. E. 1985 Scattering of acoustic waves into Tollmien–Schlichting waves by small streamwise variations in surface geometry. J. Fluid Mech. 154, 509–529.CrossRefGoogle Scholar
Goldstein, M. E. & Leib, S. J. 1993 Three-dimensional boundary layer instability and separation induced by small-amplitude streamwise vorticity in the upstream flow. J. Fluid Mech. 246, 21–41.CrossRefGoogle Scholar
Ivanov, A. V., Kachanov, Y. S. & Koptsev, D. B. 1998 Method of phased roughness for determining the acoustic receptivity coefficients. In IX International Conference on Methods of Aerophysical Research. Proceedings. Part II, pp. 89–94. Inst. Theor. and Appl. Mech.Google Scholar
Ivanov, A. V., Kachanov, Y. S. & Koptsev, D. B. 2001 Excitation of cross-flow instability waves by acoustic field in presence of a surface roughnes. Thermophys. Aeromech. 8 (3), 345–361.Google Scholar
Kachanov, Y. S. 2000 Three-dimensional receptivity of boundary layers. Eur. J. Mech. (B/Fluids) 19 (5), 723–744.Google Scholar
Kachanov, Y. S., Borodulin, V. I., Ivanov, A. V. & Roschektayev, A. P. 2001 a Swept-wing boundary-layer vortex receptivity due to surface non-uniformities. Part 1. External and surface perturbations and evolution of excited cross-flow waves. Tech. Rep. Interim Project Report on Agreement No 106 (Exhibit 106H, Part A), June 2001 Novosibirsk: Inst. Theor. and Appl. Mech.Google Scholar
Kachanov, Y. S., Borodulin, V. I., Ivanov, A. V. & Roschektayev, A. P. 2001 b Swept-wing boundary-layer vortex receptivity due to surface non-uniformities. Part 2. Disturbance spectra and receptivity coefficients. Tech. Rep. Final Project Report on Agreement No 106 (Exhibit 106H, Part A), November 2001 Novosibirsk: Inst. Theor. and Appl. Mech.Google Scholar
Kachanov, Y. S., Kozlov, V. V. & Levchenko, V. Y. 1979a Origin of Tollmien–Schlichting waves in boundary layer under the influence of external disturbances. Fluid Dyn. 13, 704–711.Google Scholar
Kachanov, Y. S., Kozlov, V. V. & Levchenko, V. Ya. 1982 Origin of Turbulence in Boundary Layer. Nauka, (in Russian).Google Scholar
Kachanov, Y. S., Kozlov, V. V., Levchenko, V. Y. & Maksimov, V. P. 1979b Transformation of external disturbances into the boundary layer waves. In Proceedings of Sixth International Conference on Numerical Methods in Fluid Dyn, pp. 299–307. Springer.Google Scholar
Kendall, J. M. 1985 Experimental study of disturbances produced in a pre-transitional laminar boundary layer by weak free stream turbulence. AIAA Paper 85-1695.CrossRefGoogle Scholar
Kendall, J. M. 1990 Boundary-layer receptivity to free stream turbulence. AIAA Paper 90-1504.CrossRefGoogle Scholar
Kendall, J. M. 1991 Studies on laminar boundary-layer receptivity to free stream turbulence near a leading edge. In Boundary Layer Stability and Transition to Turbulence (ed. D. C. Reda, H. L. Reed & R. K. Kobayashi). ASME FED vol. 114, pp. 23–30.Google Scholar
Kerschen, E. J. 1990 Boundary-layer receptivity theory. Appl. Mech. Rev. 43, S152–S157.Google Scholar
Kerschen, E. J. 1991 Linear and non-linear receptivity to vortical free stream disturbances. In Boundary Layer Stability and Transition to Turbulence (ed. D. C. Reda, H. L. Reed & R. K. Kobayashi). ASME FED vol. 114, pp. 43–48.Google Scholar
Kogan, M. N., Shumilkin, V. G., Ustinov, M. V. & Zhigulev, S. G. 2001 Experimental study of flat-plate boundary layer receptivity to vorticity normal to leading edge. Eur. J. Mech. (B/Fluids) 20, 813–820.Google Scholar
Leehey, P. 1980 Influence of environment in laminar boundary layer control. In Viscous Flow Drag Reduction, Progress in Astronautics and Aeronautics (ed. Hough, G. R.), vol. 72, pp. 4–16. AIAA Benjamin.Google Scholar
Leib, S. I., Wundrow, D. W. & Goldstein, M. E. 1999 Effect of free streamturbulence and other vortical disturbances on a laminar boundary layer. J. Fluid Mech. 380, 169–203.CrossRefGoogle Scholar
Mack, L. M. 1975 A numerical method for the prediction of high speed boundary-layer transition using linear theory. NASA SP-347.Google Scholar
Mack, L. M. 1977 Transition. prediction and linear stability theory. AGARD CP-224, Paper 1.Google Scholar
Nishioka, M. & Morkovin, M. V. 1986 Boundary-layer receptivity to unsteady pressure gradients: experiments and overview. J. Fluid Mech. 171, 219–261.Google Scholar
Ricco, P., Luo, J. & Wu, X. 2011 Evolution and instability of unsteady nonlinear streaks generated by free-stream vortical disturbances. J. Fluid Mech. 677, 1–38.Google Scholar
Ricco, P. & Wu, X. 2007 Response of a compressible laminar boundary layer to free stream vortical disturbances. J. Fluid Mech. 587, 97–138.Google Scholar
Rogler, H. L. & Reshotko, E. 1975 Disturbances in a boundary layer introduced by a low intensity array of vortices. SIAM J. Appl. Mech. 28 (2), 431–462.Google Scholar
Ruban, A. I. 1985 On the generation of Tollmien–Schlichting waves by sound. Fluid Dyn. 25 (2), 213–221.Google Scholar
Saric, W., Reed, H. & Kerschen, E. 2002 Boundary-layer receptivity to free stream disturbances. Ann. Rev. Fluid Mech. 34, 291–319.Google Scholar
Schrader, L. U., Amin, S. & Brandt, L. 2010 Transition to turbulence in the boundary layer over a smooth and a rough swept plate exposed to free stream turbulence. J. Fluid Mech. 646, 297–325.Google Scholar
Tempelmann, D. T., Schrader, L. U., Hanifi, A., Brandt, L. & Henningson, D. S. 2011 Numerical study of boundary-layer receptivity on a swept wing. AIAA Paper 2011-3294.Google Scholar
Ustinov, M. V. 2001a Receptivity of a flat plate boundary layer to a free stream axial vortex. Eur. J. Mech. (B/Fluids) 20, 799–812.Google Scholar
Ustinov, M. V. 2001b Receptivity of the swept wing boundary layer to a steady flow inhomogeneity. Fluid Dyn. 36 (3), 437–447.Google Scholar
Ustinov, M. V. 2002 Receptivity of the blunt-leading-edge plate boundary layer to unsteady vortex perturbations. Fluid Dyn. 37 (4), 556–567.Google Scholar
Wu, X. 2001a On local boundary-layer receptivity to vortical disturbances in the free stream. J. Fluid Mech. 449, 373–393.CrossRefGoogle Scholar
Wu, X. S. 2001b Receptivity of boundary layers with distributed roughness to vortical and acoustic disturbances: a second-order asymptotic theory and comparison with experiments. J. Fluid Mech. 431, 91–133.Google Scholar
Wu, X. & Choudhari, M. 2003 Linear and nonlinear instabilities of a Blasius boundary layer perturbed by streamwise vortices. Part 2. Intermittent instability induced by long-wavelength Klebanoff modes. J. Fluid Mech. 483, 249–286.Google Scholar
Wu, X., Zhao, D. & Luo, J. 2011 Excitation of steady and unsteady Görtler vortices by free-stream vortical disturbances. J. Fluid Mech. 682, 66–100.Google Scholar
Würz, W., Herr, S., Wagner, S. & Kachanov, Y. S. 2002 A first experimental approach to the distributed 3D-vortex receptivity of a boundary layer on an airfoil. In XI International Conference on Methods of Aerophysical Research. Proceedings. Part II, pp. 173–178. Inst. Theor. and Appl. Mech.Google Scholar
Würz, W., Herr, S., Wagner, S. & Kachanov, Y. S. 2005 Experimental investigation of 3D acoustic receptivity of an airfoil boundary layer due to surface vibrations. Eur. J. Mech. (B/Fluids) 24 (5), 621–641.Google Scholar
Würz, W., Herr, S., Wörner, A., Rist, U., Wagner, S. & Kachanov, Y. S. 2003 Three-dimensional acoustic-roughness receptivity of a boundary layer on an airfoil: experiment and direct numerical simulations. J. Fluid Mech. 478, 135–163.Google Scholar
Zavol’skii, N. A., Reutov, V. P. & Rybushkina, G. V. 1983 Excitation of Tollmien–Schlichting waves by acoustic and vortex disturbance scattering in boundary layer on a wavy surface. J. Appl. Mech. Tech. Phys. 24, 355–361.Google Scholar
Zhigulev, V. N. & Tumin, A. M. 1987 Onset of turbulence. In Dynamical Theory of Excitation and Development of Instabilities in Boundary Layers. Nauka. Sib. otd., (in Russian).Google Scholar