Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Martinez, Ariana G.
Kuras, Benjamin
Tindaro Migliorino, Mario
Scalo, Carlo
and
Heister, Stephen D.
2021.
Experimental Demonstration of High-Amplitude Thermoacoustic Instabilities Under Transcritical Temperature Conditions In a Standing-Wave Device.
Martinez, Ariana
Migliorino, Mario Tindaro
Scalo, Carlo
and
Heister, Stephen D.
2021.
Experimental and numerical investigation of standing-wave thermoacoustic instability under transcritical temperature conditions.
The Journal of the Acoustical Society of America,
Vol. 150,
Issue. 4,
p.
2900.
Hao, Haitian
Scalo, Carlo
and
Semperlotti, Fabio
2021.
Flexural-mode solid-state thermoacoustics.
Mechanical Systems and Signal Processing,
Vol. 148,
Issue. ,
p.
107143.
Hunt, Steven A.
Migliorino, Mario Tindaro
Scalo, Carlo
and
Heister, Stephen D.
2021.
Onset Criteria for Bulk-Mode Thermoacoustic Instabilities in Supercritical Hydrocarbon Fuels.
Journal of Fluids Engineering,
Vol. 143,
Issue. 4,
Hu, Zhan-Chao
2021.
Pseudo-boiling and concentration gradient in an enclosed supercritical binary mixture.
International Journal of Heat and Mass Transfer,
Vol. 177,
Issue. ,
p.
121544.
Ruggeri, Matteo
Roy, Indradip
Mueterthies, Michael J.
Gruenwald, Tom
and
Scalo, Carlo
2022.
Neural-network-based Riemann solver for real fluids and high explosives; application to computational fluid dynamics.
Physics of Fluids,
Vol. 34,
Issue. 11,
Hao, Haitian
and
Semperlotti, Fabio
2022.
Instabilities of intrinsic thermoacoustic modes in a thermoacoustic waveguide with anechoic terminations.
Physical Review B,
Vol. 106,
Issue. 9,
Di Meglio, Armando
and
Massarotti, Nicola
2022.
CFD Modeling of Thermoacoustic Energy Conversion: A Review.
Energies,
Vol. 15,
Issue. 10,
p.
3806.
Buschhagen, Timo
Gejji, Rohan M.
Scalo, Carlo
and
Slabaugh, Carson D.
2022.
Self-excited instability regimes of a confined turbulent jet flame at elevated pressure.
Physics of Fluids,
Vol. 34,
Issue. 4,
Hu, Zhan-Chao
2022.
Coupled Heat and Mass Transfer in Binary Mixtures at Supercritical Pressures.
p.
49.
Hao, Haitian
Scalo, Carlo
and
Semperlotti, Fabio
2022.
On the use of negative thermal expansion engineered structures in flexural-mode solid-state thermoacoustics.
Journal of Sound and Vibration,
Vol. 538,
Issue. ,
p.
117223.
Huang, Jiale
Yang, Rui
Yang, Yupeng
Zhou, Qiang
and
Luo, Ercang
2023.
Generalized thermoacoustic heat engines with unconventional working substances: A review.
Applied Energy,
Vol. 347,
Issue. ,
p.
121447.
Xiao, Lei
Luo, Kaiqi
Luo, Ercang
and
Xu, Jingyuan
2023.
A Summary: Dynamic and thermodynamic analysis of thermoacoustic and Stirling systems based on time-domain acoustic-electrical analogy.
Applied Energy,
Vol. 347,
Issue. ,
p.
121377.
Wang, Kaixin
and
Hu, Zhan-Chao
2023.
Experimental investigation of a novel standing-wave thermoacoustic engine based on PCHE and supercritical CO2.
Energy,
Vol. 282,
Issue. ,
p.
128334.
Blanc, Nathan
Yang, Rui
Ramon, Guy Z.
and
Luo, Ercang
2023.
Thermoacoustic engines with near-critical working fluids.
Applied Thermal Engineering,
Vol. 231,
Issue. ,
p.
120845.
Zhang, Rui
and
Chen, Lin
2023.
Comparison study of fluid thermal boundary-bulk behaviors in the close-to-critical region under different property trends.
Physics of Fluids,
Vol. 35,
Issue. 8,
Wang, Kaixin
Han, Baolin
Peng, Hui
and
Hu, Zhan-Chao
2024.
Influence of resonator length and temperature configuration on the performance of a supercritical CO2 thermoacoustic engine.
Applied Thermal Engineering,
Vol. 250,
Issue. ,
p.
123462.
Hu, Zhan-Chao
and
Wang, Kaixin
2024.
Effect of channel size on the performance of a PCHE-based supercritical CO2 thermoacoustic engine.
Applied Thermal Engineering,
Vol. 236,
Issue. ,
p.
121457.
Yang, Rui
Yang, Yupeng
Xu, Jingyuan
Wu, Zhanghua
and
Luo, Ercang
2024.
Thermoacoustic refrigeration with compressible liquid as working fluid.
International Journal of Refrigeration,
Vol. 162,
Issue. ,
p.
1.
Wang, Gaoyuan
and
Hu, Zhan-Chao
2025.
Fundamental insights into enhancing supercritical heat transfer via pulsating flow: Interaction between wave and pseudo-interface.
International Journal of Heat and Mass Transfer,
Vol. 236,
Issue. ,
p.
126373.
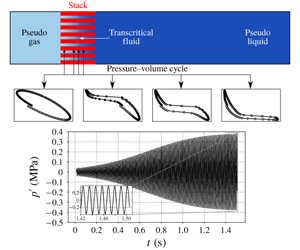
 $\text{CO}_{2}$ in transcritical conditions. The parameter space spans the range of base pressures
$\text{CO}_{2}$ in transcritical conditions. The parameter space spans the range of base pressures  $p_{0}=1.01-1.5\,p_{cr}$ and temperature differences
$p_{0}=1.01-1.5\,p_{cr}$ and temperature differences  $\unicode[STIX]{x0394}T=T_{hot}-T_{cold}$ up to 200 K, with thermodynamic and transport properties obtained from the Peng–Robinson equation of state and Chung’s model. The set-up is a classic standing-wave thermoacoustic resonator, which has been optimized resulting in a minimum temperature difference required to sustain the instability of 23 K. Strong real-fluid effects in the thermoacoustic response in the linear regime are observed: (i) the thermoviscous functions need to depend on the complex eigenvalue (and not just the angular frequency) for linear theory to accurately predict the growth rate observed in the Navier–Stokes simulations, due to a high growth-rate-to-frequency ratio; (ii) the growth rate and frequency vary in a non-monotonic fashion with respect to
$\unicode[STIX]{x0394}T=T_{hot}-T_{cold}$ up to 200 K, with thermodynamic and transport properties obtained from the Peng–Robinson equation of state and Chung’s model. The set-up is a classic standing-wave thermoacoustic resonator, which has been optimized resulting in a minimum temperature difference required to sustain the instability of 23 K. Strong real-fluid effects in the thermoacoustic response in the linear regime are observed: (i) the thermoviscous functions need to depend on the complex eigenvalue (and not just the angular frequency) for linear theory to accurately predict the growth rate observed in the Navier–Stokes simulations, due to a high growth-rate-to-frequency ratio; (ii) the growth rate and frequency vary in a non-monotonic fashion with respect to  $p_{0}$ and
$p_{0}$ and  $\unicode[STIX]{x0394}T$; (iii) the pressure eigenmode amplitude tends to flatten out, and the pressure–velocity phase difference smoothly transitions from
$\unicode[STIX]{x0394}T$; (iii) the pressure eigenmode amplitude tends to flatten out, and the pressure–velocity phase difference smoothly transitions from  $\unicode[STIX]{x03C0}/2$ to
$\unicode[STIX]{x03C0}/2$ to  $-\unicode[STIX]{x03C0}/2$ at the average pressure node location; and (iv) the sharp change in base acoustic impedance at transcritical conditions introduces a discontinuity in the eigenmodes’ spatial derivative. The energy budgets illustrate, for a given
$-\unicode[STIX]{x03C0}/2$ at the average pressure node location; and (iv) the sharp change in base acoustic impedance at transcritical conditions introduces a discontinuity in the eigenmodes’ spatial derivative. The energy budgets illustrate, for a given  $\unicode[STIX]{x0394}T$, the increase of the acoustic power produced, but also of the heat input required, for thermodynamic conditions approaching the critical point. Finally, intense mass transport events at transcritical conditions are shown to entail thermodynamic and convective nonlinearities, which do not, however, govern the limit cycle physics, dominated instead by nonlinear minor losses.
$\unicode[STIX]{x0394}T$, the increase of the acoustic power produced, but also of the heat input required, for thermodynamic conditions approaching the critical point. Finally, intense mass transport events at transcritical conditions are shown to entail thermodynamic and convective nonlinearities, which do not, however, govern the limit cycle physics, dominated instead by nonlinear minor losses.