Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-24T00:12:12.516Z Has data issue: false hasContentIssue false
  • English
  • Français

Rarefaction-driven Rayleigh–Taylor instability. Part 1. Diffuse-interface linear stability measurements and theory

Published online by Cambridge University Press:  15 February 2016

R. V. Morgan ,
O. A. Likhachev  and
J. W. Jacobs
R. V. Morgan*
Affiliation:
Department of Aerospace and Mechanical Engineering, University of Arizona, Tucson, AZ 85721, USA
O. A. Likhachev
Affiliation:
Department of Aerospace and Mechanical Engineering, University of Arizona, Tucson, AZ 85721, USA
J. W. Jacobs
Affiliation:
Department of Aerospace and Mechanical Engineering, University of Arizona, Tucson, AZ 85721, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Theory and experiments are reported that explore the behaviour of the Rayleigh–Taylor instability initiated with a diffuse interface. Experiments are performed in which an interface between two gases of differing density is made unstable by acceleration generated by a rarefaction wave. Well-controlled, diffuse, two-dimensional and three-dimensional, single-mode perturbations are generated by oscillating the gases either side to side, or vertically for the three-dimensional perturbations. The puncturing of a diaphragm separating a vacuum tank beneath the test section generates a rarefaction wave that travels upwards and accelerates the interface downwards. 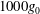This rarefaction wave generates a large, but non-constant, acceleration of the order of $1000g_{0}$, where 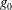$g_{0}$ is the acceleration due to gravity. Initial interface thicknesses are measured using a Rayleigh scattering diagnostic and the instability is visualized using planar laser-induced Mie scattering. Growth rates agree well with theoretical values, and with the inviscid, dynamic diffusion model of Duff et al. (Phys. Fluids, vol. 5, 1962, pp. 417–425) when diffusion thickness is accounted for, and the acceleration is weighted using inviscid Rayleigh–Taylor theory. The linear stability formulation of Chandrasekhar (Proc. Camb. Phil. Soc., vol. 51, 1955, pp. 162–178) is solved numerically with an error function diffusion profile using the Riccati method. This technique exhibits good agreement with the dynamic diffusion model of Duff et al. for small wavenumbers, but produces larger growth rates for large-wavenumber perturbations. Asymptotic analysis shows a 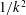$1/k^{2}$ decay in growth rates as 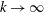$k\rightarrow \infty$ for large-wavenumber perturbations.

JFM classification

Convection: Buoyancy-driven instability Compressible Flows: Gas dynamics Mixing: Turbulent mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 791 , 25 March 2016 , pp. 34 - 60
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bellman, R. & Pennington, R. H. 1954 Effects of surface tension and viscosity on Taylor instability. Q. Appl. Maths 12 (2), 151–162.Google Scholar
Billington, I. J. 1956 An experimental study of the one-dimensional refraction of a rarefaction wave at a contact surface. J. Aero. Sci. 23 (11), 997–1006.Google Scholar
Case, K. M. 1960 Taylor instability of an inverted atmosphere. Phys. Fluids 3 (3), 366–368.Google Scholar
Chandrasekhar, S. 1955 The character of the equilibrium of an incompressible heavy viscous fluid of variable density. Proc. Camb. Phil. Soc. 51 (1), 162–178.CrossRefGoogle Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Oxford University Press.Google Scholar
Chapman, P. R. & Jacobs, J. W. 2006 Experiments on the three-dimensional incompressible Richtmyer–Meshkov instability. Phys. Fluids 18, 074101.Google Scholar
Collins, B. D. & Jacobs, J. W. 2002 PLIF flow visualization and measurements of the Richtmyer–Meshkov instability of an air/ $\text{SF}_{6}$ interface. J. Fluid Mech. 464, 113–136.Google Scholar
Cox, A. J., DeWeerd, A. J. & Linden, J. 2002 An experiment to measure Mie and Rayleigh total scattering cross sections. Am. J. Phys. 70, 620–625.Google Scholar
Drazin, P. G. & Reid, W. H. 1981 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Duff, R. E., Harlow, F. H. & Hirt, C. W. 1962 Effects of diffusion on interface instability between gasses. Phys. Fluids 5, 417–425.Google Scholar
Edwards, M. J., Lindl, J. D., Spears, B. K., Weber, S. V., Atherton, L. J., Bleuel, D. L., Bradley, D. K., Callahan, D. A., Cerjan, C. J., Clark, D. et al. 2011 The experimental plan for cryogenic layered target implosions on the National Ignition Facility – the inertial confinement approach to fusion. Phys. Plasmas 18 (5), 051003.Google Scholar
Emmons, H. W., Chang, C. T. & Watson, B. C. 1960 Taylor instability of finite surface waves. J. Fluid Mech. 7 (2), 177–193.CrossRefGoogle Scholar
Graham, T. 1846 On the motion of gases. Phil. Trans. R. Soc. Lond. 136, 573–631.Google Scholar
Hester, J. J., Stone, J. M., Scowen, P. A., Jun, B. I., Gallagher, J. S., Norman, M. L., Ballester, G. E., Burrows, C. J., Casertano, S., Clarke, J. T. et al. 1996 WFPC2 studies of the Crab Nebula. 3. Magnetic Rayleigh–Taylor instabilities and the origin of the filaments. Astrophys. J. 456 (1), 226–233.CrossRefGoogle Scholar
Hide, R. 1955 Waves in a heavy, viscous, incompressible, electrically conducting fluid of variable density, in the presence of a magnetic field. Proc. R. Soc. Lond. A 233 (1194), 376–396.Google Scholar
Jacobs, J. W. & Krivets, V. V. 2005 Experiments on the late-time development of single-mode Richtmyer–Meshkov instability. Phys. Fluids 17, 034105.Google Scholar
Jones, M. A. & Jacobs, J. W. 1997 A membraneless experiment for the study of Richtmyer–Meshkov instability of a shock-accelerated gas interface. Phys. Fluids 9, 3078–3085.Google Scholar
Lafay, M.-A., LeCreurer, B. & Gauthier, S. 2007 Compressibility effects on the Rayleigh–Taylor instability between miscible fluids. Europhys. Lett. 79 (6), 64002.Google Scholar
Lamb, H. 1932 Hydrodynamics. Cambridge University Press.Google Scholar
LeLevier, R., Lasher, G. J. & Bjorklund, F.1955 Effect of a density gradient on Taylor instability. University of California Radiation Laboratory Report, UCRL-4459.Google Scholar
Lemmon, E. W., Huber, M. L. & McLinden, M. O. 2013 NIST Standard Reference Database 23: Reference Fluid Thermodynamic and Transport Properties – REFPROP, Version 9.1. National Institute of Standards and Technology.Google Scholar
Livescu, D. 2004 Compressibility effects on the Rayleigh–Taylor instability growth between immiscible fluids. Phys. Fluids 16 (1), 118–127.Google Scholar
Menikoff, R. & Zemach, C. 1983 Rayleigh–Taylor instability and the use of conformal maps for ideal fluid flow. J. Comput. Phys. 51, 28–64.Google Scholar
Michioka, H. & Sumita, I. 2005 Rayleigh–Taylor instability of a particle packed viscous fluid: implications for a solidifying magma. Geophys. Res. Lett. 32 (3), L03309.CrossRefGoogle Scholar
Miles, J. W. & Dienes, J. K. 1966 Taylor instability in a viscous liquid. Phys. Fluids 9 (12), 2518–2519.CrossRefGoogle Scholar
Plesset, M. S. & Whipple, C. G. 1974 Viscous effects in Rayleigh–Taylor instability. Phys. Fluids 17 (1), 1–7.Google Scholar
Rayleigh, Lord 1883 Investigation of the character of the equilibrium of an incompressible heavy fluid of variable density. Proc. Lond. Math. Soc. 14, 170–177.Google Scholar
Scott, M. R. 1973 Initial value method for eigenvalue problem for systems of ordinary differential equations. J. Comput. Phys. 12 (3), 334–347.CrossRefGoogle Scholar
Selig, F. 1964 Variational principle for Rayleigh–Taylor instability. Phys. Fluids 7 (8), 1114–1116.CrossRefGoogle Scholar
Sutherland, W. 1895 The viscosity of mixed gases. Phil. Mag. (5) 40, 421–431.CrossRefGoogle Scholar
Taylor, G. I. 1950 The instability of liquid surfaces when accelerated in a direction perpendicular to their planes 1. Proc. R. Soc. Lond. A 201, 192–196.Google Scholar
Town, R. P. J., Delettrez, J. A., Epstein, R., Goncharov, V. N., McCrory, R. L., McKenty, P. W., Short, R. W. & Skupsky, S. 1999 Direct-drive target designs for the National Ignition Facility. LLE Rev. Q. 79, 121–130.Google Scholar
Weber, C. R., Cook, A. W. & Bonazza, R. 2013 Growth rate of a shocked mixing layer with known initial perturbations. J. Fluid Mech. 725, 372–401.CrossRefGoogle Scholar
Wilkinson, J. P. & Jacobs, J. W. 2007 Experimental study of the single-mode three-dimensional Rayleigh–Taylor instability. Phys. Fluids 19, 124102.Google Scholar