Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-22T14:38:42.910Z Has data issue: false hasContentIssue false
  • English
  • Français

Rare transitions to thin-layer turbulent condensates

Published online by Cambridge University Press:  10 September 2019

Adrian van Kan Open the ORCID record for Adrian van Kan [Opens in a new window] ,
Takahiro Nemoto  and
Alexandros Alexakis Open the ORCID record for Alexandros Alexakis [Opens in a new window]
Adrian van Kan*
Affiliation:
Laboratoire de Physique de l’Ecole normale supérieure, ENS, Université PSL, CNRS, Sorbonne Université, Université Paris-Diderot, Sorbonne Paris Cité, 75005 Paris, France
Takahiro Nemoto
Affiliation:
Philippe Meyer Institute for Theoretical Physics, Physics Department, École Normale Supérieure and PSL Research University, 24 rue Lhomond, 75231 Paris CEDEX 05, France
Alexandros Alexakis
Affiliation:
Laboratoire de Physique de l’Ecole normale supérieure, ENS, Université PSL, CNRS, Sorbonne Université, Université Paris-Diderot, Sorbonne Paris Cité, 75005 Paris, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Turbulent flows in a thin layer can develop an inverse energy cascade leading to spectral condensation of energy when the layer height is smaller than a certain threshold. These spectral condensates take the form of large-scale vortices in physical space. Recently, evidence for bistability was found in this system close to the critical height: depending on the initial conditions, the flow is either in a condensate state with most of the energy in the two-dimensional (2-D) large-scale modes, or in a three-dimensional (3-D) flow state with most of the energy in the small-scale modes. This bistable regime is characterised by the statistical properties of random and rare transitions between these two locally stable states. Here, we examine these statistical properties in thin-layer turbulent flows, where the energy is injected by either stochastic or deterministic forcing. To this end, by using a large number of direct numerical simulations (DNS), we measure the decay time 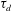$\unicode[STIX]{x1D70F}_{d}$ of the 2-D condensate to 3-D flow state and the build-up time 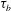$\unicode[STIX]{x1D70F}_{b}$ of the 2-D condensate. We show that both of these times 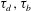$\unicode[STIX]{x1D70F}_{d},\unicode[STIX]{x1D70F}_{b}$ follow an exponential distribution with mean values increasing faster than exponentially as the layer height approaches the threshold. We further show that the dynamics of large-scale kinetic energy may be modelled by a stochastic Langevin equation. From time-series analysis of DNS data, we determine the effective potential that shows two minima corresponding to the 2-D and 3-D states when the layer height is close to the threshold.

JFM classification

Turbulent Flows: Turbulent transition Turbulent Flows: Turbulence simulation Vortex Flows: Vortex breakdown
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 878 , 10 November 2019 , pp. 356 - 369
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alexakis, A. 2011 Two-dimensional behavior of three-dimensional magnetohydrodynamic flow with a strong guiding field. Phys. Rev. E 84 (5), 056330.Google Scholar
Alexakis, A. 2015 Rotating Taylor–Green flow. J. Fluid Mech. 769, 46–78.Google Scholar
Alexakis, A. & Biferale, L. 2018 Cascades and transitions in turbulent flows. Phys. Rep. 767, 1–101.Google Scholar
Allen, R. J., Warren, P. B. & ten Wolde, P. R. 2005 Sampling rare switching events in biochemical networks. Phys. Rev. Lett. 94, 018104.Google Scholar
Avila, K., Moxey, D., de Lozar, A., Avila, M., Barkley, D. & Hof, B. 2011 The onset of turbulence in pipe flow. Science 333 (6039), 192–196.Google Scholar
Benavides, S. J. & Alexakis, A. 2017 Critical transitions in thin layer turbulence. J. Fluid Mech. 822, 364–385.Google Scholar
Billingsley, P. 2008 Probability and Measure. John Wiley & Sons.Google Scholar
Boffetta, G. & Ecke, R. E. 2012 Two-dimensional turbulence. Annu. Rev. Fluid Mech. 44 (1), 427–451.Google Scholar
Bouchet, F., Rolland, J. & Simonnet, E. 2019 Rare event algorithm links transitions in turbulent flows with activated nucleations. Phys. Rev. Lett. 122, 074502.Google Scholar
Celani, A., Musacchio, S. & Vincenzi, D. 2010 Turbulence in more than two and less than three dimensions. Phys. Rev. Lett. 104, 184506.Google Scholar
Cérou, F. & Guyader, A. 2007 Adaptive multilevel splitting for rare event analysis. Stochastic Anal. Appl. 25 (2), 417–443.Google Scholar
Chernykh, A. I. & Stepanov, M. G. 2001 Large negative velocity gradients in burgers turbulence. Phys. Rev. E 64, 026306.Google Scholar
Chertkov, M., Connaughton, C., Kolokolov, I. & Lebedev, V. 2007 Dynamics of energy condensation in two-dimensional turbulence. Phys. Rev. Lett. 99 (8), 084501.Google Scholar
Deusebio, E., Boffetta, G., Lindborg, E. & Musacchio, S. 2014 Dimensional transition in rotating turbulence. Phys. Rev. E 90 (2), 023005.Google Scholar
Donzis, D. A., Yeung, P. K. & Sreenivasan, K. R. 2008 Dissipation and enstrophy in isotropic turbulence: resolution effects and scaling in direct numerical simulations. Phys. Fluids 20 (4), 045108.Google Scholar
Favier, B., Guervilly, C. & Knobloch, E. 2019 Subcritical turbulent condensate in rapidly rotating Rayleigh–Bénard convection. J. Fluid Mech. Google Scholar
Fisher, R. A. & Tippett, L. H. C. 1928 Limiting forms of the frequency distribution of the largest or smallest member of a sample. In Mathematical Proceedings of the Cambridge Philosophical Society, vol. 24, pp. 180–190. Cambridge University Press.Google Scholar
Frisch, U. 1995 Turbulence: The Legacy of AN Kolmogorov. Cambridge University Press.Google Scholar
Gallet, B. & Doering, C. R. 2015 Exact two-dimensionalization of low-magnetic-Reynolds-number flows subject to a strong magnetic field. J. Fluid Mech. 773, 154–177.Google Scholar
Gardiner, C. W. 1986 Handbook of stochastic methods for physics, chemistry and the natural sciences. Appl. Opt. 25, 3145.Google Scholar
Giardinà, C., Kurchan, J. & Peliti, L. 2006 Direct evaluation of large-deviation functions. Phys. Rev. Lett. 96, 120603.Google Scholar
Goldenfeld, N., Guttenberg, N. & Gioia, G. 2010 Extreme fluctuations and the finite lifetime of the turbulent state. Phys. Rev. E 81 (3), 035304.Google Scholar
Goldenfeld, N. & Shih, H.-Y. 2017 Turbulence as a problem in non-equilibrium statistical mechanics. J. Stat. Phys. 167 (3–4), 575–594.Google Scholar
Grafke, T., Grauer, R. & Schäfer, T. 2015a The instanton method and its numerical implementation in fluid mechanics. J. Phys. A 48 (33), 333001.Google Scholar
Grafke, T., Grauer, R., Schäfer, T. & Vanden-Eijnden, E. 2015b Relevance of instantons in Burgers turbulence. Europhys. Lett. 109 (3), 34003.Google Scholar
Grigorio, L. S., Bouchet, F., Pereira, R. M. & Chevillard, L. 2017 Instantons in a Lagrangian model of turbulence. J. Phys. A 50 (5), 055501.Google Scholar
Gumbel, E. J. 1935 Les valeurs extrêmes des distributions statistiques. Ann. Inst. Henri Poincaré 5 (2), 115–158.Google Scholar
Heymann, M. & Vanden-Eijnden, E. 2008 Pathways of maximum likelihood for rare events in nonequilibrium systems: application to nucleation in the presence of shear. Phys. Rev. Lett. 100, 140601.Google Scholar
Hof, B., de Lozar, A., Kuik, D. J. & Westerweel, J. 2008 Repeller or attractor? Selecting the dynamical model for the onset of turbulence in pipe flow. Phys. Rev. Lett. 101 (21), 214501.Google Scholar
Hof, B., Westerweel, J., Schneider, T. M. & Eckhardt, B. 2006 Finite lifetime of turbulence in shear flows. Nature 443 (7107), 59.Google Scholar
Hossain, M., Matthaeus, W. H. & Montgomery, D. 1983 Long-time states of inverse cascades in the presence of a maximum length scale. J. Plasma Phys. 30 (3), 479–493.Google Scholar
van Kan, A. & Alexakis, A. 2019 Condensates in thin-layer turbulence. J. Fluid Mech. 864, 490–518.Google Scholar
Lestang, T., Ragone, F., Br’ehier, C.-E., Herbert, C. & Bouchet, F. 2018 Computing return times or return periods with rare event algorithms. J. Stat. Mech. 2018 (4), 043213.Google Scholar
Marino, R., Mininni, P. D., Rosenberg, D. & Pouquet, A. 2013 Inverse cascades in rotating stratified turbulence: fast growth of large scales. Europhys. Lett. 102 (4), 44006.Google Scholar
Marino, R., Mininni, P. D., Rosenberg, D. L. & Pouquet, A. 2014 Large-scale anisotropy in stably stratified rotating flows. Phys. Rev. E 90 (2), 023018.Google Scholar
Métais, O., Bartello, P., Garnier, E., Riley, J. J. & Lesieur, M. 1996 Inverse cascade in stably stratified rotating turbulence. Dyn. Atmos. Oceans 23 (1–4), 193–203.Google Scholar
Mininni, P. D., Rosenberg, D., Reddy, R. & Pouquet, A. 2011 A hybrid MPI–OpenMP scheme for scalable parallel pseudospectral computations for fluid turbulence. Parallel Comput. 37 (6-7), 316–326.Google Scholar
Musacchio, S. & Boffetta, G. 2017 Split energy cascade in turbulent thin fluid layers. Phys. Fluids 29 (11), 111106.Google Scholar
Musacchio, S. & Boffetta, G. 2019 Condensate in quasi-two-dimensional turbulence. Phys. Rev. Fluids 4 (2), 022602.Google Scholar
Nemoto, T. & Alexakis, A. 2018 Method to measure efficiently rare fluctuations of turbulence intensity for turbulent-laminar transitions in pipe flows. Phys. Rev. E 97, 022207.Google Scholar
Nemoto, T., Bouchet, F., Jack, R. L. & Lecomte, V. 2016 Population-dynamics method with a multicanonical feedback control. Phys. Rev. E 93, 062123.Google Scholar
Pedlosky, J. 2013 Geophysical Fluid Dynamics. Springer.Google Scholar
Pouquet, A., Rosenberg, D., Stawarz, J. E. & Marino, R. 2019 Helicity dynamics, inverse and bi-directional cascades in fluid and MHD turbulence: a brief review. Earth Space Sci. 6 (3), 351–369.Google Scholar
Rubio, A. M., Julien, K., Knobloch, E. & Weiss, J. B. 2014 Upscale energy transfer in three-dimensional rapidly rotating turbulent convection. Phys. Rev. Lett. 112 (14), 144501.Google Scholar
Seshasayanan, K. & Alexakis, A. 2016 Critical behavior in the inverse to forward energy transition in two-dimensional magnetohydrodynamic flow. Phys. Rev. E 93 (1), 013104.Google Scholar
Seshasayanan, K. & Alexakis, A. 2018 Condensates in rotating turbulent flows. J. Fluid Mech. 841, 434–462.Google Scholar
Seshasayanan, K., Benavides, S. J. & Alexakis, A. 2014 On the edge of an inverse cascade. Phys. Rev. E 90 (5), 051003.Google Scholar
Smith, L. M., Chasnov, J. R. & Waleffe, F. 1996 Crossover from two-to three-dimensional turbulence. Phys. Rev. Lett. 77 (12), 2467.Google Scholar
Smith, L. M. & Waleffe, F. 1999 Transfer of energy to two-dimensional large scales in forced, rotating three-dimensional turbulence. Phys. Fluids 11 (6), 1608–1622.Google Scholar
Smith, L. M. & Yakhot, V. 1993 Bose condensation and small-scale structure generation in a random force driven 2D turbulence. Phys. Rev. Lett. 71 (3), 352–355.Google Scholar
Smith, L. M. & Yakhot, V. 1994 Finite-size effects in forced two-dimensional turbulence. J. Fluid Mech. 274, 115–138.Google Scholar
Sozza, A., Boffetta, G., Muratore-Ginanneschi, P. & Musacchio, S. 2015 Dimensional transition of energy cascades in stably stratified forced thin fluid layers. Phys. Fluids 27 (3), 035112.Google Scholar
Tailleur, J. & Kurchan, J. 2007 Probing rare physical trajectories with Lyapunov weighted dynamics. Nat. Phys. 3 (3), 203.Google Scholar
Teo, I., Mayne, C. G., Schulten, K. & Lelivre, T. 2016 Adaptive multilevel splitting method for molecular dynamics calculation of benzamidine-trypsin dissociation time. J. Chem. Theory Comput. 12 (6), 2983–2989.Google Scholar
Xia, H., Byrne, D., Falkovich, G. & Shats, M. 2011 Upscale energy transfer in thick turbulent fluid layers. Nat. Phys. 7 (4), 321.Google Scholar
Xia, H. & Francois, N. 2017 Two-dimensional turbulence in three-dimensional flows. Phys. Fluids 29 (11), 111107.Google Scholar
Yokoyama, N. & Takaoka, M. 2017 Hysteretic transitions between quasi-two-dimensional flow and three-dimensional flow in forced rotating turbulence. Phys. Rev. Fluids 2 (9), 092602.Google Scholar