Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Seadawy, Aly R.
2015.
Fractional solitary wave solutions of the nonlinear higher-order extended KdV equation in a stratified shear flow: Part I.
Computers & Mathematics with Applications,
Vol. 70,
Issue. 4,
p.
345.
Ogden, K. A.
and
Helfrich, Karl R.
2016.
Internal hydraulic jumps in two-layer flows with upstream shear.
Journal of Fluid Mechanics,
Vol. 789,
Issue. ,
p.
64.
Seadawy, Aly R.
2017.
Two-dimensional interaction of a shear flow with a free surface in a stratified fluid and its solitary-wave solutions via mathematical methods.
The European Physical Journal Plus,
Vol. 132,
Issue. 12,
Köhn, Eike E.
Thomsen, Sören
Arévalo-Martínez, Damian L.
and
Kanzow, Torsten
2017.
Submesoscale CO2 variability across an upwelling front off Peru.
Ocean Science,
Vol. 13,
Issue. 6,
p.
1017.
Li, Yanggui
Geng, Xingguo
Liu, Zhijun
Wang, Heping
and
Zang, Duyang
2018.
Simulating Kelvin–Helmholtz instability using dissipative particle dynamics.
Fluid Dynamics Research,
Vol. 50,
Issue. 4,
p.
045512.
MacKinnon, Jennifer A.
Alford, Matthew H.
Voet, Gunnar
Zeiden, Kristin L.
Shaun Johnston, T. M.
Siegelman, Mika
Merrifield, Sophia
and
Merrifield, Mark
2019.
Eddy Wake Generation From Broadband Currents Near Palau.
Journal of Geophysical Research: Oceans,
Vol. 124,
Issue. 7,
p.
4891.
Gualtieri, C.
Ianniruberto, M.
and
Filizola, N.
2019.
On the mixing of rivers with a difference in density: The case of the Negro/Solimões confluence, Brazil.
Journal of Hydrology,
Vol. 578,
Issue. ,
p.
124029.
Johnston, Shaun
Schönau, Martha
Paluszkiewicz, Terri
MacKinnon, Jennifer
Arbic, Brian
Colin, Patrick
Alford, Matthew
Andres, Magdalena
Centurioni, Luca
Graber, Hans
Helfrich, Karl
Hormann, Verena
Lermusiaux, Pierre
Musgrave, Ruth
Powell, Brian
Qiu, Bo
Rudnick, Daniel
Simmons, Harper
St. Laurent, Louis
Terrill, Eric
Trossman, David
Voet, Gunner
Wijesekera, Hemantha
and
Zeiden, Kristin
2019.
FLEAT: A Multiscale Observational and Modeling Program to Understand How Topography Affects Flows in the Western North Pacific.
Oceanography,
Vol. 32,
Issue. 4,
p.
10.
Ogden, Kelly A.
and
Helfrich, Karl
2020.
Internal hydraulic jumps in two-layer flows with increasing upstream shear.
Physical Review Fluids,
Vol. 5,
Issue. 7,
Pouchoulin, S.
Le Coz, J.
Mignot, E.
Gond, L.
and
Riviere, N.
2020.
Predicting Transverse Mixing Efficiency Downstream of a River Confluence.
Water Resources Research,
Vol. 56,
Issue. 10,
Cheng, Yu‐Hsin
Chang, Ming‐Huei
Ko, Dong S.
Jan, Sen
Andres, Magdalena
Kirincich, Anthony
Yang, Yiing Jang
and
Tai, Jen‐Hua
2020.
Submesoscale Eddy and Frontal Instabilities in the Kuroshio Interacting With a Cape South of Taiwan.
Journal of Geophysical Research: Oceans,
Vol. 125,
Issue. 5,
Haney, Sean R.
Simpson, Alexandra J.
McSweeney, Jacqueline M.
Waterhouse, Amy F.
Haller, Merrick C.
Lerczak, James A.
Barth, John A.
Lenain, Luc
Palóczy, André
Adams, Kate
and
MacKinnon, Jennifer A.
2021.
Lifecycle of a Submesoscale Front Birthed from a Nearshore Internal Bore.
Journal of Physical Oceanography,
Vol. 51,
Issue. 11,
p.
3477.
Nagai, Takeyoshi
Hasegawa, Daisuke
Tsutsumi, Eisuke
Nakamura, Hirohiko
Nishina, Ayako
Senjyu, Tomoharu
Endoh, Takahiro
Matsuno, Takeshi
Inoue, Ryuichiro
and
Tandon, Amit
2021.
The Kuroshio flowing over seamounts and associated submesoscale flows drive 100-km-wide 100-1000-fold enhancement of turbulence.
Communications Earth & Environment,
Vol. 2,
Issue. 1,
Althobaiti, Ali
Althobaiti, Saad
El-Rashidy, K.
and
Seadawy, Aly R.
2021.
Exact solutions for the nonlinear extended KdV equation in a stratified shear flow using modified exponential rational method.
Results in Physics,
Vol. 29,
Issue. ,
p.
104723.
Bahmanpouri, Farhad
Barbetta, Silvia
Gualtieri, Carlo
Ianniruberto, Marco
Filizola, Naziano
Termini, Donatella
and
Moramarco, Tommaso
2022.
Prediction of river discharges at confluences based on Entropy theory and surface-velocity measurements.
Journal of Hydrology,
Vol. 606,
Issue. ,
p.
127404.
Johnston, T. M. Shaun
2022.
Stirring and Mixing in the Wake of Angaur and Peleliu Islands, Palau.
Journal of Geophysical Research: Oceans,
Vol. 127,
Issue. 5,
Simpson, Alexandra J.
Shi, Fengyan
Jurisa, Joseph T.
Honegger, David A.
Hsu, Tian‐Jian
and
Haller, Merrick C.
2022.
Observations and Modeling of a Buoyant Plume Exiting Into a Tidal Cross‐Flow and Exhibiting Along‐Front Instabilities.
Journal of Geophysical Research: Oceans,
Vol. 127,
Issue. 2,
Duguay, J.
Biron, P. M.
and
Lacey, J.
2022.
Impact of Density Gradients on the Secondary Flow Structure of a River Confluence.
Water Resources Research,
Vol. 58,
Issue. 10,
Johnston, T. M. Shaun
and
Colin, Patrick L.
2022.
Upwelling and Downwelling Driven by the North Equatorial Countercurrent and Internal Waves at Hatohobei Island and Helen Reef, Palau.
Journal of Geophysical Research: Oceans,
Vol. 127,
Issue. 2,
Osadchiev, Alexander
Gordey, Alexandra
Barymova, Alexandra
Sedakov, Roman
Rogozhin, Vladimir
Zhiba, Roman
and
Dbar, Roman
2022.
Lateral Border of a Small River Plume: Salinity Structure, Instabilities and Mass Transport.
Remote Sensing,
Vol. 14,
Issue. 15,
p.
3818.
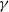 $\gamma $ (where the limits
$\gamma $ (where the limits 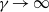 $\gamma \rightarrow \infty $ and
$\gamma \rightarrow \infty $ and 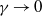 $\gamma \rightarrow 0$ represent a pure gravity current and a pure mixing layer, respectively). The growth rate of three-dimensional instability and the mixing increase for smaller
$\gamma \rightarrow 0$ represent a pure gravity current and a pure mixing layer, respectively). The growth rate of three-dimensional instability and the mixing increase for smaller 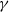 $\gamma $. When
$\gamma $. When 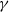 $\gamma $ is sufficiently small, there are two distinct regimes: an early period of during which the interface grows rapidly, followed by horizontal diffusive growth. Numerical results are consistent with field observations of tidal separation flows in the Haro Strait (Farmer, Pawlowicz & Jiang, Dyn. Atmos. Oceans., vol. 36, 2002, pp. 43–58), including the magnitude of downwelling vertical currents, horizontal scales of surface vortex features and mixing rate.
$\gamma $ is sufficiently small, there are two distinct regimes: an early period of during which the interface grows rapidly, followed by horizontal diffusive growth. Numerical results are consistent with field observations of tidal separation flows in the Haro Strait (Farmer, Pawlowicz & Jiang, Dyn. Atmos. Oceans., vol. 36, 2002, pp. 43–58), including the magnitude of downwelling vertical currents, horizontal scales of surface vortex features and mixing rate.