Article contents
Rain-induced attenuation of deep-water waves
Published online by Cambridge University Press: 29 April 2013
Abstract
A laboratory investigation has been undertaken to quantify water wave attenuation rates as a function of rainfall rate. Vertical artificial rainfall is shown to generate weak near-surface velocity fluctuations that decline systematically away from the free surface and are independent of rainfall rate across the range of rainfall rates investigated (40–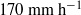 $170~\mathrm{mm} ~{\mathrm{h} }^{- 1} $). In the absence of rain, the observed attenuation of gravity waves is at levels consistent with classical viscous theory, but with a systematic finite-amplitude effect observed above a mean steepness of 0.10. Wave attenuation rates were found to be independent of the mean wave steepness and identical when artificial rainfall rates of 108 and
$170~\mathrm{mm} ~{\mathrm{h} }^{- 1} $). In the absence of rain, the observed attenuation of gravity waves is at levels consistent with classical viscous theory, but with a systematic finite-amplitude effect observed above a mean steepness of 0.10. Wave attenuation rates were found to be independent of the mean wave steepness and identical when artificial rainfall rates of 108 and  $141~\mathrm{mm} ~{\mathrm{h} }^{- 1} $ were applied. Reassessment of complementary theoretical and experimental studies of individual droplets impacting on undisturbed water surfaces indicates that above a weak threshold rainfall rate of
$141~\mathrm{mm} ~{\mathrm{h} }^{- 1} $ were applied. Reassessment of complementary theoretical and experimental studies of individual droplets impacting on undisturbed water surfaces indicates that above a weak threshold rainfall rate of 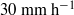 $30~\mathrm{mm} ~{\mathrm{h} }^{- 1} $, the surface irradiation becomes so frequent that droplet-generated violent surface motions directly interact with the incoming droplets. Present evidence is that a matching of time scales develops between the incoming surface irradiation and surface water motions generated by antecedent droplets as the rainfall rate increases. Consequently, at high rainfall rates, a highly dissipative surface regime is created that transmits little of the incident rainfall kinetic energy to the aqueous layers below. Rainfall-induced wave attenuation rates are compared with measurements of other wave attenuation processes to obtain a hierarchy of strength in both the laboratory and the field. Comparison is also made with wave attenuation theories that incorporate momentum and energy flux considerations. Rain-induced wave attenuation rates are weak or very strong depending on whether they are expressed in terms of energy scaling obtained from above or below the surface respectively, due to the high dissipation rate that occurs in the vicinity of the interface.
$30~\mathrm{mm} ~{\mathrm{h} }^{- 1} $, the surface irradiation becomes so frequent that droplet-generated violent surface motions directly interact with the incoming droplets. Present evidence is that a matching of time scales develops between the incoming surface irradiation and surface water motions generated by antecedent droplets as the rainfall rate increases. Consequently, at high rainfall rates, a highly dissipative surface regime is created that transmits little of the incident rainfall kinetic energy to the aqueous layers below. Rainfall-induced wave attenuation rates are compared with measurements of other wave attenuation processes to obtain a hierarchy of strength in both the laboratory and the field. Comparison is also made with wave attenuation theories that incorporate momentum and energy flux considerations. Rain-induced wave attenuation rates are weak or very strong depending on whether they are expressed in terms of energy scaling obtained from above or below the surface respectively, due to the high dissipation rate that occurs in the vicinity of the interface.
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 15
- Cited by


