Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-23T03:19:04.071Z Has data issue: false hasContentIssue false
  • English
  • Français

Quantifying the non-equilibrium characteristics of heterogeneous gas–solid flow of smooth, inelastic spheres using a computational fluid dynamics–discrete element method

Published online by Cambridge University Press:  18 March 2019

Jing Wang ,
Xizhong Chen ,
Wei Bian ,
Bidan Zhao  and
Junwu Wang Open the ORCID record for Junwu Wang [Opens in a new window]
Jing Wang
Affiliation:
State Key Laboratory of Multiphase Complex Systems, Institute of Process Engineering, Chinese Academy of Sciences, P. O. Box 353, Beijing 100190, PR China School of Chemical Engineering, University of Chinese Academy of Sciences, Beijing, 100049, PR China
Xizhong Chen
Affiliation:
State Key Laboratory of Multiphase Complex Systems, Institute of Process Engineering, Chinese Academy of Sciences, P. O. Box 353, Beijing 100190, PR China School of Chemical Engineering, University of Chinese Academy of Sciences, Beijing, 100049, PR China
Wei Bian
Affiliation:
State Key Laboratory of Multiphase Complex Systems, Institute of Process Engineering, Chinese Academy of Sciences, P. O. Box 353, Beijing 100190, PR China School of Chemical Engineering, University of Chinese Academy of Sciences, Beijing, 100049, PR China
Bidan Zhao
Affiliation:
State Key Laboratory of Multiphase Complex Systems, Institute of Process Engineering, Chinese Academy of Sciences, P. O. Box 353, Beijing 100190, PR China School of Chemical Engineering, University of Chinese Academy of Sciences, Beijing, 100049, PR China
Junwu Wang*
Affiliation:
State Key Laboratory of Multiphase Complex Systems, Institute of Process Engineering, Chinese Academy of Sciences, P. O. Box 353, Beijing 100190, PR China School of Chemical Engineering, University of Chinese Academy of Sciences, Beijing, 100049, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Continuum modelling of dense gas–solid flows strongly depends on the constitutive relations used, including the interphase drag force, particle phase stress and the boundary condition for particle–wall interactions. The lack of scale separation is usually claimed to cause the breakdown of the Navier–Stokes (NS) order continuum theory. In this study, computational fluid dynamics–discrete element method (CFD-DEM) simulations of bubbling, turbulent and fast fluidization of smooth, inelastic spheres were conducted to systematically analyse the valid range of NS theory. 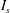An entropy-based criterion $I_{s}$ and Knudsen numbers defined using different characteristic length scales (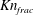$Kn_{frac}$, 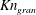$Kn_{gran}$ and 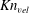$Kn_{vel}$) were quantified. It was found that (i) except at the centre of bubbles where the solid concentration is quite low, NS theory for discrete particles was valid for bubbling fluidization irrespective of the breakdown criterion. Even at the boundary of the bubbles, values of 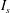$I_{s}$ and 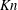$Kn$ were small; and (ii) the conclusion depended on the criterion used in turbulent and fast fluidization. If 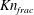$Kn_{frac}$ was used, NS theory would be generally valid. If 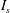$I_{s}$ was chosen, NS theory would be still valid but with lower confidence. However, if 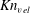$Kn_{vel}$ or 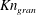$Kn_{gran}$ was selected, NS theory broke down. Because 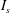$I_{s}$ includes the non-equilibrium effects caused by the gradient of hydrodynamic fields and particle inelasticity, we may conclude that NS theory was valid for all tested cases. This means that the continuum description of discrete particles is not the main source of the breakdown of NS theory.

JFM classification

Multiphase and Particle-laden Flows: Fluidized beds Granular media: Granular media Multiphase and Particle-laden Flows: Particle/fluid flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 866 , 10 May 2019 , pp. 776 - 790
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agrawal, K., Loezos, P. N., Syamlal, M. & Sundaresan, S. 2001 The role of meso-scale structures in rapid gas–solid flows. J. Fluid Mech. 445, 151–185.Google Scholar
Anderson, T. B. & Jackson, R. 1967 Fluid mechanical description of fluidized beds. Equations of motion. Ind. Engng Chem. Fundam. 6 (4), 527–539.Google Scholar
Beetstra, R., van der Hoef, M. A. & Kuipers, J. A. M. 2007 Drag force of intermediate Reynolds number flow past mono- and bidisperse arrays of spheres. AIChE J. 53 (2), 489–501.Google Scholar
Boyd, I. D., Chen, G. & Candler, G. V. 1995 Predicting failure of the continuum fluid equations in transitional hypersonic flows. Phys. Fluids 7 (1), 210–219.Google Scholar
Camberos, J. & Chen, P. H.2003 Continuum breakdown parameter based on entropy generation rates. In 41st AIAA Aerospace Sciences Meeting and Exhibits, Reno, Nevada, AIAA Paper 2003–157.Google Scholar
Carr, R. W., Branam, R. D. & Camberos, J. A.2007 Quantifying non-equilibrium using entropy generation. In 45th AIAA Aerospace Sciences Meeting and Exhibits, Reno, Nevada, AIAA Paper 2007–1127.Google Scholar
Chapman, S. & Cowling, T. G. 1970 The Mathematical Theory of Non-uniform Gases: An Account of the Kinetic Theory of Viscosity, Thermal Conduction and Diffusion in Gases. Cambridge University Press.Google Scholar
Chen, X. & Wang, J. 2017 Dynamic multiscale method for gas–solid flow via spatiotemporal coupling of two-fluid model and discrete particle model. AIChE J. 63, 3681–3691.Google Scholar
Chen, X. & Wang, J. 2018 Mesoscale-structure-based dynamic multiscale method for gas–solid flow. Chem. Engng Sci. 192, 864–881.Google Scholar
Cundall, P. A. & Strack, O. D. L. 1979 A discrete numerical mode for granular assemblies. Géotechnique 29 (1), 47–65.Google Scholar
De Groot, S. R. & Mazur, P. 1984 Non-equilibrium Thermodynamics. Dover Press.Google Scholar
Feng, Y. & Yu, A. 2010 Effect of bed thickness on the segregation behavior of particle mixtures in a gas fluidized bed. Ind. Engng Chem. Res. 49 (7), 3459–3468.Google Scholar
Fullmer, W. D. & Hrenya, C. M. 2016 Quantitative assessment of fine-grid kinetic-theory-based predictions of mean-slip in unbounded fluidization. AIChE J. 62 (1), 11–17.Google Scholar
Fullmer, W. D., Liu, G., Yin, X. & Hrenya, C. M. 2017 Clustering instabilities in sedimenting fluid-solid systems: critical assesment of kinetic-theory-based predictions using direct numerical simulation data. J. Fluid Mech. 823, 433–469.Google Scholar
Gidaspow, D. 1994 Multiphase Flow and Fluidization: Continuum and Kinetic Theory Descriptions. Academic Press.Google Scholar
Hansen, J. S., Dyre, J. C., Daivis, P., Todd, B. D. & Bruus, H. 2015 Continuum nanofluidics. Langmuir 31 (49), 13275–13289.Google Scholar
Hoef, M. A. V. D., Ye, M., Annaland, M. V. S., Andrews, A. T., Sundaresan, S. & Kuipers, J. A. M. 2006 Multiscale modeling of gas-fluidized beds. Adv. Chem. Engng 31 (06), 65–149.Google Scholar
Hrenya, C., Galvin, J. & Wildman, R. 2008 Evidence of higher-order effects in thermally driven rapid granular flows. J. Fluid Mech. 598, 429–450.Google Scholar
Igci, Y., Andrews, A. T., Sundaresan, S., Pannala, S. & O’Brien, T. 2008 Filtered two-fluid models for fluidized gas–particle suspensions. AIChE J. 54 (6), 1431–1448.Google Scholar
Johnson, P. C. & Jackson, R. 1987 Frictional–collisional constitutive relations for granular materials, with application to plane shearing. J. Fluid Mech. 176, 67–93.Google Scholar
Li, J. & Kwauk, M. 1994 Particle-fluid Two-phase Flow: The Energy-minimization Multi-scale Method. Metallurgical Industry Press.Google Scholar
Lockerby, D. A., Reese, J. M. & Struchtrup, H. 2009 Switching criteria for hybrid rarefied gas flow solvers. Proc. R. Soc. Lond. A 465, 1581–1598.Google Scholar
Lu, L., Liu, X., Li, T., Wang, L. & Ge, W.2018 Corrigendum to Assessing the capability of continuum and discrete particle methods to simulate gas-solids flow using DNS predictions as a benchmark [2017 Powder Technol. 321, pp. 301–309] Powder Technol. doi:10.1016/j.powtec.2018.10.055.Google Scholar
Lu, L., Liu, X., Li, T., Wang, L., Ge, W. & Benyahia, S. 2017 Assessing the capability of continuum and discrete particle methods to simulate gas–solids flow using DNS predictions as a benchmark. Powder Technol. 321, 301–309.Google Scholar
Mitrano, P. P., Dahl, S. R., Cromer, D. J., Pacella, M. S. & Hrenya, C. M. 2011 Instabilities in the homogeneous cooling of a granular gas: a quantitative assessment of kinetic-theory predictions. Phys. Fluids 23 (9), 093303.Google Scholar
Mitrano, P. P., Garzó, V., Hilger, A. M., Ewasko, C. J. & Hrenya, C. M. 2012 Assessing a hydrodynamic description for instabilities in highly dissipative, freely cooling granular gases. Phys. Rev. E 85, 041303.Google Scholar
Mitrano, P. P., Zenk, J. R., Sofiane, B., Galvin, J. E., Dahl, S. R. & Hrenya, C. M. 2014 Kinetic-theory predictions of clustering instabilities in granular flows: beyond the small-Knudsen-number regime. J. Fluid Mech. 738, R2.Google Scholar
Müller, C. R., Holland, D. J., Sederman, A. J., Scott, S. A., Dennis, J. S. & Gladden, L. F. 2008 Granular temperature: comparison of magnetic resonance measurements with discrete element model simulations. Powder Technol. 184 (2), 241–253.Google Scholar
Niazmand, H., Mohammadzadeh, A. & Roohi, E. 2013 Predicting continuum breakdown of rarefied micro/nano flows using entropy and entropy generation analysis. Intl J. Mod. Phys. C 24 (05), 1350029.Google Scholar
Pöschel, T. & Schwager, T. 2005 Computational Granular Dynamics: Models and Algorithms. Springer Science & Business Media.Google Scholar
Radl, S. & Sundaresan, S. 2014 A drag model for filtered Euler–Lagrange simulations of clustered gas–particle suspensions. Chem. Engng Sci. 117, 416–425.Google Scholar
Rao, K. K. & Nott, P. R. 2008 An Introduction to Granular Flow. Cambridge University Press.Google Scholar
Sela, N. & Goldhirsch, I. 1998 Hydrodynamic equations for rapid flows of smooth inelastic spheres, to Burnett order. J. Fluid Mech. 361, 41–74.Google Scholar
Tan, M. & Goldhirsch, I. 1998 Rapid granular flows as mesoscopic systems. Phys. Rev. Lett. 81 (14), 3022–3025.Google Scholar
Tsuji, Y., Kawaguchi, T. & Tanaka, T. 1993 Discrete particle simulation of two-dimensional fluidized bed. Powder Technol. 77 (1), 79–87.Google Scholar
Van der Hoef, M., van Sint Annaland, M., Deen, N. & Kuipers, J. 2008 Numerical simulation of dense gas–solid fluidized beds: a multiscale modeling strategy. Annu. Rev. Fluid Mech. 40, 47–70.Google Scholar
Wang, J. 2008 High-resolution Eulerian simulation of RMS of solid volume fraction fluctuation and particle clustering characteristics in a CFB riser. Chem. Engng Sci. 63, 3341–3347.Google Scholar
Wang, J., Ge, W. & Li, J. 2008 Eulerian simulation of heterogeneous gas–solid flows in CFB risers: EMMS-based sub-grid scale model with a revised cluster description. Chem. Engng Sci. 63 (6), 1553–1571.Google Scholar
Wang, J., Van der Hoef, M. & Kuipers, J. 2009 Why the two-fluid model fails to predict the bed expansion characteristics of Geldart A particles in gas-fluidized beds: a tentative answer. Chem. Engng Sci. 64 (3), 622–625.Google Scholar
Wang, J., Van der Hoef, M. & Kuipers, J. 2010 CFD study of the minimum bubbling velocity of Geldart A particles in gas-fluidized beds. Chem. Engng Sci. 65 (12), 3772–3785.Google Scholar
Yang, N., Wang, W., Ge, W. & Li, J. 2003 CFD simulation of concurrent-up gas–solid flow in circulating fluidized beds with structure–dependent drag coefficient. Chem. Engng J. 96 (1), 71–80.Google Scholar
Zhao, B., Wang, J. & Wang, J. 2017 An entropy criterion for the validity of Navier–Stokes order continuum theory for gas–solid flow: kinetic theory analysis. Chem. Engng Sci. 172, 297–309.Google Scholar