Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-28T17:17:06.693Z Has data issue: false hasContentIssue false
  • English
  • Français

Quantifying eddy structures and very-large-scale motions in turbulent round jets

Published online by Cambridge University Press:  06 April 2021

Milad Samie Open the ORCID record for Milad Samie [Opens in a new window] ,
Philippe Lavoie  and
Andrew Pollard
Milad Samie
Affiliation:
Department of Mechanical and Materials Engineering, Queen's University, Kingston, ONK7L 3N6, Canada
Philippe Lavoie*
Affiliation:
Institute for Aerospace Studies, University of Toronto, Toronto, ONM3H 5T6, Canada
Andrew Pollard
Affiliation:
Department of Mechanical and Materials Engineering, Queen's University, Kingston, ONK7L 3N6, Canada
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

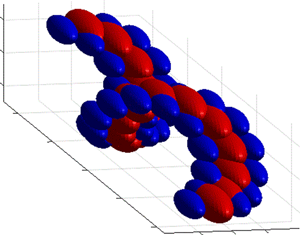
Coherent structures in turbulent round jets are evaluated for a jet Reynolds number up to $Re_d=50\,000$ with the aid of two-point measurements and an existing direct numerical simulation (DNS) dataset at $Re_d=7290$. The experimental data comprise simultaneous velocity time series acquired with both radial and azimuthal separations between the sensors. A spectral correlation analysis is applied to these data that reveals that the coherent structures in the jet flow consist of two principal configurations, which correspond to two main spectral domains. One spectral domain, which is signified by small to medium wavelengths, is associated with hierarchical eddy structures (ESs) for which a physical aspect ratio of $1.2:1:1$ in the axial, radial and azimuthal directions is observed. The other spectral domain, indicated by large wavelengths, is associated with very-large-scale motions (VLSMs). The wavelength marking the boundary between these spectral domains is used to decompose the velocity fluctuations into ES and VLSM components, and the corresponding ES and VLSM components of two-point correlations are obtained from the experimental data. The VLSM component of two-point correlations denotes helical structures as the dominant VLSMs in the jet turbulent region. Instantaneous axial velocity fluctuation fields from DNS support the prevalence of helical VLSMs in the jet. Moreover, the ES signatures are evident in the unwrapped axial–azimuthal planes of the DNS, indicating that the VLSMs are formed by the concatenation of ESs. Consistent with the experimental two-point correlations and DNS flow fields, a conceptual model is proposed for the ESs and VLSMs, which illustrates their arrangements.

JFM classification

Wakes/Jets: Jets
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 916 , 10 June 2021 , A2
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Adrian, R.J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19 (4), 041301.CrossRefGoogle Scholar
Adrian, R.J., Meinhart, C.D. & Tomkins, C.D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.CrossRefGoogle Scholar
Anghan, C., Dave, S., Saincher, S. & Banerjee, J. 2019 Direct numerical simulation of transitional and turbulent round jets: evolution of vortical structures and turbulence budget. Phys. Fluids 31 (6), 065105.CrossRefGoogle Scholar
Baars, W.J., Hutchins, N. & Marusic, I. 2016 Spectral stochastic estimation of high-Reynolds-number wall-bounded turbulence for a refined inner-outer interaction model. Phys. Rev. Fluids 1 (5), 054406.CrossRefGoogle Scholar
Baars, W.J., Hutchins, N. & Marusic, I. 2017 Self-similarity of wall-attached turbulence in boundary layers. J. Fluid Mech. 823, R2.CrossRefGoogle Scholar
Baars, W.J. & Marusic, I. 2020 Data-driven decomposition of the streamwise turbulence kinetic energy in boundary layers. Part 1. Energy spectra. J. Fluid Mech. 882, A25.CrossRefGoogle Scholar
Baidya, R., et al. 2019 Simultaneous skin friction and velocity measurements in high Reynolds number pipe and boundary layer flows. J. Fluid Mech. 871, 377–400.CrossRefGoogle Scholar
Bailey, S.C.C., Hultmark, M., Smits, A.J. & Schultz, M.P. 2008 Azimuthal structure of turbulence in high Reynolds number pipe flow. J. Fluid Mech. 615, 121–138.CrossRefGoogle Scholar
Balakumar, B.J. & Adrian, R.J. 2007 Large-and very-large-scale motions in channel and boundary-layer flows. Phil. Trans. R. Soc. A 365 (1852), 665–681.CrossRefGoogle ScholarPubMed
Ball, C.G., Fellouah, H. & Pollard, A. 2012 The flow field in turbulent round free jets. Prog. Aerosp. Sci. 50, 1–26.CrossRefGoogle Scholar
Baltzer, J.R., Adrian, R.J. & Wu, X. 2013 Structural organization of large and very large scales in turbulent pipe flow simulation. J. Fluid Mech. 720, 236.CrossRefGoogle Scholar
Bendat, J.S. & Piersol, A.G. 2011 Random Data: Analysis and Measurement Procedures. John Wiley & Sons.Google Scholar
Breda, M. & Buxton, O.R.H. 2018 Influence of coherent structures on the evolution of an axisymmetric turbulent jet. Phys. Fluids 30 (3), 035109.CrossRefGoogle Scholar
Browand, F.K. & Laufer, J. 1975 The roles of large scale structures in the initial development of circular jets. In Symposia on Turbulence in Liquids, p. 35. University of Missouri–Rolla.Google Scholar
Casey, T.A., Sakakibara, J. & Thoroddsen, S.T. 2013 Scanning tomographic particle image velocimetry applied to a turbulent jet. Phys. Fluids 25 (2), 025102.CrossRefGoogle Scholar
Cavalieri, A.V.G., Rodríguez, D., Jordan, P., Colonius, T. & Gervais, Y. 2013 Wavepackets in the velocity field of turbulent jets. J. Fluid Mech. 730, 559–592.CrossRefGoogle Scholar
Crow, S.C. & Champagne, F.H. 1971 Orderly structure in jet turbulence. J. Fluid Mech. 48, 547–591.CrossRefGoogle Scholar
Delville, J., Ukeiley, L., Cordier, L., Bonnet, J. & Glauser, M. 1999 Examination of large-scale structures in a turbulent plane mixing layer. Part 1. Proper orthogonal decomposition. J. Fluid Mech. 391, 91–122.CrossRefGoogle Scholar
Dimotakis, P.E., Miake-Lye, R.C. & Papantoniou, D.A. 1983 Structure and dynamics of round turbulent jets. Phys. Fluids 26 (11), 3185–3192.CrossRefGoogle Scholar
Fellouah, H., Ball, C.G. & Pollard, A. 2009 Reynolds number effects within the development region of a turbulent round free jet. Intl J Heat Mass Transfer 52 (17–18), 3943–3954.CrossRefGoogle Scholar
Fiedler, H.E. 1988 Coherent structures in turbulent flows. Prog. Aerosp. Sci. 25 (3), 231–269.CrossRefGoogle Scholar
Fu, Z., Agarwal, A., Cavalieri, A.V.G., Jordan, P. & Brès, G.A. 2017 Turbulent jet noise in the absence of coherent structures. Phys. Rev. Fluids 2 (6), 064601.CrossRefGoogle Scholar
Glauser, M.N., Leib, S.J. & George, W.K. 1987 Coherent structures in the axisymmetric turbulent jet mixing layer. In Turbulent Shear Flows 5, pp. 134–145. Springer.CrossRefGoogle Scholar
Guala, M., Hommema, S.E. & Adrian, R.J. 2006 Large-scale and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 554, 521.CrossRefGoogle Scholar
Head, M.R. & Bandyopadhyay, P. 1981 New aspects of turbulent boundary-layer structure. J. Fluid Mech. 107, 297–338.CrossRefGoogle Scholar
Hussain, A.K.M.F. 1983 Coherent structures—reality and myth. Phys. Fluids 26 (10), 2816–2850.CrossRefGoogle Scholar
Hussain, A.K.M.F. 1986 Coherent structures and turbulence. J. Fluid Mech. 173, 303–356.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.CrossRefGoogle Scholar
Hutchins, N., Monty, J.P., Ganapathisubramani, B., Ng, H.C. & Marusic, I. 2011 Three-dimensional conditional structure of a high-Reynolds-number turbulent boundary layer. J. Fluid Mech. 673, 255.CrossRefGoogle Scholar
Jung, D., Gamard, S. & George, W.K. 2004 Downstream evolution of the most energetic modes in a turbulent axisymmetric jet at high Reynolds number. Part 1. The near-field region. J. Fluid Mech. 514, 173–204.CrossRefGoogle Scholar
Lee, J.H. & Sung, H.J. 2011 Very-large-scale motions in a turbulent boundary layer. J. Fluid Mech. 673, 80–120.CrossRefGoogle Scholar
Lee, J.H., Sung, H.J. & Adrian, R.J. 2019 Space–time formation of very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 881, 1010–1047.CrossRefGoogle Scholar
Liepmann, D. & Gharib, M. 1992 The role of streamwise vorticity in the near-field entrainment of round jets. J. Fluid Mech. 245, 643–668.CrossRefGoogle Scholar
Ligrani, P.M. & Bradshaw, P. 1987 Subminiature hot-wire sensors: development and use. J. Phys. E 20 (3), 323.CrossRefGoogle Scholar
Mankbadi, R. & Liu, J.T.C. 1984 Sound generated aerodynamically revisited: large-scale structures in a turbulent jet as a source of sound. Phil. Trans. R. Soc. Lond. A 311 (1516), 183–217.Google Scholar
Marusic, I. & Heuer, W.D.C. 2007 Reynolds number invariance of the structure inclination angle in wall turbulence. Phys. Rev. Lett. 99 (11), 114504.CrossRefGoogle ScholarPubMed
Matsuda, T. & Sakakibara, J. 2005 On the vortical structure in a round jet. Phys. Fluids 17 (2), 025106.CrossRefGoogle Scholar
Monty, J.P., Stewart, J.A., Williams, R.C. & Chong, M.S. 2007 Large-scale features in turbulent pipe and channel flows. J. Fluid Mech. 589, 147.CrossRefGoogle Scholar
Mullyadzhanov, R.I., Sandberg, R.D., Abdurakipov, S.S., George, W.K. & Hanjalić, K. 2018 Propagating helical waves as a building block of round turbulent jets. Phys. Rev. Fluids 3 (6), 062601.CrossRefGoogle Scholar
Nickels, T.B. & Marusic, I. 2001 On the different contributions of coherentstructures to the spectra of a turbulent round jetand a turbulent boundary layer. J. Fluid Mech. 448, 367–385.CrossRefGoogle Scholar
Nickels, T.B. & Perry, A.E. 1996 An experimental and theoretical study of the turbulent coflowing jet. J. Fluid Mech. 309, 157–182.CrossRefGoogle Scholar
Nogueira, P.A.S., Cavalieri, A.V.G., Jordan, P. & Jaunet, V. 2019 Large-scale streaky structures in turbulent jets. J. Fluid Mech. 873, 211–237.CrossRefGoogle Scholar
Philip, J. & Marusic, I. 2012 Large-scale eddies and their role in entrainment in turbulent jets and wakes. Phys. Fluids 24 (5), 055108.CrossRefGoogle Scholar
Sadeghi, H. & Pollard, A. 2012 Effects of passive control rings positioned in the shear layer and potential core of a turbulent round jet. Phys. Fluids 24 (11), 115103.CrossRefGoogle Scholar
Samie, M., Hutchins, N. & Marusic, I. 2018 Revisiting end conduction effects in constant temperature hot-wire anemometry. Exp. Fluids 59 (9), 133.CrossRefGoogle Scholar
Samie, M., Lavoie, P. & Pollard, A. 2020 A scale-dependent coherence analysis of turbulent round jets including the effects of shear layer manipulation. Intl J. Heat Fluid Flow 82, 108524.CrossRefGoogle Scholar
Schmid, P.J. 2010 Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 656, 5–28.CrossRefGoogle Scholar
Schmidt, O.T., Towne, A., Rigas, G., Colonius, T. & Brès, G.A. 2018 Spectral analysis of jet turbulence. J. Fluid Mech. 855, 953–982.CrossRefGoogle Scholar
Semeraro, O., Bellani, G. & Lundell, F. 2012 Analysis of time-resolved PIV measurements of a confined turbulent jet using POD and Koopman modes. Exp. Fluids 53 (5), 1203–1220.CrossRefGoogle Scholar
Shin, D., Sandberg, R.D. & Richardson, E.S. 2017 Self-similarity of fluid residence time statistics in a turbulent round jet. J. Fluid Mech. 823, 1–25.CrossRefGoogle Scholar
Sillero, J.A., Jiménez, J. & Moser, R.D. 2014 Two-point statistics for turbulent boundary layers and channels at Reynolds numbers up to $\delta ^+ \approx 2000$. Phys. Fluids 26 (10), 105109.CrossRefGoogle Scholar
Suto, H., Matsubara, K., Kobayashi, M., Watanabe, H. & Matsudaira, Y. 2004 Coherent structures in a fully developed stage of a non-isothermal round jet. Heat Transfer Asian Res. 33 (5), 342–356.CrossRefGoogle Scholar
Tomkins, C.D. & Adrian, R.J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.CrossRefGoogle Scholar
Towne, A., Schmidt, O.T. & Colonius, T. 2018 Spectral proper orthogonal decomposition and its relationship to dynamic mode decomposition and resolvent analysis. J. Fluid Mech. 847, 821–867.CrossRefGoogle Scholar
Townsend, A.A.R. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Tso, J. & Hussain, F. 1989 Organized motions in a fully developed turbulent axisymmetric jet. J. Fluid Mech. 203, 425–448.CrossRefGoogle Scholar
Tyliszczak, A. & Geurts, B.J. 2014 Parametric analysis of excited round jets-numerical study. Flow Turbul. Combust. 93 (2), 221–247.CrossRefGoogle Scholar
Ukeiley, L., Tinney, C.E., Mann, R. & Glauser, M. 2007 Spatial correlations in a transonic jet. AIAA J. 45 (6), 1357–1369.CrossRefGoogle Scholar
Wang, Z., He, P., Lv, Y., Zhou, J., Fan, J. & Cen, K. 2010 Direct numerical simulation of subsonic round turbulent jet. Flow Turbul. Combust. 84 (4), 669–686.CrossRefGoogle Scholar
Winant, C.D. & Browand, F.K. 1974 Vortex pairing: the mechanism of turbulent mixing-layer growth at moderate Reynolds number. J. Fluid Mech. 63 (2), 237–255.CrossRefGoogle Scholar
Yoda, M., Hesselink, L. & Mungal, M.G. 1994 Instantaneous three-dimensional concentration measurements in the self-similar region of a round high-Schmidt-number jet. J. Fluid Mech. 279, 313–350.CrossRefGoogle Scholar
Yule, A.J. 1978 Large-scale structure in the mixing layer of a round jet. J. Fluid Mech. 89 (3), 413–432.CrossRefGoogle Scholar
Zaman, K.B.M.Q. & Hussain, A.K.M.F. 1981 Turbulence suppression in free shear flows by controlled excitation. In 13th Fluid and PlasmaDynamics Conference, p. 1338.Google Scholar
Zhou, J., Adrian, R.J., Balachandar, S. & Kendall, T.M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.CrossRefGoogle Scholar