Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-23T10:55:26.560Z Has data issue: false hasContentIssue false
  • English
  • Français

PSI in the case of internal wave beam reflection at a uniform slope

Published online by Cambridge University Press:  21 January 2016

Vamsi K. Chalamalla  and
Sutanu Sarkar
Vamsi K. Chalamalla
Affiliation:
Mechanical and Aerospace Engineering, University of California, San Diego, La Jolla, CA 92093, USA
Sutanu Sarkar*
Affiliation:
Mechanical and Aerospace Engineering, University of California, San Diego, La Jolla, CA 92093, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Two-dimensional numerical simulations are performed to examine internal wave reflection at a sloping boundary. Owing to reflection, the reflected wave amplitude and wavenumber increase. At low values of the incoming wave amplitude, the reflected wave beam is linear and its properties agree well with linear inviscid theory. Linear theory overestimates the reflected wave Froude number, 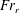$Fr_{r}$, for higher values of incoming wave amplitude. Nonlinearity sets in with increasing value of incoming wave Froude number, 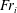$Fr_{i}$, leading to parametric subharmonic instability (PSI) of the reflected wave beam: two subharmonics emerge from the reflection region with frequencies 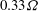$0.33{\it\Omega}$ and 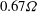$0.67{\it\Omega}$ and wavenumbers that add up to those of the reflected wave. The amplification of Froude number due to reflection must be sufficiently large for PSI to occur implying that the off-criticality in wave angle cannot be too large. The simulations also show that, all other parameters being fixed, a threshold in beam amplitude is required for the onset of PSI in the reflected beam, consistent with results from a previous weakly-nonlinear asymptotic theory for a freely propagating finite-width beam. Growth rates of subharmonic modes at moderate reflected wave amplitude are in reasonable agreement with that theory. However, for $Fr_{r}>0.5$, small scale fluctuations becomes prominent and the subharmonic energy growth rates saturate in the simulations in contrast to the theoretical prediction. Increasing the incoming beam thickness (number of carrier wavelengths) increases the strength of PSI. Keeping the incoming Froude number constant and increasing the incoming Reynolds number by a factor of 50 does not have an effect on the unequal division of frequencies among the subharmonic modes that is found in the simulations.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Internal waves Instability: Parametric instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 789 , 25 February 2016 , pp. 347 - 367
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Benielli, D. & Sommeria, J. 1998 Excitation and breaking of internal gravity waves by parametric instability. J. Fluid Mech. 374, 117–144.Google Scholar
Bourget, B., Dauxois, T., Joubaud, S. & Odier, P. 2013 Experimental study of parametric subharmonic instability for internal plane waves. J. Fluid Mech. 723, 1–20.Google Scholar
Bourget, B., Scolan, H., Dauxois, T., Le Bars, M., Odier, P. & Joubaud, S. 2014 Finite-size effects in parametric subharmonic instability. J. Fluid Mech. 759, 739–750.Google Scholar
Cacchione, D. A., Pratson, L. F. & Ogston, A. S. 2002 The shaping of continental slopes by internal tides. Science 296, 724–727.Google Scholar
Carter, G. S. & Gregg, M. C. 2006 Persistent near-diurnal internal waves observed above a site of m2 barotropic-to-baroclinic conversion. J. Phys. Oceanogr. 36, 1136–1147.Google Scholar
Chalamalla, V. K., Gayen, B., Scotti, A. & Sarkar, S. 2013 Turbulence during the reflection of internal gravity waves at critical and near-critical slopes. J. Fluid Mech. 729, 47–68.Google Scholar
Clark, H. A. & Sutherland, B. R. 2010 Generation, propagation and breaking of an internal wave beam. Phys. Fluids 22, 076601.Google Scholar
Cole, S. T., Rudnick, D. L., Hodges, B. A. & Martin, J. P. 2013 Observations of tidal internal wave beams at Kauai Channel, Hawaii. J. Phys. Oceanogr. 39, 421–436.Google Scholar
Dauxois, T. & Young, W. R. 1999 Near-critical reflection of internal waves. J. Fluid Mech. 390, 271–295.Google Scholar
DeSilva, I. P. D., Imberger, J. & Ivey, G. N. 1997 Localized mixing due to a breaking internal wave ray at a sloping bed. J. Fluid Mech. 350, 1–27.Google Scholar
Gayen, B. & Sarkar, S. 2011 Direct and large-eddy simulations of internal tide generation at a near-critical slope. J. Fluid Mech. 681, 48–79.Google Scholar
Gayen, B. & Sarkar, S. 2013 Degradation of an internal wave beam by parametric subharmonic instability in an upper ocean pycnocline. J. Geophys. Res. 118, 4689–4698.Google Scholar
Gayen, B. & Sarkar, S. 2014 Psi to turbulence during internal wave beam refraction through the upper ocean pycnocline. Geophys. Res. Lett. 41, 8953–8960.Google Scholar
Gerkema, T., Staquet, C. & Bouruet-Aubertot, P. 2006 Decay of semi-diurnal internal-tide beams due to subharmonic resonance. Geophys. Res. Lett. 33, L08604.CrossRefGoogle Scholar
Hasselmann, K. 1967 A criterion for nonlinear wave stability. J. Fluid Mech. 30, 737–739.Google Scholar
Javam, A., Imberger, J. & Armfield, S. W. 1999 Numerical study of internal wave reflection from sloping boundaries. J. Fluid Mech. 396, 183–201.Google Scholar
Javam, A., Imberger, J. & Armfield, S. W. 2000 Numerical study of internal wave-caustic and internal wave-shear interactions in a stratified fluid. J. Fluid Mech. 415, 89–116.Google Scholar
Johnston, T. M. S., Rudnick, D. L., Carter, G. S., Todd, R. E. & Cole, S. T. 2010 Internal tidal beams and mixing near Monterey Bay. J. Geophys. Res. 116, C03017.Google Scholar
Karimi, H. H. & Akylas, T. R. 2014 Parametric subharmonic instability of internal waves: locally confined beams versus monochromatic wavetrains. J. Fluid Mech. 757, 381–402.Google Scholar
Koudella, C. R. & Staquet, C. 2006 Instability mechanisms of a two-dimensional progressive internal gravity wave. J. Fluid Mech. 548, 165–196.Google Scholar
Ledwell, J. R., Montgomery, K. L., Polzin, K. L., Laurent, L. C. St., Schmitt, R. W. & Toole, J. M. 2000 Evidence of enhanced mixing over rough topography in the abyssal ocean. Nature 403, 179–182.Google Scholar
MacKinnon, J. A., Alford, M. H., Sun, O., Pinkel, R., Zhao, Z. & Klymak, J. 2013 Parametric subharmonic instability of the internal tide at 29° N. J. Phys. Oceanogr. 43, 17–28.CrossRefGoogle Scholar
MacKinnon, J. A. & Winters, K. B. 2005 Subtropical catastrophe: significant loss of low-mode tidal energy at 28.9°. Geophys. Res. Lett. 32, L15605.Google Scholar
McEwan, A. D. 1971 Degeneration of resonantly-excited standing internal gravity waves. J. Fluid Mech. 50 (03), 431–448.Google Scholar
Munk, W. & Wunsch, C. 1998 Abyssal recipes II: energetics of tidal and wind mixing. Deep-Sea Res. I 45, 1977–2010.Google Scholar
Polzin, K. L., Toole, J. M., Ledwell, J. R. & Schmitt, R. W. 1997 Spatial variability of turbulent mixing in the abyssal ocean. Science 276, 93–96.Google Scholar
Rodenborn, B. E., Kiefer, D., Zhang, H. P. & Swinney, H. L. 2011 Harmonic generation by reflecting internal waves. Phys. Fluids 23, 026601.Google Scholar
Scotti, A. 2011 Inviscid critical and near-critical reflection of internal waves in the time domain. J. Fluid Mech. 674, 464–488.CrossRefGoogle Scholar
Slinn, D. N. & Riley, J. J. 1998a A model for the simulation of turbulent boundary layers in an incompressible stratified flow. J. Comput. Phys. 34, 550–602.Google Scholar
Slinn, D. N. & Riley, J. J. 1998b Turbulent dynamics of a critically reflecting internal gravity wave. Theor. Comput. Fluid Dyn. 11, 281–303.Google Scholar
Sun, O. & Pinkel, R. 2013 Subharmonic energy transfer from the semidiurnal internal tide to near-diurnal motions over Kaena Ridge, Hawaii. J. Phys. Oceanogr. 43, 766–789.CrossRefGoogle Scholar
Tabaei, A., Akylas, T. R. & Lamb, K. 2005 Nonlinear effects in reflecting and colliding internal wave beams. J. Fluid Mech. 526, 217–243.Google Scholar
Thorpe, S. A. 1968 On standing internal gravity waves of finite amplitude. J. Fluid Mech. 32 (03), 489–528.Google Scholar
Wunsch, C. & Ferrari, R. 2004 Vertical mixing, energy, and the general circulation of the oceans. Annu. Rev. Fluid Mech. 36, 281–314.Google Scholar
Zhou, Q. & Diamessis, P. 2013 Reflection of an internal gravity wave beam off a horizontal free-slip surface. Phys. Fluids 25, 036601.Google Scholar