Published online by Cambridge University Press: 31 March 2015
Gas-phase velocity fluctuations due to mean slip velocity between the gas and solid phases are quantified using particle-resolved direct numerical simulation. These fluctuations are termed pseudo-turbulent because they arise from the interaction of particles with the mean slip even in ‘laminar’ gas–solid flows. The contribution of turbulent and pseudo-turbulent fluctuations to the level of gas-phase velocity fluctuations is quantified in initially ‘laminar’ and turbulent flow past fixed random particle assemblies of monodisperse spheres. The pseudo-turbulent kinetic energy 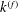 $k^{(f)}$ in steady flow is then characterized as a function of solid volume fraction
$k^{(f)}$ in steady flow is then characterized as a function of solid volume fraction 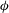 ${\it\phi}$ and the Reynolds number based on the mean slip velocity
${\it\phi}$ and the Reynolds number based on the mean slip velocity 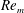 $\mathit{Re}_{m}$. Anisotropy in the Reynolds stress is quantified by decomposing it into isotropic and deviatoric parts, and its dependence on
$\mathit{Re}_{m}$. Anisotropy in the Reynolds stress is quantified by decomposing it into isotropic and deviatoric parts, and its dependence on 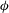 ${\it\phi}$ and
${\it\phi}$ and 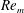 $Re_{m}$ is explained. An algebraic stress model is proposed that captures the dependence of the Reynolds stress on
$Re_{m}$ is explained. An algebraic stress model is proposed that captures the dependence of the Reynolds stress on 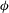 ${\it\phi}$ and
${\it\phi}$ and 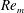 $Re_{m}$. Gas-phase velocity fluctuations in freely evolving suspensions undergoing elastic and inelastic particle collisions are also quantified. The flow corresponds to homogeneous gas–solid systems, with high solid-to-gas density ratio and particle diameter greater than dissipative length scales. It is found that for the parameter values considered here, the level of pseudo-turbulence differs by only 15 % from the values for equivalent fixed beds. The principle of conservation of interphase turbulent kinetic energy transfer is validated by quantifying the interphase transfer terms in the evolution equations of kinetic energy for the gas-phase and solid-phase fluctuating velocity. It is found that the collisional dissipation is negligible compared with the viscous dissipation for the cases considered in this study where the freely evolving suspensions attain a steady state starting from an initial condition where the particles are at rest.
$Re_{m}$. Gas-phase velocity fluctuations in freely evolving suspensions undergoing elastic and inelastic particle collisions are also quantified. The flow corresponds to homogeneous gas–solid systems, with high solid-to-gas density ratio and particle diameter greater than dissipative length scales. It is found that for the parameter values considered here, the level of pseudo-turbulence differs by only 15 % from the values for equivalent fixed beds. The principle of conservation of interphase turbulent kinetic energy transfer is validated by quantifying the interphase transfer terms in the evolution equations of kinetic energy for the gas-phase and solid-phase fluctuating velocity. It is found that the collisional dissipation is negligible compared with the viscous dissipation for the cases considered in this study where the freely evolving suspensions attain a steady state starting from an initial condition where the particles are at rest.
Present address: CD-Adapco, Lebanon, NH 03766, USA.
Present address: National Energy Technology Laboratory, Morgantown, WV 26508, USA.