Published online by Cambridge University Press: 20 March 2020
This paper investigates the properties of the mean momentum balance (MMB) equation in the azimuthal  $\unicode[STIX]{x1D719}$ direction of a turbulent Taylor–Couette flow (TCF). The MMB-
$\unicode[STIX]{x1D719}$ direction of a turbulent Taylor–Couette flow (TCF). The MMB- $\unicode[STIX]{x1D719}$ equation is integrated to determine the properties of the Reynolds shear stress. An approximation is developed for the Reynolds shear stress in the core region of a turbulent TCF, and the dependence of the peak Reynolds shear stress location on the Reynolds number and the gap geometry is revealed. The properties of the global integral of the turbulent Coriolis force are also revealed. For a turbulent TCF with a small gap or at high Reynolds numbers, the global integral of the turbulent Coriolis force is found to be only weakly influenced by the rotation ratio of the cylinders. Two controlling non-dimensional numbers are derived directly from the scaling analysis of the MMB-
$\unicode[STIX]{x1D719}$ equation is integrated to determine the properties of the Reynolds shear stress. An approximation is developed for the Reynolds shear stress in the core region of a turbulent TCF, and the dependence of the peak Reynolds shear stress location on the Reynolds number and the gap geometry is revealed. The properties of the global integral of the turbulent Coriolis force are also revealed. For a turbulent TCF with a small gap or at high Reynolds numbers, the global integral of the turbulent Coriolis force is found to be only weakly influenced by the rotation ratio of the cylinders. Two controlling non-dimensional numbers are derived directly from the scaling analysis of the MMB- $\unicode[STIX]{x1D719}$ equation. The first is a geometry Atwood number
$\unicode[STIX]{x1D719}$ equation. The first is a geometry Atwood number  $A_{t}\stackrel{\text{def}}{=}\unicode[STIX]{x1D6FF}/r_{ctr}$ to characterize the gap geometry, where
$A_{t}\stackrel{\text{def}}{=}\unicode[STIX]{x1D6FF}/r_{ctr}$ to characterize the gap geometry, where  $\unicode[STIX]{x1D6FF}$ is the gap half-width, and
$\unicode[STIX]{x1D6FF}$ is the gap half-width, and  $r_{ctr}$ is the mid-gap radial location. The second is the friction Reynolds number
$r_{ctr}$ is the mid-gap radial location. The second is the friction Reynolds number  $Re_{\unicode[STIX]{x1D70F},i}$ defined as
$Re_{\unicode[STIX]{x1D70F},i}$ defined as  $Re_{\unicode[STIX]{x1D70F},i}\stackrel{\text{def}}{=}\unicode[STIX]{x1D6FF}u_{\unicode[STIX]{x1D70F},i}/\unicode[STIX]{x1D708}$, where
$Re_{\unicode[STIX]{x1D70F},i}\stackrel{\text{def}}{=}\unicode[STIX]{x1D6FF}u_{\unicode[STIX]{x1D70F},i}/\unicode[STIX]{x1D708}$, where  $\unicode[STIX]{x1D708}$ is the kinematic viscosity and
$\unicode[STIX]{x1D708}$ is the kinematic viscosity and  $u_{\unicode[STIX]{x1D70F},i}$ is the friction velocity at the inner cylinder. A new three-layer structure is proposed for the inner half of a turbulent TCF at sufficiently high Reynolds number, based on the force balance in the MMB-
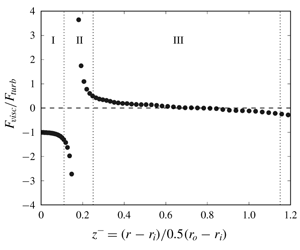
$u_{\unicode[STIX]{x1D70F},i}$ is the friction velocity at the inner cylinder. A new three-layer structure is proposed for the inner half of a turbulent TCF at sufficiently high Reynolds number, based on the force balance in the MMB- $\unicode[STIX]{x1D719}$ equation. Layer I is an inner layer, where the force balance is between the viscous force and the Reynolds shear force:
$\unicode[STIX]{x1D719}$ equation. Layer I is an inner layer, where the force balance is between the viscous force and the Reynolds shear force:  $F_{visc}\approx -F_{turb}$. Layer III occupies the core of the gap, where the force balance is between the turbulent Coriolis force and the Reynolds shear force:
$F_{visc}\approx -F_{turb}$. Layer III occupies the core of the gap, where the force balance is between the turbulent Coriolis force and the Reynolds shear force:  $F_{cori}\approx -F_{turb}$. In Layer II, all three forces contribute to the balance. An inner scaling is developed for Layer I, and an outer scaling is developed for Layer III. The inner and outer scalings are verified against direct numerical simulation data. Similarities and differences between the turbulent TCF and a pressure-driven turbulent channel flow are elucidated.
$F_{cori}\approx -F_{turb}$. In Layer II, all three forces contribute to the balance. An inner scaling is developed for Layer I, and an outer scaling is developed for Layer III. The inner and outer scalings are verified against direct numerical simulation data. Similarities and differences between the turbulent TCF and a pressure-driven turbulent channel flow are elucidated.