Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-26T08:29:08.153Z Has data issue: false hasContentIssue false
  • English
  • Français

Propagation of viscous currents on a porous substrate with finite capillary entry pressure

Published online by Cambridge University Press:  19 July 2016

Roiy Sayag  and
Jerome A. Neufeld
Roiy Sayag*
Affiliation:
Department of Environmental Physics, Blaustein Institutes for Desert Research, Ben-Gurion University of the Negev, Sede Boqer Campus, 8499000, Israel Department of Mechanical Engineering, Ben-Gurion University of the Negev, Beer-Sheva 8410501, Israel
Jerome A. Neufeld
Affiliation:
BP Institute, University of Cambridge, Cambridge CB3 0EZ, UK Department of Earth Sciences, Bullard laboratories, University of Cambridge, Cambridge CB3 0EZ, UK Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Cambridge CB3 0WA, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the propagation of viscous gravity currents over a thin porous substrate with finite capillary entry pressure. Near the origin, where the current is deep, propagation of the current coincides with leakage through the substrate. Near the nose of the current, where the current is thin and the fluid pressure is below the capillary entry pressure, drainage is absent. Consequently the flow can be characterised by the evolution of drainage and fluid fronts. We analyse this flow using numerical and analytical techniques combined with laboratory-scale experiments. At early times, we find that the position of both fronts evolve as 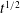$t^{1/2}$, similar to an axisymmetric gravity current on an impermeable substrate. At later times, the growing effect of drainage inhibits spreading, causing the drainage front to logarithmically approach a steady position. In contrast, the asymptotic propagation of the fluid front is quasi-self-similar, having identical structure to the solution of gravity currents on an impermeable substrate, only with slowly varying fluid flux. We benchmark these theoretical results with laboratory experiments that are consistent with our modelling assumption, but that also highlight the detailed dynamics of drainage inhibited by finite capillary pressure.

JFM classification

Geophysical and Geological Flows: Gravity currents Interfacial Flows (free surface): Interfacial Flows (free surface) Low-Reynolds-number flows: Porous media
Type
Papers
Information
Journal of Fluid Mechanics , Volume 801 , 25 August 2016 , pp. 65 - 90
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acton, J. M., Huppert, H. E. & Worster, M. G. 2001 Two-dimensional viscous gravity currents flowing over a deep porous medium. J. Fluid Mech. 440, 359–380.Google Scholar
Bear, J. 1988 Dynamics of Fluids in Porous Media. Dover Civil and Mechanical Engineering.Google Scholar
Boczar-Karakiewicz, B., Bona, J. L. & Pelchat, B. 1991 Interaction of internal waves with the seabed on continental shelves. Cont. Shelf Res. 11, 1181–1197.Google Scholar
Boulange-Petermann, L., Gabet, C. & Baroux, B. 2006 Relation between the cleanability of bare or polysiloxane-coated stainless steels and their water contact angle hysteresis. J. Adhes. Sci. Technol. 20 (13), 1463–1474.Google Scholar
Das, S. B., Joughin, I., Behn, M. D., Howat, I. M., King, M. A., Lizarralde, D. & Bhatia, M. P. 2008 Fracture propagation to the base of the greenland ice sheet during supraglacial lake drainage. Science 320 (5877), 778–781.Google Scholar
Davis, S. H. & Hocking, L. M. 1999 Spreading and imbibition of viscous liquid on a porous base. Phys. Fluids 11 (1), 48–57.Google Scholar
Davis, S. H. & Hocking, L. M. 2000 Spreading and imbibition of viscous liquid on a porous base II. Phys. Fluids 12 (7), 1646–1655.Google Scholar
Grobelbauer, H. P., Fannelop, T. K. & Britter, R. E. 1993 The propagation of intrusion fronts of high-density ratios. J. Fluid Mech. 250, 669–687.Google Scholar
Huppert, H. E. 1982 The propagation of two-dimensional and axisymmetric viscous gravity currents over a rigid horizontal surface. J. Fluid Mech. 121, 43–58.Google Scholar
Huppert, H. E. 2006 Gravity currents: a personal perspective. J. Fluid Mech. 554, 299–322.Google Scholar
Huppert, H. E. & Neufeld, J. A. 2014 The fluid mechanics of carbon dioxide sequestration. Annu. Rev. Fluid Mech. 46 (1), 255–272.Google Scholar
Huppert, H. E. & Woods, A. W. 1995 Gravity-driven flows in porous layers. J. Fluid Mech. 292, 55–69.Google Scholar
Llewellin, E. W., Mader, H. M. & Wilson, S. D. R. 2002 The rheology of a bubbly liquid. Proc. R. Soc. Lond. A 458 (2020), 987–1016.Google Scholar
Marino, B. M. & Thomas, L. P. 2002 Spreading of a gravity current over a permeable surface. J. Hydraul. Engng 128 (5), 527–533.Google Scholar
Pirat, C., Mathis, C., Maïssa, P. & Gil, L. 2004 Structures of a continuously fed two-dimensional viscous film under a destabilizing gravitational force. Phys. Rev. Lett. 92 (10), 104501.Google Scholar
Pritchard, D., Woods, A. W. & Hogg, A. J. 2001 On the slow draining of a gravity current moving through a layered permeable medium. J. Fluid Mech. 444 (0), 23–47.Google Scholar
Simpson, J. E. 1999 Gravity Currents: In the Environment and the Laboratory. Cambridge University Press.Google Scholar
Spannuth, M. J., Neufeld, J. A., Wettlaufer, J. S. & Worster, M. G. 2009 Axisymmetric viscous gravity currents flowing over a porous medium. J. Fluid Mech. 622, 135–144.Google Scholar
Tadmor, R. 2004 Line energy and the relation between advancing, receding, and young contact angles. Langmuir 20 (18), 7659–7664.Google Scholar
Thomas, L. P., Marino, B. M. & Linden, P. F. 1998 Gravity currents over porous substrates. J. Fluid Mech. 366 (0), 239–258.Google Scholar
Thomas, L. P., Marino, B. M. & Linden, P. F. 2004 Lock-release inertial gravity currents over a thick porous layer. J. Fluid Mech. 503, 299–319.Google Scholar
Ungarish, M. & Huppert, H. E. 2000 High-Reynolds-number gravity currents over a porous boundary: shallow-water solutions and box-model approximations. J. Fluid Mech. 418 (0), 1–23.Google Scholar
Woods, A. W. & Farcas, A. 2009 Capillary entry pressure and the leakage of gravity currents through a sloping layered permeable rock. J. Fluid Mech. 618, 361–379.Google Scholar

Sayag and Neufeld supplementary movie

Videos of laboratory experiment of a viscous current propagating on a perforated surface, at the presence of finite capillary entry pressure, showing a side view of the evolving current that captures the surface current that propagates over the substrate and the detailed dynamics of the drainage inhibited by capillary pressure.

Download Sayag and Neufeld supplementary movie(Video)
Video 5.2 MB

Sayag and Neufeld supplementary movie

A simultaneous oblique view of the surface current shown in Movie 1.

Download Sayag and Neufeld supplementary movie(Video)
Video 20.9 MB