Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-01-08T10:36:17.918Z Has data issue: false hasContentIssue false
  • English
  • Français

The propagation of gravity currents in a V-shaped triangular cross-section channel: experiments and theory

Published online by Cambridge University Press:  31 July 2014

Marius Ungarish ,
Catherine A. Mériaux  and
Cathy B. Kurz-Besson
Marius Ungarish*
Affiliation:
Department of Computer Science, Technion, Israel Institute of Technology, Haifa 32000, Israel
Catherine A. Mériaux
Affiliation:
Instituto Dom Luiz, Faculdade de Ciências, Universidade de Lisboa, Campo Grande 1749-016 Lisboa, Portugal
Cathy B. Kurz-Besson
Affiliation:
Instituto Dom Luiz, Faculdade de Ciências, Universidade de Lisboa, Campo Grande 1749-016 Lisboa, Portugal
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the motion of high-Reynolds-number gravity currents (GCs) in a horizontal channel of V-shaped cross-section combining lock-exchange experiments and a theoretical model. While all previously published experiments in V-shaped channels were performed with the special configuration of the full-depth lock, we present the first part-depth experiment results. 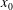A fixed volume of saline, that was initially of length $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}x_0$ and height 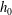$h_0$ in a lock and embedded in water of height $H_0$ in a long tank, was released from rest and the propagation was recorded over a distance of typically 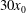$ 30 x_0$. In all of the tested cases the current displays a slumping stage of constant speed 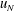$u_N$ over a significant distance 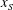$x_S$, followed by a self-similar stage up to the distance 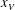$x_V$, where transition to the viscous regime occurs. The new data and insights of this study elucidate the influence of the height ratio 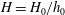$H = H_0/h_0$ and of the initial Reynolds number 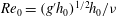${\mathit{Re}}_0 = (g^{\prime }h_0)^{{{1/2}}} h_0/ \nu $, on the motion of the triangular GC; 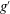$g^{\prime }$ and $\nu $ are the reduced gravity and kinematic viscosity coefficient, respectively. We demonstrate that the speed of propagation 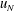$u_N$ scaled with 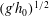$(g^{\prime } h_0)^{{{1/2}}}$ increases with 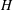$H$, while 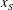$x_S$ decreases with $H$, and 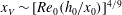$x_V \sim [{\mathit{Re}}_0(h_0/x_0)]^{{4/9}}$. The initial propagation in the triangle is 50 % more rapid than in a standard flat-bottom channel under similar conditions. Comparisons with theoretical predictions show good qualitative agreements and fair quantitative agreement; the major discrepancy is an overpredicted 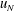$u_N$, similar to that observed in the standard flat bottom case.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Gravity currents
Type
Papers
Information
Journal of Fluid Mechanics , Volume 754 , 10 September 2014 , pp. 232 - 249
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bastina, S., Drobinskia, P., Dabasb, A., Delvillec, P., Reitebuchd, O. & Werner, C. 2005 Impact of the Rhone and Durance valleys on sea-breeze circulation in the Marseille area. Atmos. Res. 74, 303–328.CrossRefGoogle Scholar
Benjamin, T. B. 1968 Gravity currents and related phenomena. J. Fluid Mech. 31, 209–248.CrossRefGoogle Scholar
Birman, V. K., Martin, J. E. & Meiburg, E. 2005 The non-Boussinesq lock exchange problem. Part 2: high-resolution simulations. J. Fluid Mech. 537, 125–144.Google Scholar
Bonnecaze, R. T., Huppert, H. E. & Lister, J. R. 1993 Particle-driven gravity currents. J. Fluid Mech. 250, 339–369.CrossRefGoogle Scholar
Bonometti, T., Balachandar, S. & Magnaudet, J. 2008 Wall effects in non-Boussinesq density currents. J. Fluid Mech. 616, 445–475.CrossRefGoogle Scholar
Bonometti, T., Ungarish, M. & Balachandar, S. 2011 A numerical investigation of constant-volume non-Boussinesq gravity currents in deep ambient. J. Fluid Mech. 673, 574–602.CrossRefGoogle Scholar
Constantinescu, G. 2014 Les of lock-exchange compositional gravity currents: a brief review of some recent results. Environ. Fluid Mech. 14, 295–317.CrossRefGoogle Scholar
Gohm, A., Mayr, G. J., Darby, L. S. & Banta, R. M. 2010 Evolution and structure of a cold front in an Alpine valley as revealed by a Doppler lidar. Q. J. R. Meteorol. Soc. 136, 962–977.CrossRefGoogle Scholar
Hallworth, M., Huppert, H. E., Phillips, J. & Sparks, R. 1996 Entrainment into two-dimensional and axisymmetric turbulent gravity currents. J. Fluid Mech. 308, 289–311.CrossRefGoogle Scholar
Hiscott, R. N., Aksu, A. E., Flood, R. D., Kostylev, V. & Yasar, D. 2013 Widespread overspill from a saline density-current channel and its interaction with topography on the south–west Black Sea shelf. Sedimentology 60, 1639–1667.CrossRefGoogle Scholar
Hogg, A., Ungarish, M. & Huppert, H. E. 2000 Particle-driven gravity currents: asymptotic and box-model solutions. Eur. J. Mech. (B/Fluids) 19, 139–165.CrossRefGoogle Scholar
Huppert, H. E. & Simpson, J. E. 1980 The slumping of gravity currents. J. Fluid Mech. 99, 785–799.CrossRefGoogle Scholar
Johnson, C. G. & Hogg, A. J. 2013 Entraining gravity currents. J. Fluid Mech. 731, 477–508.CrossRefGoogle Scholar
Kneller, B. & Buckee, C. 2000 The structure and fluid mechanics of turbidity currents: a review of some recent studies and their geological implications. Sedimentology 47, 62–94.CrossRefGoogle Scholar
Lowe, R. J., Rottman, J. W. & Linden, P. F. 2005 The non-Boussinesq lock exchange problem. Part 1: theory and experiments. J. Fluid Mech. 537, 101–124.Google Scholar
Marino, B. M. & Thomas, L. P. 2009 Front condition for gravity currents in channels of nonrectangular symmetric cross-section shapes. Trans. ASME J. Fluids Engng 131 (5), 051201.CrossRefGoogle Scholar
Marino, B. M. & Thomas, L. P. 2011 Dam-break release of a gravity current in a power-law channel section. J. Phys.: Conf. Ser. 296, 012008.Google Scholar
Mériaux, C. A. & Kurz-Besson, C. B. 2012 Sedimentation from binary suspensions in a turbulent gravity current along a V-shaped valley. J. Fluid Mech. 712, 624–645.CrossRefGoogle Scholar
Monaghan, J., Mériaux, C., Huppert, H. & Mansour, J. 2009a Particulate gravity currents along V-shaped valleys. J. Fluid Mech. 631, 419–440.CrossRefGoogle Scholar
Monaghan, J., Mériaux, C., Huppert, H. & Monaghan, J. 2009b High Reynolds number gravity currents along V-shaped valleys. Eur. J. Mech. (B/Fluids) 28 (5), 651–659.Google Scholar
Nasr-Azadani, M. M. & Meiburg, E. 2014 Turbidity currents interacting with three-dimensional seaflor topography. J. Fluid Mech. 745, 409–443.CrossRefGoogle Scholar
Rottman, J. & Simpson, J. 1983 Gravity currents produced by instantaneous release of a heavy fluid in a rectangular channel. J. Fluid Mech. 135, 95–110.CrossRefGoogle Scholar
Rotunno, R., Klemp, J. B., Bryan, G. H. & Muraki, D. J. 2011 Models of non-Boussinesq lock-exchange flow. J. Fluid Mech. 675, 1–26.CrossRefGoogle Scholar
Shin, J. O., Dalziel, S. B. & Linden, P. F. 2004 Gravity currents produced by lock exchange. J. Fluid Mech. 521, 1–34.Google Scholar
Simpson, J. E. 1997 Gravity Currents in the Environment and the Laboratory. Cambridge University Press.Google Scholar
Takagi, D. & Huppert, H. E. 2007 The effect of confining boundaries on viscous gravity currents. J. Fluid Mech. 577, 495–505.Google Scholar
Ungarish, M. 2009 An Introduction to Gravity Currents and Intrusions. Chapman & Hall/CRC Press.CrossRefGoogle Scholar
Ungarish, M. 2012 A general solution of Benjamin-type gravity current in a channel of non-rectangular cross-section. Environ. Fluid Mech. 12 (3), 251–263.CrossRefGoogle Scholar
Ungarish, M. 2013 Two-layer shallow-water dam-break solutions for gravity currents in non-rectangular cross-area channels. J. Fluid Mech. 732, 537–570.Google Scholar
Zemach, T. & Ungarish, M. 2013 Gravity currents in non-rectangular cross-section channels: analytical and numerical solutions of the one-layer shallow-water model for high-Reynolds-number propagation. Phys. Fluids 25, 026601.CrossRefGoogle Scholar

Ungarish supplementary movie

The propagation of the current, top view.

Download Ungarish supplementary movie(Video)
Video 15.9 MB