Hostname: page-component-669899f699-b58lm Total loading time: 0 Render date: 2025-04-25T20:48:32.613Z Has data issue: false hasContentIssue false
  • English
  • Français

Prolate spheroids settling in a quiescent fluid: clustering, microstructures and collisions

Published online by Cambridge University Press:  04 December 2024

Xinyu Jiang Open the ORCID record for Xinyu Jiang [Opens in a new window] ,
Chunxiao Xu Open the ORCID record for Chunxiao Xu [Opens in a new window]  and
Lihao Zhao Open the ORCID record for Lihao Zhao [Opens in a new window]
Xinyu Jiang
Affiliation:
AML, Department of Engineering Mechanics, Tsinghua University, Beijing 100084, PR China
Chunxiao Xu
Affiliation:
AML, Department of Engineering Mechanics, Tsinghua University, Beijing 100084, PR China
Lihao Zhao*
Affiliation:
AML, Department of Engineering Mechanics, Tsinghua University, Beijing 100084, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

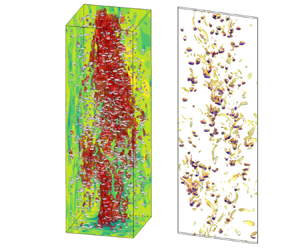
In this study we investigate the sedimentation of prolate spheroids in a quiescent fluid by means of the particle-resolved direct numerical simulation. With the increase of the particle volume fraction $\phi$ from $0.1\,\%$ to $10\,\%$, we observe a non-monotonic variation of the mean settling velocity of particles, $\langle V_s \rangle$. By virtue of the Voronoi analysis, we find that the degree of particle clustering is highest when $\langle V_s \rangle$ reaches the local maximum at $\phi =1\,\%$. Under the swarm effect, clustered particles are found to preferentially sample downward fluid flows in the wake regions, leading to the enhancement of the settling speed. As for lower or higher volume fractions, the tendency of particle clustering and the preferential sampling of downward flows are attenuated. The hindrance effect becomes predominant when the volume fraction exceeds 5 % and reduces $\langle V_s \rangle$ to less than the isolated settling velocity. Particle orientation plays a minor role in the mean settling velocity, although individual prolate particles still tend to settle faster in suspensions when they deviate more from the broad-side-on alignment. Moreover, we also demonstrate that particles are prone to form column-like microstructures in dilute suspensions under the effect of wake-induced hydrodynamic attractions. The radial distribution function is higher at a lower volume fraction. As a result, the collision rate scaled by the particle number density decreases with the increasing volume fraction. By contrast, as another contribution to the particle collision rate, the relative radial velocity for nearby particles shows a minor degree of variation due to the lubrication effect.

JFM classification

Multiphase and Particle-laden Flows: Particle/fluid flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1000 , 10 December 2024 , A49
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Anoukou, K., Brenner, R., Hong, F., Pellerin, M. & Danas, K. 2018 Random distribution of polydisperse ellipsoidal inclusions and homogenization estimates for porous elastic materials. Comput. Struct. 210, 87–101.CrossRefGoogle Scholar
Ardekani, M.N., Costa, P., Breugem, W.P. & Brandt, L. 2016 Numerical study of the sedimentation of spheroidal particles. Intl J. Multiphase Flow 87, 16–34.CrossRefGoogle Scholar
Arguedas-Leiva, J., Słomka, J., Lalescu, C.C., Stocker, R. & Wilczek, M. 2022 Elongation enhances encounter rates between phytoplankton in turbulence. Proc. Natl Acad. Sci. USA 119 (32), e2203191119.CrossRefGoogle ScholarPubMed
Ayala, O., Rosa, B. & Wang, L.-P. 2008 Effects of turbulence on the geometric collision rate of sedimenting droplets. Part 2. Theory and parameterization. New J. Phys. 10 (7), 075016.CrossRefGoogle Scholar
Breugem, W.-P. 2012 A second-order accurate immersed boundary method for fully resolved simulations of particle-laden flows. J. Comput. Phys. 231 (13), 4469–4498.CrossRefGoogle Scholar
Chen, S., Chen, X., Wan, D., Sun, X., Ji, L., Wu, K., Yang, F. & Wang, G. 2020 Particle-resolved direct numerical simulation of collisions of bidisperse inertial particles in a homogeneous isotropic turbulence. Powder Technol. 376, 72–79.CrossRefGoogle Scholar
Chen, S.-H., Ku, Y. & Lin, C.-A. 2019 Simulations of settling object using moving domain and immersed-boundary method. Comput. Fluids 179, 735–743.CrossRefGoogle Scholar
Chouippe, A., Kidanemariam, A.G., Derksen, J., Wachs, A. & Uhlmann, M. 2023 6 – results from particle-resolved simulations. In Modeling Approaches and Computational Methods for Particle-Laden Turbulent Flows (ed. S. Subramaniam & S. Balachandar), pp. 185–216. Academic Press.CrossRefGoogle Scholar
Chrust, M., Bouchet, G. & Dušek, J. 2013 Numerical simulation of the dynamics of freely falling discs. Phys. Fluids 25 (4), 044102.CrossRefGoogle Scholar
Climent, E. & Maxey, M.R. 2003 Numerical simulations of random suspensions at finite Reynolds numbers. Intl J. Multiphase Flow 29 (4), 579–601.CrossRefGoogle Scholar
Costa, P., Boersma, B.J., Westerweel, J. & Breugem, W.-P. 2015 Collision model for fully resolved simulations of flows laden with finite-size particles. Phys. Rev. E 92 (5), 053012.CrossRefGoogle ScholarPubMed
Dabade, V., Marath, N.K. & Subramanian, G. 2016 The effect of inertia on the orientation dynamics of anisotropic particles in simple shear flow. J. Fluid Mech. 791, 631–703.CrossRefGoogle Scholar
Di Felice, R. 1999 The sedimentation velocity of dilute suspensions of nearly monosized spheres. Intl J. Multiphase Flow 25 (4), 559–574.CrossRefGoogle Scholar
Doychev, T. 2014 The dynamics of finite-size settling particles. PhD thesis, Karlsruhe Institute of Technology.Google Scholar
Ern, P., Risso, F., Fabre, D. & Magnaudet, J. 2012 Wake-induced oscillatory paths of bodies freely rising or falling in fluids. Annu. Rev. Fluid Mech. 44 (1), 97–121.CrossRefGoogle Scholar
Eshghinejadfard, A., Abdelsamie, A., Janiga, G. & Thévenin, D. 2016 Direct-forcing immersed boundary lattice Boltzmann simulation of particle/fluid interactions for spherical and non-spherical particles. Particuology 25, 93–103.CrossRefGoogle Scholar
Ferenc, J. & Néda, Z. 2007 On the size distribution of Poisson Voronoi cells. Physica A 385 (2), 518–526.CrossRefGoogle Scholar
Fornari, W., Ardekani, M.N. & Brandt, L. 2018 Clustering and increased settling speed of oblate particles at finite Reynolds number. J. Fluid Mech. 848, 696–721.CrossRefGoogle Scholar
Fornari, W., Picano, F. & Brandt, L. 2016 Sedimentation of finite-size spheres in quiescent and turbulent environments. J. Fluid Mech. 788, 640–669.CrossRefGoogle Scholar
Fornari, W., Zade, S., Brandt, L. & Picano, F. 2019 Settling of finite-size particles in turbulence at different volume fractions. Acta Mech. 230 (2), 413–430.CrossRefGoogle Scholar
Fortes, A.F., Joseph, D.D. & Lundgren, T.S. 1987 Nonlinear mechanics of fluidization of beds of spherical particles. J. Fluid Mech. 177, 467–483.CrossRefGoogle Scholar
Garside, J. & Al-Dibouni, M.R. 1977 Velocity-voidage relationships for fluidization and sedimentation in solid-liquid systems. Ind. Engng Chem. Process. Des. Dev. 16 (2), 206–214.CrossRefGoogle Scholar
Glowinski, R., Pan, T.W., Hesla, T.I., Joseph, D.D. & Périaux, J. 2001 A fictitious domain approach to the direct numerical simulation of incompressible viscous flow past moving rigid bodies: application to particulate flow. J. Comput. Phys. 169 (2), 363–426.CrossRefGoogle Scholar
Grabowski, W.W. & Wang, L.-P. 2013 Growth of cloud droplets in a turbulent environment. Annu. Rev. Fluid Mech. 45 (1), 293–324.CrossRefGoogle Scholar
Grujić, A., Bhatnagar, A., Sardina, G. & Brandt, L. 2024 Collisions among elongated settling particles: the twofold role of turbulence. Phys. Fluids 36 (1), 013319.CrossRefGoogle Scholar
Guazzelli, É. & Hinch, J. 2011 Fluctuations and instability in sedimentation. Annu. Rev. Fluid Mech. 43 (1), 97–116.CrossRefGoogle Scholar
Happel, J. & Brenner, H. 1983 Low Reynolds Number Hydrodynamics. D. Reidel Publishing Co.CrossRefGoogle Scholar
Horowitz, M. & Williamson, C.H.K. 2010 The effect of Reynolds number on the dynamics and wakes of freely rising and falling spheres. J. Fluid Mech. 651, 251–294.CrossRefGoogle Scholar
Huang, H., Yang, X. & Lu, X.-Y. 2014 Sedimentation of an ellipsoidal particle in narrow tubes. Phys. Fluids 26 (5), 053302.CrossRefGoogle Scholar
Huisman, S.G., Barois, T., Bourgoin, M., Chouippe, A., Doychev, T., Huck, P., Morales, C.E.B., Uhlmann, M. & Volk, R. 2016 Columnar structure formation of a dilute suspension of settling spherical particles in a quiescent fluid. Phys. Rev. Fluids 1 (7), 074204.CrossRefGoogle Scholar
Iaccarino, G. & Mittal, R. 2004 Immersed boundary method. Annu. Rev. Fluid Mech. 37 (37), 239–261.Google Scholar
Jenny, M., Duek, J. & Bouchet, G. 2004 Instabilities and transition of a sphere falling or ascending freely in a Newtonian fluid. J. Fluid Mech. 508, 201–239.CrossRefGoogle Scholar
Jiang, X., Huang, W., Xu, C. & Zhao, L. 2024 A flow-reconstruction based approach for the computation of hydrodynamic stresses on immersed body surface. J. Comput. Phys. 508, 113025.CrossRefGoogle Scholar
Jucha, J., Naso, A., Lévêque, E. & Pumir, A. 2018 Settling and collision between small ice crystals in turbulent flows. Phys. Rev. Fluids 3 (1), 014604.CrossRefGoogle Scholar
Kajishima, T. 2004 Influence of particle rotation on the interaction between particle clusters and particle-induced turbulence. Intl J. Heat Fluid Flow 25 (5), 721–728.CrossRefGoogle Scholar
Kajishima, T. & Takiguchi, S. 2002 Interaction between particle clusters and particle-induced turbulence. Intl J. Heat Fluid Flow 23 (5), 639–646.CrossRefGoogle Scholar
Khayat, R.E. & Cox, R.G. 1989 Inertia effects on the motion of long slender bodies. J. Fluid Mech. 209, 435–462.CrossRefGoogle Scholar
Kidanemariam, A.G., Chan-Braun, C., Doychev, T. & Uhlmann, M. 2013 Direct numerical simulation of horizontal open channel flow with finite-size, heavy particles at low solid volume fraction. New J. Phys. 15 (2), 025031.CrossRefGoogle Scholar
Kim, K., Baek, S.-J. & Sung, H.J. 2002 An implicit velocity decoupling procedure for the incompressible Navier–Stokes equations. Intl J. Numer. Meth. Fluids 38 (2), 125–138.CrossRefGoogle Scholar
Koch, D.L. & Hill, R.J. 2001 Inertial effects in suspension and porous-media flows. Annu. Rev. Fluid Mech. 33 (1), 619–647.CrossRefGoogle Scholar
Kuusela, E., Lahtinen, J.M. & Ala-Nissila, T. 2003 Collective effects in settling of spheroids under steady-state sedimentation. Phys. Rev. Lett. 90 (9), 094502.CrossRefGoogle ScholarPubMed
Lu, J., Xu, X., Zhong, S., Ni, R. & Tryggvason, G. 2023 The dynamics of suspensions of prolate spheroidal particles—effects of volume fraction. Intl J. Multiphase Flow 165, 104469.CrossRefGoogle Scholar
Mallios, S.A., Drakaki, E. & Amiridis, V. 2020 Effects of dust particle sphericity and orientation on their gravitational settling in the Earth's atmosphere. J. Aerosol Sci. 150, 105634.CrossRefGoogle Scholar
Monchaux, R., Bourgoin, M. & Cartellier, A. 2010 Preferential concentration of heavy particles: a Voronoï analysis. Phys. Fluids 22 (10), 103304.CrossRefGoogle Scholar
Moriche, M., Hettmann, D., García-Villalba, M. & Uhlmann, M. 2023 On the clustering of low-aspect-ratio oblate spheroids settling in ambient fluid. J. Fluid Mech. 963, A1.CrossRefGoogle Scholar
Moriche, M., Uhlmann, M. & Dušek, J. 2021 A single oblate spheroid settling in unbounded ambient fluid: a benchmark for simulations in steady and unsteady wake regimes. Intl J. Multiphase Flow 136, 103519.CrossRefGoogle Scholar
Peskin, C.S. 2002 The immersed boundary method. Acta Numer. 11, 479–517.CrossRefGoogle Scholar
Pruppacher, H.R. & Klett, J.D. 2010 Microphysics of Clouds and Precipitation, chap. 11.6. Springer.CrossRefGoogle Scholar
Pumir, A. & Wilkinson, M. 2016 Collisional aggregation due to turbulence. Annu. Rev. Condens. Matter Phys. 7 (1), 141–170.CrossRefGoogle Scholar
Raaghav, S.K.R., Poelma, C. & Breugem, W.-P. 2022 Path instabilities of a freely rising or falling sphere. Intl J. Multiphase Flow 153, 104111.CrossRefGoogle Scholar
Rahmani, M. & Wachs, A. 2014 Free falling and rising of spherical and angular particles. Phys. Fluids 26, 083301.CrossRefGoogle Scholar
Richardson, J.F. & Zaki, W.N. 1954 The sedimentation of a suspension of uniform spheres under conditions of viscous flow. Chem. Engng Sci. 3 (2), 65–73.CrossRefGoogle Scholar
Risso, F. 2018 Agitation, mixing, and transfers induced by bubbles. Annu. Rev. Fluid Mech. 50 (1), 25–48.CrossRefGoogle Scholar
Roma, A.M., Peskin, C.S. & Berger, M.J. 1999 An adaptive version of the immersed boundary method. J. Comput. Phys. 153 (2), 509–534.CrossRefGoogle Scholar
Saffman, P.G. & Turner, J.S. 1956 On the collision of drops in turbulent clouds. J. Fluid Mech. 1, 16–30.CrossRefGoogle Scholar
Saintillan, D., Shaqfeh, E.S.G. & Darve, E. 2006 The growth of concentration fluctuations in dilute dispersions of orientable and deformable particles under sedimentation. J. Fluid Mech. 553, 347–388.CrossRefGoogle Scholar
Seyed-Ahmadi, A. & Wachs, A. 2019 Dynamics and wakes of freely settling and rising cubes. Phys. Rev. Fluids 4 (7), 074304.CrossRefGoogle Scholar
Seyed-Ahmadi, A. & Wachs, A. 2021 Sedimentation of inertial monodisperse suspensions of cubes and spheres. Phys. Rev. Fluids 6 (4), 044306.CrossRefGoogle Scholar
Shaw, R.A. 2003 Particle-turbulence interactions in atmospheric clouds. Annu. Rev. Fluid Mech. 35 (1), 183–227.CrossRefGoogle Scholar
Shin, M., Koch, D.L. & Subramanian, G. 2009 Structure and dynamics of dilute suspensions of finite-Reynolds-number settling fibers. Phys. Fluids 21 (12), 123304.CrossRefGoogle Scholar
Siewert, C., Kunnen, R.P.J. & Schröder, W. 2014 Collision rates of small ellipsoids settling in turbulence. J. Fluid Mech. 758, 686–701.CrossRefGoogle Scholar
Slomka, J. & Stocker, R. 2020 On the collision of rods in a quiescent fluid. Proc. Natl Acad. Sci. 117 (7), 3372–3374.CrossRefGoogle Scholar
Sundaram, S. & Collins, L.R. 1997 Collision statistics in an isotropic particle-laden turbulent suspension. Part 1. Direct numerical simulations. J. Fluid Mech. 335, 75–109.CrossRefGoogle Scholar
Tagawa, Y., Roghair, I., Prakash, V.N., Van Sint Annaland, M., Kuipers, H., Sun, C. & Lohse, D. 2013 The clustering morphology of freely rising deformable bubbles. J. Fluid Mech. 721, R2.CrossRefGoogle Scholar
Tavanashad, V., Passalacqua, A. & Subramaniam, S. 2021 Particle-resolved simulation of freely evolving particle suspensions: flow physics and modeling. Intl J. Multiphase Flow 135, 103533.CrossRefGoogle Scholar
Ten Cate, A., Nieuwstad, C.H., Derksen, J.J. & Van den Akker, H.E.A. 2002 Particle imaging velocimetry experiments and lattice–Boltzmann simulations on a single sphere settling under gravity. Phys. Fluids 14 (11), 4012–4025.CrossRefGoogle Scholar
Tenneti, S., Garg, R. & Subramaniam, S. 2011 Drag law for monodisperse gas–solid systems using particle-resolved direct numerical simulation of flow past fixed assemblies of spheres. Intl J. Multiphase Flow 37, 1072–1092.CrossRefGoogle Scholar
Trudnowska, E., Lacour, L., Ardyna, M., Rogge, A., Irisson, J.O., Waite, A.M., Babin, M. & Stemmann, L. 2021 Marine snow morphology illuminates the evolution of phytoplankton blooms and determines their subsequent vertical export. Nat. Commun. 12 (1), 2816.CrossRefGoogle ScholarPubMed
Uhlmann, M. 2005 An immersed boundary method with direct forcing for the simulation of particulate flows. J. Comput. Phys. 209 (2), 448–476.CrossRefGoogle Scholar
Uhlmann, M. 2020 Voronoï tessellation analysis of sets of randomly placed finite-size spheres. Physica A 555, 124618.CrossRefGoogle Scholar
Uhlmann, M. & Doychev, T. 2014 Sedimentation of a dilute suspension of rigid spheres at intermediate Galileo numbers: the effect of clustering upon the particle motion. J. Fluid Mech. 752, 310–348.CrossRefGoogle Scholar
Voth, G.A. & Soldati, A. 2017 Anisotropic particles in turbulence. Annu. Rev. Fluid Mech. 49 (1), 249–276.CrossRefGoogle Scholar
Wang, H., Zhang, B., Li, X., Xiao, Y. & Yang, C. 2022 Modeling total drag force exerted on particles in dense swarm from experimental measurements using an inline image-based method. Chem. Engng J. 431, 133485.CrossRefGoogle Scholar
Wang, L.-P., Ayala, O., Kasprzak, S.E. & Grabowski, W.W. 2005 Theoretical formulation of collision rate and collision efficiency of hydrodynamically interacting cloud droplets in turbulent atmosphere. J. Atmos. Sci. 62 (7), 2433–2450.CrossRefGoogle Scholar
Wang, L.-P., Wexler, A.S. & Zhou, Y. 2000 Statistical mechanical description and modelling of turbulent collision of inertial particles. J. Fluid Mech. 415, 117–153.CrossRefGoogle Scholar
Yang, X., Huang, H. & Lu, X. 2015 Sedimentation of an oblate ellipsoid in narrow tubes. Phys. Rev. E 92 (6), 063009.CrossRefGoogle ScholarPubMed
Yin, X. & Koch, D.L. 2007 Hindered settling velocity and microstructure in suspensions of solid spheres with moderate Reynolds numbers. Phys. Fluids 19 (9), 093302.CrossRefGoogle Scholar
Zaidi, A.A. 2018 a Particle resolved direct numerical simulation of free settling particles for the study of effects of momentum response time on drag force. Powder Technol. 335, 222–234.CrossRefGoogle Scholar
Zaidi, A.A. 2018 b Particle velocity distributions and velocity fluctuations of non-Brownian settling particles by particle-resolved direct numerical simulation. Phys. Rev. E 98 (5), 053103.CrossRefGoogle Scholar
Zaidi, A.A. 2021 Domain size effects on particle microstructures settling in non-Stokes regime. In International Bhurban Conference on Applied Sciences and Technologies (IBCAST), Islamabad, Pakistan, pp. 748–753. IEEE.CrossRefGoogle Scholar
Zaidi, A.A., Tsuji, T. & Tanaka, T. 2014 Direct numerical simulation of finite sized particles settling for high Reynolds number and dilute suspension. Intl J. Heat Fluid Flow 50, 330–341.CrossRefGoogle Scholar
Zaidi, A.A., Tsuji, T. & Tanaka, T. 2015 Direct numerical simulations of inertial settling of non-Brownian particles. Korean J. Chem. Engng 32 (4), 617–628.CrossRefGoogle Scholar
Zastawny, M., Mallouppas, G., Zhao, F. & van Wachem, B. 2012 Derivation of drag and lift force and torque coefficients for non-spherical particles in flows. Intl J. Multiphase Flow 39, 227–239.CrossRefGoogle Scholar
Zhao, L., Gustavsson, K., Ni, R., Kramel, S., Voth, G.A., Andersson, H.I. & Mehlig, B. 2019 Passive directors in turbulence. Phys. Rev. Fluids 4 (5), 054602.CrossRefGoogle Scholar
Zhou, W., Chrust, M. & Dušek, J. 2017 Path instabilities of oblate spheroids. J. Fluid Mech. 833, 445–468.CrossRefGoogle Scholar
Zhou, W. & Dušek, J. 2015 Chaotic states and order in the chaos of the paths of freely falling and ascending spheres. Intl J. Multiphase Flow 75, 205–223.CrossRefGoogle Scholar