Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T23:34:23.126Z Has data issue: false hasContentIssue false
  • English
  • Français

Prograde, retrograde, and oscillatory modes in rotating Rayleigh–Bénard convection

Published online by Cambridge University Press:  13 October 2017

Susanne Horn Open the ORCID record for Susanne Horn [Opens in a new window]  and
Peter J. Schmid Open the ORCID record for Peter J. Schmid [Opens in a new window]
Susanne Horn*
Affiliation:
Department of Mathematics, Imperial College London, South Kensington Campus, London SW7 2AZ, UK Department of Earth, Planetary, and Space Sciences, University of California, Los Angeles, CA 90095, USA
Peter J. Schmid
Affiliation:
Department of Mathematics, Imperial College London, South Kensington Campus, London SW7 2AZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Rotating Rayleigh–Bénard convection is typified by a variety of regimes with very distinct flow morphologies that originate from several instability mechanisms. Here we present results from direct numerical simulations of three representative set-ups: first, a fluid with Prandtl number $Pr=6.4$, corresponding to water, in a cylinder with a diameter-to-height aspect ratio of 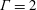$\unicode[STIX]{x1D6E4}=2$; second, a fluid with 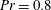$Pr=0.8$, corresponding to 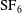$\text{SF}_{6}$ or air, confined in a slender cylinder with 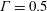$\unicode[STIX]{x1D6E4}=0.5$; and third, the main focus of this paper, a fluid with 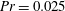$Pr=0.025$, corresponding to a liquid metal, in a cylinder with 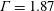$\unicode[STIX]{x1D6E4}=1.87$. The obtained flow fields are analysed using the sparsity-promoting variant of the dynamic mode decomposition (DMD). By means of this technique, we extract the coherent structures that govern the dynamics of the flow, as well as their associated frequencies. In addition, we follow the temporal evolution of single modes and present a criterion to identify their direction of travel, i.e. whether they are precessing prograde or retrograde. We show that for moderate 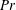$Pr$ a few dynamic modes suffice to accurately describe the flow. For large aspect ratios, these are wall-localised waves that travel retrograde along the periphery of the cylinder. Their DMD frequencies agree with the predictions of linear stability theory. With increasing Rayleigh number 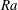$Ra$, the interior gradually fills with columnar vortices, and eventually a regular pattern of convective Taylor columns prevails. For small aspect ratios and close enough to onset, the dominant flow structures are body modes that can precess either prograde or retrograde. For 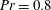$Pr=0.8$, DMD additionally unveiled the existence of so far unobserved low-amplitude oscillatory modes. Furthermore, we elucidate the multi-modal character of oscillatory convection in low-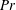$Pr$ fluids. Generally, more dynamic modes must be retained to accurately approximate the flow. Close to onset, the flow is purely oscillatory and the DMD reveals that these high-frequency modes are a superposition of oscillatory columns and cylinder-scale inertial waves. We find that there are coexisting prograde and retrograde modes, as well as quasi-axisymmetric torsional modes. For higher 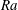$Ra$, the flow also becomes unstable to wall modes. These low-frequency modes can both coexist with the oscillatory modes, and also couple to them. However, the typical flow feature of rotating convection at moderate 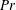$Pr$, the quasi-steady Taylor vortices, is entirely absent in low-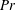$Pr$ flows.

JFM classification

Geophysical and Geological Flows: Rotating flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 831 , 25 November 2017 , pp. 182 - 211
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Brown, E., Fontenele Araujo, F., Funfschilling, D., Grossmann, S. & Lohse, D. 2006 Non-Oberbeck–Boussinesq effects in strongly turbulent Rayleigh–Bénard convection. J. Fluid Mech. 569, 409–445.CrossRefGoogle Scholar
Aurnou, J. M., Calkins, M. A., Cheng, J. S., Julien, K., King, E. M., Nieves, D., Soderlund, K. M. & Stellmach, S. 2015 Rotating convective turbulence in Earth and planetary cores. Phys. Earth Planet. Inter. 246, 52–71.Google Scholar
Aurnou, J. M. & King, E. M. 2017 The cross-over to magnetostrophic convection in planetary dynamo systems. Proc. R. Soc. Lond. A 473 (2199), 20160731.Google Scholar
Aurnou, J. M. & Olson, P. L. 2001 Experiments on Rayleigh–Bénard convection, magnetoconvection and rotating magnetoconvection in liquid gallium. J. Fluid Mech. 430, 283–307.CrossRefGoogle Scholar
Bertin, V., Grannan, A. M., Vogt, T., Horn, S. & Aurnou, J. M.2017 Rotating thermal convection in liquid gallium: multi-modal flow, absent steady columns. J. Fluid Mech. (in revision).Google Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Clarendon.Google Scholar
Chen, K. K., Tu, J. H. & Rowley, C. W. 2012 Variants of dynamic mode decomposition: boundary condition, Koopman, and Fourier analyses. J. Nonlinear Sci. 22 (6), 887–915.CrossRefGoogle Scholar
Cheng, J. S., Stellmach, S., Ribeiro, A., Grannan, A., King, E. M. & Aurnou, J. M. 2015 Laboratory-numerical models of rapidly rotating convection in planetary cores. Geophys. J. Intl 201 (1), 1–17.CrossRefGoogle Scholar
Chorin, A. J. 1967 A numerical method for solving incompressible viscous flow problems. J. Comput. Phys. 2 (1), 12–26.Google Scholar
Christensen, U. R. 2011 Geodynamo models: tools for understanding properties of Earth’s magnetic field. Phys. Earth Planet. Inter. 187 (3), 157–169.Google Scholar
Clune, T. & Knobloch, E. 1993 Pattern selection in rotating convection with experimental boundary conditions. Phys. Rev. E 47 (4), 2536–2550.Google ScholarPubMed
Ecke, R. E. & Niemela, J. J. 2014 Heat transport in the geostrophic regime of rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 113 (11), 114301.Google Scholar
Ecke, R. E., Zhong, Fang & Knobloch, E. 1992 Hopf bifurcation with broken reflection symmetry in rotating Rayleigh–Bénard convection. Europhys. Lett. 19 (3), 177.Google Scholar
Favier, B., Silvers, L. J. & Proctor, M. R. E. 2014 Inverse cascade and symmetry breaking in rapidly rotating Boussinesq convection. Phys. Fluids 26 (9), 096605.Google Scholar
Finlay, C. C. & Jackson, A. 2003 Equatorially dominated magnetic field change at the surface of Earth’s core. Science 300 (5628), 2084–2086.Google Scholar
Gastine, T., Wicht, J. & Aubert, J. 2016 Scaling regimes in spherical shell rotating convection. J. Fluid Mech. 808, 690–732.Google Scholar
Gillet, N., Jault, D., Canet, E. & Fournier, A. 2010 Fast torsional waves and strong magnetic field within the Earth’s core. Nature 465 (7294), 74–77.Google Scholar
Gizon, L. & Birch, A. C. 2005 Local helioseismology. Living Reviews Solar Phys. 2 (1), 1–131.CrossRefGoogle Scholar
Goldstein, H. F., Knobloch, E., Mercader, I. & Net, M. 1993 Convection in a rotating cylinder. Part 1. Linear theory for moderate Prandtl numbers. J. Fluid Mech. 248, 583–604.CrossRefGoogle Scholar
Goldstein, H. F., Knobloch, E., Mercader, I. & Net, M. 1994 Convection in a rotating cylinder. Part 2. Linear theory for low Prandtl numbers. J. Fluid Mech. 262, 293–324.Google Scholar
Grooms, I., Julien, K., Weiss, J. B. & Knobloch, E. 2010 Model of convective Taylor columns in rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 104, 224501.Google Scholar
Guervilly, C., Hughes, D. W. & Jones, C. A. 2014 Large-scale vortices in rapidly rotating Rayleigh–Bénard convection. J. Fluid Mech. 758, 407–435.Google Scholar
He, X., Funfschilling, D., Nobach, H., Bodenschatz, E. & Ahlers, G. 2012 Transition to the ultimate state of turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 108, 024502.Google Scholar
Herrmann, J. & Busse, F. H. 1993 Asymptotic theory of wall-attached convection in a rotating fluid layer. J. Fluid Mech. 255, 183–194.Google Scholar
Hori, K., Jones, C. A. & Teed, R. J. 2015 Slow magnetic Rossby waves in the Earth’s core. Geophys. Res. Lett. 42 (16), 6622–6629.Google Scholar
Horn, S. & Shishkina, O. 2014 Rotating non-Oberbeck–Boussinesq Rayleigh–Bénard convection in water. Phys. Fluids 26 (5), 055111.Google Scholar
Horn, S. & Shishkina, O. 2015 Toroidal and poloidal energy in rotating Rayleigh–Bénard convection. J. Fluid Mech. 762, 232–255.CrossRefGoogle Scholar
Horn, S., Shishkina, O. & Wagner, C. 2013 On non-Oberbeck–Boussinesq effects in three-dimensional Rayleigh–Bénard convection in glycerol. J. Fluid Mech. 724, 175–202.Google Scholar
Jones, C. A. 2011 Planetary magnetic fields and fluid dynamos. Annu. Rev. Fluid Mech. 43, 583–614.Google Scholar
Jovanović, M. R., Schmid, P. J. & Nichols, J. W. 2014 Sparsity-promoting dynamic mode decomposition. Phys. Fluids 26 (2), 024103.Google Scholar
Julien, K., Knobloch, E., Rubio, A. M. & Vasil, G. M. 2012a Heat transport in low-Rossby-number Rayleigh–Bénard convection. Phys. Rev. Lett. 109 (25), 254503.CrossRefGoogle ScholarPubMed
Julien, K., Legg, S., McWilliams, J. & Werne, J. 1996 Rapidly rotating turbulent Rayleigh–Bénard convection. J. Fluid Mech. 322, 243–273.Google Scholar
Julien, K., Rubio, A. M., Grooms, I. & Knobloch, E. 2012b Statistical and physical balances in low Rossby number Rayleigh–Bénard convection. Geophys. Astrophys. Fluid Dyn. 106 (4–5), 392–428.CrossRefGoogle Scholar
King, E. M. & Aurnou, J. M. 2013 Turbulent convection in liquid metal with and without rotation. PNAS 110 (17), 6688–6693.CrossRefGoogle ScholarPubMed
King, E. M., Stellmach, S. & Aurnou, J. M. 2012 Heat transfer by rapidly rotating Rayleigh–Bénard convection. J. Fluid Mech. 691, 568–582.CrossRefGoogle Scholar
King, E. M., Stellmach, S., Noir, J., Hansen, U. & Aurnou, J. M. 2009 Boundary layer control of rotating convection systems. Nature 457, 301–304.CrossRefGoogle ScholarPubMed
Kunnen, R. P. J., Clercx, H. J. H. & Geurts, B. J. 2008 Breakdown of large-scale circulation in turbulent rotating convection. Europhys. Lett. 84 (2), 24001.CrossRefGoogle Scholar
Kunnen, R. P. J., Clercx, H. J. H. & van Heijst, G. J. F. 2013 The structure of sidewall boundary layers in confined rotating Rayleigh–Bénard convection. J. Fluid Mech. 727, 509–532.Google Scholar
Kunnen, R. P. J., Corre, Y. & Clercx, H. J. H. 2014 Vortex plume distribution in confined turbulent rotating convection. Europhys. Lett. 104 (5), 54002.Google Scholar
Kunnen, R. P. J., Geurts, B. J. & Clercx, H. J. H. 2010 Experimental and numerical investigation of turbulent convection in a rotating cylinder. J. Fluid Mech. 626, 445–476.Google Scholar
Kunnen, R. P. J., Ostilla-Mónico, R., van der Poel, E. P., Verzicco, R. & Lohse, D. 2016 Transition to geostrophic convection: the role of the boundary conditions. J. Fluid Mech. 799, 413–432.CrossRefGoogle Scholar
Kuo, E. Y. & Cross, M. C. 1993 Traveling-wave wall states in rotating Rayleigh–Bénard convection. Phys. Rev. E 47 (4), R2245–R2248.Google ScholarPubMed
Liu, Y. & Ecke, R. E. 1997 Heat transport scaling in turbulent Rayleigh–Bénard convection: effects of rotation and Prandtl number. Phys. Rev. Lett. 79 (12), 2257–2260.Google Scholar
Liu, Y. & Ecke, R. E. 1999 Nonlinear traveling waves in rotating Rayleigh–Bénard convection: stability boundaries and phase diffusion. Phys. Rev. E 59 (4), 4091.Google Scholar
Ning, L. & Ecke, R. E. 1993 Rotating Rayleigh–Bénard convection: aspect-ratio dependence of the initial bifurcations. Phys. Rev. E 47 (5), 3326.Google Scholar
Roberts, P. H. & Aurnou, J. M. 2012 On the theory of core-mantle coupling. Geophys. Astrophys. Fluid Dyn. 106 (2), 157–230.Google Scholar
Roberts, P. H. & King, E. M. 2013 On the genesis of the earth’s magnetism. Rep. Prog. Phys. 76 (9), 096801.CrossRefGoogle ScholarPubMed
Rossby, H. T. 1969 A study of Bénard convection with and without rotation. J. Fluid Mech. 36, 309–335.Google Scholar
Rowley, C. W., Mezić, I., Bagheri, S., Schlatter, P. & Henningson, D. S. 2009 Spectral analysis of nonlinear flows. J. Fluid Mech. 641, 115–127.Google Scholar
Rubio, A. M., Julien, K., Knobloch, E. & Weiss, J. B. 2014 Upscale energy transfer in three-dimensional rapidly rotating turbulent convection. Phys. Rev. Lett. 112 (14), 144501.Google Scholar
Sakai, S. 1997 The horizontal scale of rotating convection in the geostrophic regime. J. Fluid Mech. 333, 85–95.Google Scholar
Sánchez, J., Garcia, F. & Net, M. 2016 Critical torsional modes of convection in rotating fluid spheres at high Taylor numbers. J. Fluid Mech. 791, R1.Google Scholar
Schmid, P. J. 2010 Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 656, 5–28.CrossRefGoogle Scholar
Schmid, P. J., Li, L., Juniper, M. P. & Pust, O. 2011 Applications of the dynamic mode decomposition. Theor. Comput. Fluid Dyn. 25 (1–4), 249–259.Google Scholar
Schumacher, J., Bandaru, V., Pandey, A. & Scheel, J. D. 2016 Transitional boundary layers in low-Prandtl-number convection. Phys. Rev. Fluids 1, 084402.Google Scholar
Schumacher, J., Götzfried, P. & Scheel, J. D. 2015 Enhanced enstrophy generation for turbulent convection in low-Prandtl-number fluids. PNAS 112 (31), 9530–9535.Google Scholar
Shishkina, O. & Horn, S. 2016 Thermal convection in inclined cylindrical containers. J. Fluid Mech. 790, R3.Google Scholar
Shishkina, O., Horn, S., Wagner, S. & Ching, E. S. C. 2015 Thermal boundary layer equation for turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 114 (11), 114302.Google Scholar
Shishkina, O., Stevens, R. J. A. M., Grossmann, S. & Lohse, D. 2010 Boundary layer structure in turbulent thermal convection and its consequences for the required numerical resolution. New J. Phys. 12 (7), 075022.Google Scholar
Shishkina, O. & Wagner, S. 2016 Prandtl-number dependence of heat transport in laminar horizontal convection. Phys. Rev. Lett. 116 (2), 024302.Google Scholar
Shishkina, O., Wagner, S. & Horn, S. 2014 Influence of the angle between the wind and the isothermal surfaces on the boundary layer structures in turbulent thermal convection. Phys. Rev. E 89 (3), 033014.Google Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures. I-Coherent structures. II-Symmetries and transformations. III-Dynamics and scaling. Q. Appl. Maths XLV (3), 561–590.Google Scholar
Sprague, M., Julien, K., Knobloch, E. & Werne, J. 2006 Numerical simulation of an asymptotically reduced system for rotationally constrained convection. J. Fluid Mech. 551, 141–174.CrossRefGoogle Scholar
Stellmach, S., Lischper, M., Julien, K., Vasil, G., Cheng, J. S., Ribeiro, A., King, E. M. & Aurnou, J. M. 2014 Approaching the asymptotic regime of rapidly rotating convection: boundary layers versus interior dynamics. Phys. Rev. Lett. 113 (25), 254501.CrossRefGoogle ScholarPubMed
Stevens, R. J. A. M., Clercx, H. J. H. & Lohse, D. 2010 Optimal Prandtl number for heat transfer in rotating Rayleigh–Bénard convection. New J. Phys. 12 (7), 075005.Google Scholar
Stevens, R. J. A. M., Clercx, H. J. H. & Lohse, D. 2013 Heat transport and flow structure in rotating Rayleigh–Bénard convection. Eur. J. Mech. (B/Fluids) 40, 41–49.Google Scholar
Stevens, R. J. A. M., Lohse, D. & Verzicco, R. 2011 Prandtl and Rayleigh number dependence of heat transport in high Rayleigh number thermal convection. J. Fluid Mech. 688 (1), 31–43.Google Scholar
Stevens, R. J. A. M., Zhong, J-Q., Clercx, H. J. H., Ahlers, G. & Lohse, D. 2009 Transitions between turbulent states in rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 103, 024503.Google Scholar
Tu, J. H., Rowley, C. W., Luchtenburg, D. M., Brunton, S. L. & Kutz, J. N. 2014 On dynamic mode decomposition: theory and applications. J. Comput. Dyn. 1, 391–421.Google Scholar
Weiss, S. & Ahlers, G. 2011a Heat transport by turbulent rotating Rayleigh–Bénard convection and its dependence on the aspect ratio. J. Fluid Mech. 684 (407), 205.Google Scholar
Weiss, S. & Ahlers, G. 2011b The large-scale flow structure in turbulent rotating Rayleigh–Bénard convection. J. Fluid Mech. 688, 461.Google Scholar
Weiss, S., Stevens, R. J. A. M., Zhong, J.-Q., Clercx, H. J. H., Lohse, D. & Ahlers, G. 2010 Finite-size effects lead to supercritical bifurcations in turbulent rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 105, 224501.Google Scholar
Zhang, K. & Liao, X. 2009 The onset of convection in rotating circular cylinders with experimental boundary conditions. J. Fluid Mech. 622, 63–73.CrossRefGoogle Scholar
Zhang, K., Liao, X. & Busse, F. H. 2007 Asymptotic theory of inertial convection in a rotating cylinder. J. Fluid Mech. 575, 449–471.CrossRefGoogle Scholar
Zhong, F., Ecke, R. E. & Steinberg, V. 1991 Rotating Rayleigh–Bénard convection: Küppers–Lortz transition. Physica D 51 (1), 596–607.Google Scholar
Zhong, F., Ecke, R. E. & Steinberg, V. 1993 Rotating Rayleigh–Bénard convection: asymmetric modes and vortex states. J. Fluid Mech. 249, 135–159.Google Scholar
Zhong, J.-Q. & Ahlers, G. 2010 Heat transport and the large-scale circulation in rotating turbulent Rayleigh–Bénard convection. J. Fluid Mech. 665, 300–333.Google Scholar

Horn and Schmid supplementary movie 1

Supplementary movie to figure 2. DNS results showing the temperature and the azimuthal velocity for Pr = 6.4, Ra = 1.55 × 105. The movie shows 500 time units.

Download Horn and Schmid supplementary movie 1(Video)
Video 28.6 MB

Horn and Schmid supplementary movie 2

Supplementary movie to figure 2. DNS results showing the temperature and the azimuthal velocity for Pr = 6.4, Ra = 6.49 × 105. The movie shows 500 time units.

Download Horn and Schmid supplementary movie 2(Video)
Video 27 MB

Horn and Schmid supplementary movie 3

Supplementary movie to figure 2. DNS results showing the temperature and the azimuthal velocity for Pr = 6.4, Ra = 2.60 × 106. The movie shows 500 time units.

Download Horn and Schmid supplementary movie 3(Video)
Video 42.9 MB

Horn and Schmid supplementary movie 4

Supplementary movie to figure 3. DNS results for Pr = 0.8 showing the temperature for Ro = 0.3 (left) and Ro = 0.5 (right). The movie shows 1000 time units.

Download Horn and Schmid supplementary movie 4(Video)
Video 10.2 MB

Horn and Schmid supplementary movie 5

Supplementary movie to figure 4. Oscillatory DMD mode for Pr = 0.8 and Ro = 0.5. The movie shows the evolution over 500 time units.

Download Horn and Schmid supplementary movie 5(Video)
Video 6 MB

Horn and Schmid supplementary movie 6

Supplementary movie to figure 8. DNS results showing the temperature and the azimuthal velocity for Pr = 0.025, Ra = 8.1 × 105, Ek = 2 × 10-5. The movie shows 50 time units.

Download Horn and Schmid supplementary movie 6(Video)
Video 22.4 MB

Horn and Schmid supplementary movie 7

Supplementary movie to figure 9. DNS results showing the temperature and the azimuthal velocity for Pr = 0.025, Ra = 8.0 × 106, Ek = 5 × 10-6. The movie shows 50 time units.

Download Horn and Schmid supplementary movie 7(Video)
Video 20.5 MB

Horn and Schmid supplementary movie 8

Supplementary movie to figure 12. Retrograde DMD mode for Pr = 0.025, Ra = 8.1 × 105, Ek = 2 × 10-5. The movie shows the evolution over 50 time units.

Download Horn and Schmid supplementary movie 8(Video)
Video 22.4 MB

Horn and Schmid supplementary movie 9

Supplementary movie to figure 13. Prograde DMD mode for Pr = 0.025, Ra = 8.1 × 105, Ek = 2 × 10-5. The movie shows the evolution over 50 time units.

Download Horn and Schmid supplementary movie 9(Video)
Video 23.7 MB

Horn and Schmid supplementary movie 10

Supplementary movie to figure 14. Axisymmetric DMD mode for Pr = 0.025, Ra = 8.1 × 105, Ek = 2 × 10-5. The movie shows the evolution over 50 time units.

Download Horn and Schmid supplementary movie 10(Video)
Video 20.4 MB

Horn and Schmid supplementary movie 11

Supplementary movie to figure 15. Retrograde m = 4 DMD mode for Pr = 0.025, Ra = 8.0 × 106, Ek = 5 × 10-6. The movie shows the evolution over 50 time units.

Download Horn and Schmid supplementary movie 11(Video)
Video 12.3 MB

Horn and Schmid supplementary movie 12

Supplementary movie to figure 16. Coupled m = 5 DMD mode for Pr = 0.025, Ra = 8.0 × 106, Ek = 5 × 10-6. The movie shows the evolution over 50 time units.

Download Horn and Schmid supplementary movie 12(Video)
Video 19.7 MB

Horn and Schmid supplementary movie 13

Supplementary movie to figure 17. Oscillatory DMD mode for Pr = 0.025, Ra = 8.0 × 106, Ek = 5 × 10-6. The movie shows the evolution over 50 time units.

Download Horn and Schmid supplementary movie 13(Video)
Video 34 MB