Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-17T11:26:33.416Z Has data issue: false hasContentIssue false
  • English
  • Français

Primary instability of a shear-thinning film flow down an incline: experimental study

Published online by Cambridge University Press:  24 May 2017

M. H. Allouche ,
V. Botton ,
S. Millet ,
D. Henry ,
S. Dagois-Bohy Open the ORCID record for S. Dagois-Bohy [Opens in a new window] ,
B. Güzel  and
H. Ben Hadid
M. H. Allouche
Affiliation:
Laboratoire de Mécanique des Fluides et d’Acoustique, CNRS/Université de Lyon, École Centrale de Lyon/Université Lyon 1/INSA de Lyon, ECL, 36 avenue Guy de Collongue, 69134 Ecully CEDEX, France INSA Euro-Méditerranée, Université Euro-Méditerranéenne de Fès, Route de Meknès, BP51, Fez, Morocco
V. Botton
Affiliation:
Laboratoire de Mécanique des Fluides et d’Acoustique, CNRS/Université de Lyon, École Centrale de Lyon/Université Lyon 1/INSA de Lyon, ECL, 36 avenue Guy de Collongue, 69134 Ecully CEDEX, France INSA Euro-Méditerranée, Université Euro-Méditerranéenne de Fès, Route de Meknès, BP51, Fez, Morocco
S. Millet
Affiliation:
Laboratoire de Mécanique des Fluides et d’Acoustique, CNRS/Université de Lyon, École Centrale de Lyon/Université Lyon 1/INSA de Lyon, ECL, 36 avenue Guy de Collongue, 69134 Ecully CEDEX, France
D. Henry
Affiliation:
Laboratoire de Mécanique des Fluides et d’Acoustique, CNRS/Université de Lyon, École Centrale de Lyon/Université Lyon 1/INSA de Lyon, ECL, 36 avenue Guy de Collongue, 69134 Ecully CEDEX, France
S. Dagois-Bohy*
Affiliation:
Laboratoire de Mécanique des Fluides et d’Acoustique, CNRS/Université de Lyon, École Centrale de Lyon/Université Lyon 1/INSA de Lyon, ECL, 36 avenue Guy de Collongue, 69134 Ecully CEDEX, France
B. Güzel
Affiliation:
Laboratoire de Mécanique des Fluides et d’Acoustique, CNRS/Université de Lyon, École Centrale de Lyon/Université Lyon 1/INSA de Lyon, ECL, 36 avenue Guy de Collongue, 69134 Ecully CEDEX, France Yildiz Technical University, Department of Naval Architecture and Marine Engineering, Marine Machinery, 34349 Yildiz, Istanbul, Turkey
H. Ben Hadid
Affiliation:
Laboratoire de Mécanique des Fluides et d’Acoustique, CNRS/Université de Lyon, École Centrale de Lyon/Université Lyon 1/INSA de Lyon, ECL, 36 avenue Guy de Collongue, 69134 Ecully CEDEX, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The main objective of this work is to study experimentally the primary instability of non-Newtonian film flows down an inclined plane. We focus on low-concentration shear-thinning aqueous solutions obeying the Carreau law. The experimental study essentially consists of measuring wavelengths in marginal conditions, which yields the primary stability threshold for a given slope. 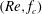The experimental results for neutral curves presented in the $(Re,f_{c})$ and 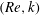$(Re,k)$ planes (where 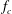$f_{c}$ is the driving frequency, 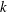$k$ is the wavenumber and 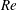$Re$ is the Reynolds number) are in good agreement with the numerical results obtained by a resolution of the generalized Orr–Sommerfeld equation. The long-wave asymptotic extension of our results is consistent with former theoretical predictions of the critical Reynolds number. This is the first experimental evidence of the destabilizing effect of the shear-thinning behaviour in comparison with the Newtonian case: the critical Reynolds number is smaller, and the ratio between the critical wave celerity and the flow velocity at the free surface is larger.

JFM classification

Instability: Instability Non-Newtonian Flows: Non-Newtonian Flows Interfacial Flows (free surface): Thin films
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 821 , 25 June 2017 , R1
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allouche, M. H., Botton, V., Henry, D., Millet, S., Usha, R. & Ben Hadid, H. 2015 Experimental determination of the viscosity at very low shear rate for shear thinning fluids by electrocapillarity. J. Non-Newtonian Fluid Mech. 215, 60–69.Google Scholar
Amaouche, M., Djema, A. & Bourdache, L. 2009 A modified Shkadov’s model for thin film flow of a power law fluid over an inclined surface. C. R. Méc. 337 (1), 48–52.CrossRefGoogle Scholar
Argyriadi, K., Serifi, K. & Bontozoglou, V. 2004 Nonlinear dynamics of inclined films under low-frequency forcing. Phys. Fluids 16 (7), 2457–2468.CrossRefGoogle Scholar
Benchabane, A. & Bekkour, K. 2008 Rheological properties of carboxymethyl cellulose (CMC) solutions. Colloid Polym. Sci. 286 (10), 1173–1180.CrossRefGoogle Scholar
Benjamin, T. B. 1957 Wave formation in laminar flow down an inclined plane. J. Fluid Mech. 2 (06), 554–573.Google Scholar
Chambon, G., Ghemmour, A. & Laigle, D. 2009 Gravity-driven surges of a viscoplastic fluid: an experimental study. J. Non-Newtonian Fluid Mech. 158, 54–62.CrossRefGoogle Scholar
Chambon, G., Ghemmour, A. & Naaim, M. 2014 Experimental investigation of viscoplastic free-surface flows in a steady uniform regime. J. Fluid Mech. 754, 332–364.CrossRefGoogle Scholar
Coussot, P. 1994 Steady, laminar flow of concentrated mud suspensions in open channel. J. Hydraul. Res. 32 (4), 535–559.Google Scholar
Dandapat, B. S. & Mukhopadhyay, A. 2001 Waves on a film of power-law fluid flowing down an inclined plane at moderate Reynolds number. Fluid Dyn. Res. 29 (3), 199–220.Google Scholar
Denner, F., Pradas, M., Charogiannis, A., Markides, C. N., van Wachem, B. G. M. & Kalliadasis, S. 2016 Self-similarity of solitary waves on inertia-dominated falling liquid films. Phys. Rev. E 93, 033121.Google Scholar
Escudier, M. P., Gouldson, I. W., Pereira, A. S., Pinho, F. T. & Poole, R. J. 2001 On the reproducibility of the rheology of shear-thinning liquids. J. Non-Newtonian Fluid Mech. 97 (2), 99–124.Google Scholar
Fernández-Nieto, E. D., Noble, P. & Vila, J.-P. 2010 Shallow water equations for non-Newtonian fluids. J. Non-Newtonian Fluid Mech. 165 (13), 712–732.Google Scholar
Forterre, Y. & Pouliquen, O. 2003 Long-surface-wave instability in dense granular flows. J. Fluid Mech. 486, 21–50.Google Scholar
Georgantaki, A., Vatteville, J., Vlachogiannis, M. & Bontozoglou, V. 2011 Measurements of liquid film flow as a function of fluid properties and channel width: evidence for surface-tension-induced long-range transverse coherence. Phys. Rev. E 84 (2), 026325.Google Scholar
Huang, X. & Garcia, M. H. 1998 A Herschel–Bulkley model for mud flow down a slope. J. Fluid Mech. 374, 305–333.CrossRefGoogle Scholar
Jeong, S. W. 2010 Grain size dependent rheology on the mobility of debris flows. Geosci. J. 14 (4), 359–369.CrossRefGoogle Scholar
Jouvet, G., Picasso, M., Rappaz, J., Huss, M. & Funk, M. 2011 Modelling and numerical simulation of the dynamics of glaciers including local damage effects. Math. Modelling Natural Phenom. 6 (5), 263–280.CrossRefGoogle Scholar
Kalliadasis, S., Ruyer-Quil, C., Scheid, B. & Velarde, M. G. 2011 Falling Liquid Films. Springer.Google Scholar
Kapitza, P. L. & Kapitza, S. P. 1949 Wave flow of thin layers of viscous liquids. Part III. Experimental research of a wave flow regime. Zh. Eksp. Teor. Fiz. 19, 105–120.Google Scholar
Liu, J., Paul, J. D. & Gollub, J. P. 1993 Measurements of the primary instabilities of film flows. J. Fluid Mech. 250, 69–101.Google Scholar
Millet, S., Botton, V., Rousset, F. & Ben Hadid, H. 2008 Wave celerity on a shear-thinning fluid film flowing down an incline. Phys. Fluids 20 (3), 031701.CrossRefGoogle Scholar
Moisy, F., Rabaud, M. & Salsac, K. 2009 A synthetic schlieren method for the measurement of the topography of a liquid interface. Exp. Fluids 46 (6), 1021–1036.Google Scholar
Ng, C.-O. & Mei, C. C. 1994 Roll waves on a shallow layer of mud modeled as a power-law fluid. J. Fluid Mech. 263, 151–183.Google Scholar
Noble, P. & Vila, J.-P. 2013 Thin power-law film flow down an inclined plane: consistent shallow-water models and stability under large-scale perturbations. J. Fluid Mech. 735, 29–60.Google Scholar
Rodd, A. B., Dunstan, D. E. & Boger, D. V. 2000 Characterisation of xanthan gum solutions using dynamic light scattering and rheology. Carbohydrate Polym. 42 (2), 159–174.Google Scholar
Rousset, F., Millet, S., Botton, V. & Ben Hadid, H. 2007 Temporal stability of Carreau fluid flow down an incline. J. Fluids Engng Trans. ASME 129 (7), 913–920.Google Scholar
Ruyer-Quil, C., Chakraborty, S. & Dandapat, B. S. 2012 Wavy regime of a power-law film flow. J. Fluid Mech. 692, 220–256.Google Scholar
Smith, M. K. 1990 The mechanism for the long-wave instability in thin liquid films. J. Fluid Mech. 217, 469–485.Google Scholar
Takamura, K., Fischer, H. & Morrow, N. R. 2012 Physical properties of aqueous glycerol solutions. J. Petrol. Sci. Engng 9899, 50–60.Google Scholar
Vlachogiannis, M., Samandas, A., Leontidis, V. & Bontozoglou, V. 2010 Effect of channel width on the primary instability of inclined film flow. Phys. Fluids 22 (1), 012106.CrossRefGoogle Scholar
Weinstein, S. J. 1990 Wave propagation in the flow of shear-thinning fluids down an incline. AIChE J. 36 (12), 1873–1889.Google Scholar
Whitham, G. B. 2011 Linear and Nonlinear Waves. Wiley.Google Scholar
Yih, C.-S. 1963 Stability of liquid flow down an inclined plane. Phys. Fluids 6 (3), 321–334.Google Scholar