Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-24T14:14:25.789Z Has data issue: false hasContentIssue false
  • English
  • Français

Premixed flame–wall interaction in a narrow channel: impact of wall thermal conductivity and heat losses

Published online by Cambridge University Press:  28 September 2018

K. Bioche ,
L. Vervisch  and
G. Ribert
K. Bioche
Affiliation:
CORIA – CNRS, Normandie Université, INSA de Rouen, Technopôle du Madrillet, BP 8, 76801 Saint-Etienne-du-Rouvray, France
L. Vervisch*
Affiliation:
CORIA – CNRS, Normandie Université, INSA de Rouen, Technopôle du Madrillet, BP 8, 76801 Saint-Etienne-du-Rouvray, France
G. Ribert
Affiliation:
CORIA – CNRS, Normandie Université, INSA de Rouen, Technopôle du Madrillet, BP 8, 76801 Saint-Etienne-du-Rouvray, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The flow physics controlling the stabilisation of a methane/air laminar premixed flame in a narrow channel (internal width 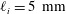$\ell _{i}=5~\text{mm}$) is revisited from numerical simulations. Combustion is described with complex chemistry and transport properties, along with a coupled simulation of heat transfer at and within the wall. To conduct a thorough analysis of the flame–wall interaction, the steady flame is obtained after applying a procedure to find the inlet mass flow rate that exactly matches the flame mass burning rate. The response of the premixed flame shape to various operating conditions is then analysed in terms of flame propagation velocity and flow topology in the vicinity of the reactive front. We focus on the interrelations between the flame speed, the configuration taken by the flame surface, the flow deviation induced by the heat released and the fluxes at the wall. Compared to an adiabatic flame, the flame speed increases with edge-flame quenching at an isothermal cold wall in the absence of a boundary layer, decreases with a boundary layer, to increase again with heat-transfer coupling within the wall. A regime diagram is proposed to delineate between flame shapes in order to build a classification versus heat-transfer properties. Under a small level of convective heat transfer with the ambient air surrounding the channel, the larger the thermal conductivity in the solid, the faster the reaction zone propagates in the vicinity of the wall, leaving the centreline reaction zone behind. The premixed flame front is then concave towards the fresh gases on the axis of symmetry (so-called tulip flame) with a flame speed higher than in the adiabatic case. Increasing the heat loss at the wall through convection with ambient air, the flame shape becomes convex (mushroom flame) and the flame speed decreases below its adiabatic level. Scaling laws are provided for the flame speed under these various regimes. Mesh resolution was calibrated, with and without heat loss, from simulations of one-dimensional detailed chemistry flames, leading to mesh resolution of 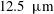$12.5~\unicode[STIX]{x03BC}\text{m}$ for detailed chemistry and 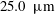$25.0~\unicode[STIX]{x03BC}\text{m}$ with a skeleton mechanism. The quality of the resolution was also assessed from multi-physics budgets derived from first principles, involving upstream-flame heat retrocession by the wall leading to flow acceleration, budgets bringing physical insights into flame/wall interaction. Additional overall mesh convergence tests of the multi-physics solution would have been desirable, but were not conducted due to the high computing cost of these fully compressible simulations, hence also solving for the acoustic field with low convective velocities.

JFM classification

Reacting Flows: Combustion Reacting Flows: Flames Reacting Flows: Laminar reacting flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 856 , 10 December 2018 , pp. 5 - 35
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bai, B., Chen, Z., Zhang, H. & Chen, S. 2013 Flame propagation in a tube with wall quenching of radicals. Combust. Flame 160 (12), 2810–2819.Google Scholar
Bianco, F., Chibbaro, S. & Legros, G. 2015 Low-dimensional modeling of flame dynamics in heated microchannels. Chem. Engng Sci. 122, 533–544.Google Scholar
Boehman, A. L. 1998 Radiation heat transfer in catalytic monoliths. AIChE J. 44 (12), 2745–2755.Google Scholar
Bouheraoua, L., Domingo, P. & Ribert, G. 2017 Large-eddy simulation of a supersonic lifted jet flame: analysis of the turbulent flame base. Combust. Flame 179, 199–218.Google Scholar
Bucci, M., Robinet, J.-M. & Chibbaro, S. 2016 Global stability analysis of 3D micro-combustion model. Combust. Flame 167, 132–148.Google Scholar
Chakraborty, S., Mukhopadhyay, A. & Sen, S. 2008 Interaction of Lewis number and heat loss effects for a laminar premixed flame propagating in a channel. Intl J. Therm. Sci. 47 (1), 84–92.Google Scholar
Chigier, N. & Gemci, T. 2003 A review of micro propulsion technology. In 41st Aerospace Sciences Meeting and Exhibit, p. 670. AIAA.Google Scholar
Choi, C. W. & Puri, I. 2003 Response of flame speed to positively and negatively curved premixed flames. Combust. Theor. Model. 7, 205–220.Google Scholar
Clavin, P. 1994 Premixed combustion and gasdynamics. Annu. Rev. Fluid Mech. 26, 321–352.Google Scholar
Clavin, P., Pelcé, P. & He, L. 1990 One-dimensional vibratory instability of planar flames propagating in tubes. J. Fluid Mech. 216, 299–322.Google Scholar
Clavin, P. & Searby, G. 2016 Combustion Waves and Fronts in Flows. Cambridge University Press.Google Scholar
Curtiss, C. F. & Hirschfelder, J. O. 1949 Transport properties of multicomponent gas mixtures. J. Chem. Phys. 17 (6), 550–555.Google Scholar
Davy, H. 1817 Some researches on flame. Phil. Trans. R. Soc. Lond. A 107, 45–76.Google Scholar
Domingo, P. & Vervisch, L. 2017 DNS and approximate deconvolution as a tool to analyse one-dimensional filtered flame sub-grid scale modeling. Combust. Flame 177, 109–122.Google Scholar
Domingo, P., Vervisch, L. & Veynante, D. 2008 Large-Eddy Simulation of a lifted methane–air jet flame in a vitiated coflow. Combust. Flame 152 (3), 415–432.Google Scholar
Douglas, J. Jr 1955 On the numerical integration of ∂ 2 u∂x 2 + ∂ 2 u∂y 2 = ∂u∂t by implicit methods. J. Soc. Ind. Appl. Maths 3 (1), 42–65.Google Scholar
Duchaine, F., Corpron, A., Pons, L., Moureau, V., Nicoud, F. & Poinsot, T. 2009 Development and assessment of a coupled strategy for conjugate heat transfer with large eddy simulation: application to a cooled turbine blade. Intl J. Heat Fluid Flow 30 (6), 1129–1141.Google Scholar
Ducros, F., Ferrand, V., Nicoud, F., Weber, C., Darracq, D., Gacherieu, C. & Poinsot, T. 1999 Large-eddy simulation of the shock/turbulence interaction. J. Comput. Phys. 152 (2), 517–549.Google Scholar
Emanuel, G. 1994 Analytical Fluid Dynamics. CRC Press.Google Scholar
Fernandez-Pello, A. C. 2002 Micropower generation using combustion: issues and approaches. Proc. Combust. Inst. 29 (1), 883–899.Google Scholar
Frenklach, M., Wang, H., Yu, C.-L., Goldenberg, M., Bowman, C. T., Hanson, R. K., Davidson, D. F., Chang, E. J., Smith, G. P., Golden, D. M., Gardiner, W. C. & Lissianski, V.1995 Gri-mech—an Optimized Detailed Chemical Reaction Mechanism for Methane Combustion. Tech. Rep. Gas Research Institute, Chicago, IL, report no. GRI-95/0058.Google Scholar
Ganter, S., Heinrich, A., Meier, T., Kuenne, G., Jainski, C., Rissmann, M., Dreizler, A. & Janicka, J. 2017 Numerical analysis of laminar methane–air side-wall-quenching. Combust. Flame 186, 299–310.Google Scholar
Gauthier, G. P. & Bergthorson, J. M. 2016 Effect of external heat loss on the propagation and quenching of flames in small heat-recirculating tubes. Combust. Flame 173, 27–38.Google Scholar
Gauthier, G. P., Watson, G. M. G. & Bergthorson, J. M. 2012 An evaluation of numerical models for temperature-stabilized CH4/air flames in a small channel. Combust. Sci. Technol. 184 (6), 850–868.Google Scholar
Giovangigli, V. 1999 Multicomponent flow modeling. In Modeling and Simulation in Science, Engineering and Technology, p. 321. Birkhäuser, Springer.Google Scholar
Gonzalez, M., Borghi, R. & Saouab, A. 1992 Interaction of a flame front with its self-generated flow in an enclosure: the ‘tulip flame’ phenomenon. Combust. Flame 88 (2), 201–220.Google Scholar
Goodwin, D.2009 Cantera: an object-oriented software toolkit for chemical kinetics, thermodynamics, and transport processes, http://code.google.com/p/cantera.Google Scholar
Jameson, A., Schmidt, W. & Turkel, E. 1981 Numerical solution of the euler equations by finite volume methods using Runge–Kutta time stepping schemes. In 14th Fluid and Plasma Dynamics Conference, p. 1259. AIAA.Google Scholar
Jaouen, N., Vervisch, L. & Domingo, P. 2017a Auto-thermal reforming (ATR) of natural gas: an automated derivation of optimised reduced chemical schemes. Proc. Combust. Inst. 36 (3), 3321–3330.Google Scholar
Jaouen, N., Vervisch, L., Domingo, P. & Ribert, G. 2017b Automatic reduction and optimisation of chemistry for turbulent combustion modeling: impact of the canonical problem. Combust. Flame 175, 60–79.Google Scholar
Jarosinski, J. 1986 A survey of recent studies on flame extinction. Prog. Energy Combust. Sci. 12 (2), 81–116.Google Scholar
Jiménez, C., Fernández-Galisteo, D. & Kurdyumov, V. N. 2015 DNS study of the propagation and flashback conditions of lean hydrogen–air flames in narrow channels: symmetric and non-symmetric solutions. Int. J. Hydrogen Energy 40 (36), 12541–12549.Google Scholar
Ju, Y. & Choi, C. W. 2003 An analysis of sub-limit flame dynamics using opposite propagating flames in mesoscale channels. Combust. Flame 133 (4), 483–493.Google Scholar
Ju, Y. & Maruta, K. 2011 Microscale combustion: technology development and fundamental research. Prog. Energy Combust. Sci. 37 (6), 669–715.Google Scholar
Ju, Y. & Xu, B. 2005 Theoretical and experimental studies on mesoscale flame propagation and extinction. Proc. Combust. Inst. 30 (2), 2445–2453.Google Scholar
Ju, Y. & Xu, B. 2006 Studies of the effects of radical quenching and flame stretch on mesoscale combustion. In 44th AIAA Aerospace Sciences Meeting and Exhibit, p. 1351. AIAA.Google Scholar
Kagan, L. & Sivashinsky, G. 2010 On the transition from deflagration to detonation in narrow tubes. Flow Turbul. Combust. 84 (3), 423–437.Google Scholar
Kaisare, N. S. & Vlachos, D. G. 2012 A review on microcombustion: fundamentals, devices and applications. Prog. Energy Combust. Sci. 38 (3), 321–359.Google Scholar
Karlovitz, B., Denniston, D. W., Knapschaefer, D. H. & Wells, F. E. 1953 Flame propagation across velocity gradients. In 4th Symposium (Intl.) on Combustion, pp. 613–620. The Combustion Institute.Google Scholar
Kazakov, K. A. 2012 Analytical study in the mechanism of flame movement in horizontal tubes. Phys. Fluids 24 (2), 022108.Google Scholar
Kee, R. J., Rupley, F. M. & Miller, J. A.1989 Chemkin-II: a fortran chemical kinetics package for the analysis of gas-phase chemical kinetics. Tech. Rep. Sandia National Labs., Livermore, CA (USA).Google Scholar
Kim, N. I., Aizumi, S., Yokomori, T., Kato, S., Fujimori, T. & Maruta, K. 2007 Development and scale effects of small swiss-roll combustors. Proc. Combust. Inst. 31 (2), 3243–3250.Google Scholar
Kim, N. I., Kataoka, T., Maruyama, S. & Maruta, K. 2005 Flammability limits of stationary flames in tubes at low pressure. Combust. Flame 141 (1), 78–88.Google Scholar
Kim, N. I. & Maruta, K. 2006 A numerical study on propagation of premixed flames in small tubes. Combust. Flame 146 (1), 283–301.Google Scholar
Kizaki, Y., Nakamura, H., Tezuka, T., Hasegawa, S. & Maruta, K. 2015 Effect of radical quenching on ch 4/air flames in a micro flow reactor with a controlled temperature profile. Proc. Combust. Inst. 35 (3), 3389–3396.Google Scholar
Koren, C.2016 Modélisation des transferts de chaleur couplés pour la simulation multi-physique des chambres de combustion. PhD thesis, Université Paris-Saclay.Google Scholar
Kuo, C. H. & Ronney, P. D. 2007 Numerical modeling of non-adiabatic heat-recirculating combustors. Proc. Combust. Inst. 31 (2), 3277–3284.Google Scholar
Kurdyumov, V. N. 2011 Lewis number effect on the propagation of premixed flames in narrow adiabatic channels: symmetric and non-symmetric flames and their linear stability analysis. Combust. Flame 158 (7), 1307–1317.Google Scholar
Kurdyumov, V. N. & Fernandez-Tarrazo, E. 2002 Lewis number effect on the propagation of premixed laminar flames in narrow open ducts. Combust. Flame 128 (4), 382–394.Google Scholar
Kurdyumov, V. N. & Jiménez, C. 2014 Propagation of symmetric and non-symmetric premixed flames in narrow channels: influence of conductive heat-losses. Combust. Flame 161 (4), 927–936.Google Scholar
Lewis, B. & Von Elbe, G. 1987 Combustion, Flames and Explosions of Gases. Elsevier.Google Scholar
Li, J., Chou, S. K., Yang, W. M. & Li, Z. W. 2009 A numerical study on premixed micro-combustion of ch 4–air mixture: effects of combustor size, geometry and boundary conditions on flame temperature. Chem. Engng J. 150 (1), 213–222.Google Scholar
Lodato, G., Vervisch, L. & Domingo, P. 2009 A compresssible wall-adapting similarity mixed model for large-eddy simulation of the impinging round jet. Phys. Fluids 21, 035102.Google Scholar
Lodier, G., Merlin, C., Domingo, P., Vervisch, L. & Ravet, F. 2012 Self-ignition scenarios after rapid compression of a turbulent mixture weakly-stratified in temperature. Combust. Flame 159 (11), 3358–3371.Google Scholar
Maruta, K., Kataoka, T., Kim, N. I., Minaev, S. & Fursenko, R. 2005 Characteristics of combustion in a narrow channel with a temperature gradient. Proc. Combust. Inst. 30 (2), 2429–2436.Google Scholar
Merlin, C., Domingo, P. & Vervisch, L. 2013 Immersed boundaries in large eddy simulation of compressible flows. Flow Turbul. Combust. 90 (1), 29–68.Google Scholar
Michaelis, B. & Rogg, B. 2004 FEM-simulation of laminar flame propagation. I: two-dimensional flames. J. Comput. Phys. 196 (2), 417–447.Google Scholar
Miesse, C. M., Masel, R. I., Jensen, C. D., Shannon, M. A. & Short, M. 2004 Submillimeter-scale combustion. AIChE J. 50 (12), 3206–3214.Google Scholar
MomentivePerformance Materials Inc. 2017 Thermal properties of fused quartz. Tech. Rep. https://www.momentive.com/en-US/categories/quartz/thermal-properties/.Google Scholar
Nakamura, H., Fan, A., Minaev, S., Sereshchenko, E., Fursenko, R., Tsuboi, Y. & Maruta, K. 2012 Bifurcations and negative propagation speeds of methane/air premixed flames with repetitive extinction and ignition in a heated microchannel. Combust. Flame 159 (4), 1631–1643.Google Scholar
Norton, D. G. & Vlachos, D. G. 2003 Combustion characteristics and flame stability at the microscale: a CFD study of premixed methane/air mixtures. Chem. Engng Sci. 58 (21), 4871–4882.Google Scholar
Petit, X., Ribert, G., Lartigue, G. & Domingo, P. 2013 Large-eddy simulation of supercritical fluid injection. J. Supercritical Fluids 84, 61–73.Google Scholar
Pizza, G., Frouzakis, C. E., Mantzaras, J., Tomboulides, A. G. & Boulouchos, K. 2010 Three-dimensional simulations of premixed hydrogen/air flames in microtubes. J. Fluid Mech. 658, 463–491.Google Scholar
Poinsot, T. J., Haworth, D. C. & Bruneaux, G. 1993 Direct simulation and modeling of flame-wall interaction for premixed turbulent combustion. Combust. Flame 95 (1–2), 118–132.Google Scholar
Poinsot, T. J. & Lele, S. K. 1992 Boundary conditions for direct simulations of compressible viscous flows. J. Comput. Phys. 101 (1), 104–129.Google Scholar
Richecoeur, F. & Kyritsis, D. C. 2005 Experimental study of flame stabilization in low reynolds and dean number flows in curved mesoscale ducts. Proc. Combust. Inst. 30 (2), 2419–2427.Google Scholar
Ronney, P. D. 2003 Analysis of non-adiabatic heat-recirculating combustors. Combust. Flame 135 (4), 421–439.Google Scholar
Ruetsch, G. R., Vervisch, L. & Liñán, A. 1995 Effects of heat release on triple flame. Phys. Fluids 7 (6), 1447–1454.Google Scholar
Sánchez-Sanz, M., Fernández-Galisteo, D. & Kurdyumov, V. 2014 Effect of the equivalence ratio, Damköhler number, Lewis number and heat release on the stability of laminar premixed flames in microchannels. Combust. Flame 161 (5), 1282–1293.Google Scholar
Short, M. & Kessler, D. A. 2009 Asymptotic and numerical study of variable-density premixed flame propagation in a narrow channel. J. Fluid Mech. 638, 305–337.Google Scholar
Smith, G. P., Golden, D. M., Frenklach, M., Moriarty, N. W., Eiteneer, B., Goldenberg, M., Bowman, C. T., Hanson, R. K., Song, S., Gardiner, W. C., Lissianski, V. V. & Qin, Z.1999 Tech. Rep. http://www.me.berkeley.edu/gri-mech/.Google Scholar
Smooke, M. D. & Giovangigli, V. 1991 Formulation of the premixed and nonpremixed test problems. In Reduced Kinetic Mechanisms and Asymptotic Approximations for Methane–Air Flames, pp. 1–28. Springer.Google Scholar
Srinivasan, R., Hsing, I., Berger, P. E., Jensen, K. F., Firebaugh, S. L., Schmidt, M. A., Harold, M. P., Lerou, J. J. & Ryley, J. F. 1997 Micromachined reactors for catalytic partial oxidation reactions. AIChE J. 43 (11), 3059–3069.Google Scholar
Subramanian, V., Domingo, P. & Vervisch, L. 2010 Large-eddy simulation of forced ignition of an annular bluff-body burner. Combust. Flame 157 (3), 579–601.Google Scholar
Swanson, R. & Turkel, E. 1992 On central-difference and upwind schemes. J. Comput. Phys. 101 (2), 292–306.Google Scholar
Tatsumi, S., Martinelli, L. & Jameson, A. 1995 Flux-limited schemes for the compressible Navier–Stokes equations. AIAA J. 33 (2), 252–261.Google Scholar
Tsai, C. H. 2008 The asymmetric behavior of steady laminar flame propagation in ducts. Combust. Sci. Tech. 180 (3), 533–545.Google Scholar
Veeraragavan, A. & Cadou, C. P. 2011 Flame speed predictions in planar micro/mesoscale combustors with conjugate heat transfer. Combust. Flame 158 (11), 2178–2187.Google Scholar
Vican, J., Gajdeczko, B. F., Dryer, F. L., Milius, D. L., Aksay, I. A. & Yetter, R. A. 2002 Development of a microreactor as a thermal source for microelectromechanical systems power generation. Proc. Combust. Inst. 29 (1), 909–916.Google Scholar
Walther, D. C. & Ahn, J. 2011 Advances and challenges in the development of power-generation systems at small scales. Prog. Energy Combust. Sci. 37 (5), 583–610.Google Scholar
Weinberg, F. J., Rowe, D. M., Min, G. & Ronney, P. D. 2002 On thermoelectric power conversion from heat recirculating combustion systems. Proc. Combust. Inst. 29 (1), 941–947.Google Scholar
Xie, Z., Yang, Z., Zhang, L. & Liu, C. 2015 Effects of non-catalytic surface reactions on the ch 4–air premixed flame within micro-channels. RSC Adv. 5 (43), 34272–34280.Google Scholar
Xu, B. & Ju, Y. 2007 Experimental study of spinning combustion in a mesoscale divergent channel. Proc. Combust. Inst. 31 (2), 3285–3292.Google Scholar
Yetter, R. A., Yang, V., Wu, M. H., Wang, Y., Milius, D., Aksay, I. A. & Dryer, F. L. 2007 Combustion issues and approaches for chemical microthrusters. Intl J. Energy Mat. Chem. Prop. 6 (4), 394–424.Google Scholar