Published online by Cambridge University Press: 06 November 2023
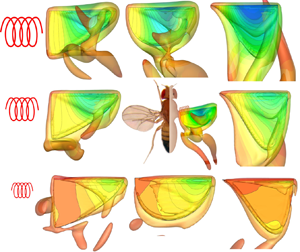
The power exchange between fluid and structure plays a significant role in the force production and flight efficiency of flapping wings in insects and artificial flyers. This work numerically investigates the performance of flapping wings by using a high-fidelity fluid–structure interaction solver. Simulations are conducted by varying the hinge flexibility (measured by the Cauchy number,  $Ch$, i.e. the ratio between aerodynamic and torsional elastic forces) and the wing shape (quantified by the radius of the first moment of area,
$Ch$, i.e. the ratio between aerodynamic and torsional elastic forces) and the wing shape (quantified by the radius of the first moment of area,  $\bar {r}_1$). Results show that the lift production is optimal at
$\bar {r}_1$). Results show that the lift production is optimal at  $0.05 < Ch \leq 0.2$ and larger
$0.05 < Ch \leq 0.2$ and larger  $\bar {r}_1$ where the minimum angle of attack is around
$\bar {r}_1$ where the minimum angle of attack is around  $45^\circ$ at midstroke. The power economy is maximised for wings with lower
$45^\circ$ at midstroke. The power economy is maximised for wings with lower  $\bar {r}_1$ near
$\bar {r}_1$ near  $Ch=0.2$. Power analysis indicates that the optimal performance measured by the power economy is obtained for those cases where two important power synchronisations occur: anti-synchronisation of the pitching elastic power and the pitching aerodynamic and inertial powers and nearly in-phase synchronisation of the flapping aerodynamic power and the total input power of the system. While analysis of the kinematics for the different wing shapes and hinge stiffnesses reveals that the optimal performance occurs when the timing of pitch and stroke reversals are matched, thus supporting the effective transfer of input power from flapping to passive pitching and into the fluid. These results suggest that careful optimisation between wing shapes and hinge properties can allow insects and robots to exploit the passive dynamics to improve flight performance.
$Ch=0.2$. Power analysis indicates that the optimal performance measured by the power economy is obtained for those cases where two important power synchronisations occur: anti-synchronisation of the pitching elastic power and the pitching aerodynamic and inertial powers and nearly in-phase synchronisation of the flapping aerodynamic power and the total input power of the system. While analysis of the kinematics for the different wing shapes and hinge stiffnesses reveals that the optimal performance occurs when the timing of pitch and stroke reversals are matched, thus supporting the effective transfer of input power from flapping to passive pitching and into the fluid. These results suggest that careful optimisation between wing shapes and hinge properties can allow insects and robots to exploit the passive dynamics to improve flight performance.