1 Introduction
In a homogeneous medium where dispersed clusters of a second phase exist in a saturated solution, Ostwald ripening is the mechanism by which the larger clusters grow at the expense of the smaller ones. The mechanism is well understood both in solids, e.g. for crystallization of rocks, and in bulk (or free) liquid solutions (Epstein & Plesset Reference Epstein and Plesset1950; Greenwood Reference Greenwood1956; Lifshitz & Slyozov Reference Lifshitz and Slyozov1961; Voorhees Reference Voorhees1985; Schmelzer & Schweitzer Reference Schmelzer and Schweitzer1987) and is driven by capillary pressure differences that cause inter-cluster diffusion through a saturated solution. In the case of a solid porous matrix filled with an immobile saturated solution however, the evolution of clusters of a second phase is much more difficult to predict. Pore-scale capillary pressure, the difference between the wetting and non-wetting phase pressures on both sides of an interface, remains linked to the shape of the clusters by Laplace’s law along the unsupported interfaces between the two phases, but is now determined by the geometry of the pore space (Bear Reference Bear1972), which can be extremely complex in real rocks, as shown by recent advances in microtomography imaging (Blunt et al.
Reference Blunt, Bijeljic, Dong, Gharbi, Iglauer, Mostaghimi, Paluszny and Pentland2013; Cnudde & Boone Reference Cnudde and Boone2013; Schlüter et al.
Reference Schlüter, Sheppard, Brown and Wildenschild2014). In this paper we specifically explore the impact of pore structure on Ostwald ripening in a supercritical
![]() $\text{CO}_{2}$
-water system.
$\text{CO}_{2}$
-water system.
An application of particular interest to the authors is that of residual trapping in the context of carbon capture and storage (Bachu Reference Bachu2008; Benson & Cole Reference Benson and Cole2008). Previous studies (Iglauer et al.
Reference Iglauer, Paluszny, Pentland and Blunt2011; Tanino & Blunt Reference Tanino and Blunt2012; Chaudhary et al.
Reference Chaudhary, Bayani Cardenas, Wolfe, Maisano, Ketcham and Bennett2013; Georgiadis et al.
Reference Georgiadis, Berg, Makurat, Maitland and Ott2013; Andrew, Bijeljic & Blunt Reference Andrew, Bijeljic and Blunt2014b
; Geistlinger et al.
Reference Geistlinger, Mohammadian, Schlueter and Vogel2014; Rahman et al.
Reference Rahman, Lebedev, Barifcani and Iglauer2016) established that
![]() $\text{CO}_{2}$
can be locally trapped in the pore space by the residual trapping mechanism and that the trapped
$\text{CO}_{2}$
can be locally trapped in the pore space by the residual trapping mechanism and that the trapped
![]() $\text{CO}_{2}$
phase takes the form of disconnected ganglia with irregular shapes and varying sizes that can occupy one or multiple pores, as evidenced by microtomography imaging (a visualization of trapped fluids in a rock is shown in figure 1
a). In particular the authors reported power-law correlations for
$\text{CO}_{2}$
phase takes the form of disconnected ganglia with irregular shapes and varying sizes that can occupy one or multiple pores, as evidenced by microtomography imaging (a visualization of trapped fluids in a rock is shown in figure 1
a). In particular the authors reported power-law correlations for
![]() $\text{CO}_{2}$
cluster size distributions showing that a large number of very small clusters are observed and only few large clusters, although the large clusters represent the bulk of the phase volume. Since pore-scale capillary pressure gradients are the driver for the Ostwald ripening process, interfacial curvature measurements of residually trapped
$\text{CO}_{2}$
cluster size distributions showing that a large number of very small clusters are observed and only few large clusters, although the large clusters represent the bulk of the phase volume. Since pore-scale capillary pressure gradients are the driver for the Ostwald ripening process, interfacial curvature measurements of residually trapped
![]() $\text{CO}_{2}$
ganglia can be used to estimate the potential for the mechanism (Armstrong, Porter & Wildenschild Reference Armstrong, Porter and Wildenschild2012; Andrew, Bijeljic & Blunt Reference Andrew, Bijeljic and Blunt2014a
; Garing et al.
Reference Garing, de Chalendar, Voltolini, Ajo-Franklin and Benson2017a
). Garing et al. (Reference Garing, de Chalendar, Voltolini, Ajo-Franklin and Benson2017b
) conducted a
$\text{CO}_{2}$
ganglia can be used to estimate the potential for the mechanism (Armstrong, Porter & Wildenschild Reference Armstrong, Porter and Wildenschild2012; Andrew, Bijeljic & Blunt Reference Andrew, Bijeljic and Blunt2014a
; Garing et al.
Reference Garing, de Chalendar, Voltolini, Ajo-Franklin and Benson2017a
). Garing et al. (Reference Garing, de Chalendar, Voltolini, Ajo-Franklin and Benson2017b
) conducted a
![]() $\text{scCO}_{2}$
/brine drainage-imbibition experiment in a Boise sandstone (90 bars, 323 K) with repeated synchrotron-based X-ray microtomography imaging (
$\text{scCO}_{2}$
/brine drainage-imbibition experiment in a Boise sandstone (90 bars, 323 K) with repeated synchrotron-based X-ray microtomography imaging (
![]() $3.24~\unicode[STIX]{x03BC}\text{m}$
voxel size) over a period of 31 h after imbibition stops, in order to visualize and quantify the temporal evolution of residually trapped
$3.24~\unicode[STIX]{x03BC}\text{m}$
voxel size) over a period of 31 h after imbibition stops, in order to visualize and quantify the temporal evolution of residually trapped
![]() $\text{scCO}_{2}$
ganglia within the pore space of the imaged rock sample. The data suggest constant fluid displacement and fluid phase redistribution following the imbibition process caused by the interplay of different mechanisms, potentially including Ostwald ripening, as depicted in figure 1(b). Even more recently, Schlüter et al. (Reference Schlüter, Berg, Li, Vogel and Wildenschild2017) studied the pore-scale relaxation dynamics of fluid interfaces in a glass bead pack after a drainage process and also found that fluid phase redistribution continues long after the time at which equilibrium is typically declared in two-phase experiments for which a flux boundary condition is changed from flow to no flow.
$\text{scCO}_{2}$
ganglia within the pore space of the imaged rock sample. The data suggest constant fluid displacement and fluid phase redistribution following the imbibition process caused by the interplay of different mechanisms, potentially including Ostwald ripening, as depicted in figure 1(b). Even more recently, Schlüter et al. (Reference Schlüter, Berg, Li, Vogel and Wildenschild2017) studied the pore-scale relaxation dynamics of fluid interfaces in a glass bead pack after a drainage process and also found that fluid phase redistribution continues long after the time at which equilibrium is typically declared in two-phase experiments for which a flux boundary condition is changed from flow to no flow.
The aim of this paper is to provide the modelling tools to study the evolution of a system of ganglia governed by the ripening mechanism in order to determine the permanence of residual trapping. To simplify the problem, we specifically consider the case of residually trapped
![]() $\text{CO}_{2}$
ganglia that occupy one pore, as in figure 1(a), and explore the issue of whether stability is possible in such systems and the time scales over which these systems evolve.
$\text{CO}_{2}$
ganglia that occupy one pore, as in figure 1(a), and explore the issue of whether stability is possible in such systems and the time scales over which these systems evolve.

Figure 1. Visualization of trapped fluids in Boise sandstones. (a) Three-dimensional surface visualization of trapped wetting (blue) and non-wetting (red) phases in a Boise sandstone (data from the water–air gravity-driven imbibition experiments described in Garing et al. (Reference Garing, de Chalendar, Voltolini, Ajo-Franklin and Benson2017a
), sample is
![]() $530\times 515\times 255~\unicode[STIX]{x03BC}\text{m}$
). (b) Three-dimensional visualization of residual
$530\times 515\times 255~\unicode[STIX]{x03BC}\text{m}$
). (b) Three-dimensional visualization of residual
![]() $\text{scCO}_{2}$
ganglia (different disconnected ganglia are represented with different colours) trapped in a Boise sandstone after brine imbibition (data from the
$\text{scCO}_{2}$
ganglia (different disconnected ganglia are represented with different colours) trapped in a Boise sandstone after brine imbibition (data from the
![]() $\text{scCO}_{2}$
/brine imbibition experiment with time-lapse imaging after imbibition stops, as described in Garing et al.
Reference Garing, de Chalendar, Voltolini, Ajo-Franklin and Benson2017b
). The data illustrate the disappearance of a
$\text{scCO}_{2}$
/brine imbibition experiment with time-lapse imaging after imbibition stops, as described in Garing et al.
Reference Garing, de Chalendar, Voltolini, Ajo-Franklin and Benson2017b
). The data illustrate the disappearance of a
![]() $\text{scCO}_{2}$
bubble together with nearby
$\text{scCO}_{2}$
bubble together with nearby
![]() $\text{scCO}_{2}$
ganglia coalescence within a period of time of 7 h.
$\text{scCO}_{2}$
ganglia coalescence within a period of time of 7 h.
In the rare occasions where the Ostwald ripening mechanism is considered in porous media settings, other mechanisms like a constant pressure decline in the liquid play a disproportionate role (Li & Yortsos Reference Li and Yortsos1995; Dominguez, Bories & Prat Reference Dominguez, Bories and Prat2000), or cluster growth is strongly inhibited once there is significant interaction with the porous matrix walls (for viscous polymers and crystals growing in a solid matrix, e.g. in Schmelzer et al. Reference Schmelzer and Möller1995; Möller, Jacob & Schmelzer Reference Möller, Jacob and Schmelzer1998). Goldobin & Brilliantov (Reference Goldobin and Brilliantov2011) investigated the diffusion of gas in porous media using large-scale modelling of averaged thermodynamic properties, but did not model local geometry effects at the pore scale. Recent advances in pore-scale modelling (Meakin & Tartakovsky Reference Meakin and Tartakovsky2009; Blunt et al. Reference Blunt, Bijeljic, Dong, Gharbi, Iglauer, Mostaghimi, Paluszny and Pentland2013) provide tools to strengthen our understanding of single and multiphase flow, but they are less suited to the modelling of a phenomenon where the only transport mechanism is inter-cluster diffusion. A first class of tools discretizes the void space to compute flow and transport directly on a grid. Popular methods include particle-based methods (e.g. lattice Boltzmann (Chen & Doolen Reference Chen and Doolen1998; McClure et al. Reference McClure, Berrill, Gray and Miller2016a )); continuum methods that solve the Navier–Stokes equations using standard discretization schemes and different approaches to interface tracking (e.g. volume-of-fluid (Hirt & Nichols Reference Hirt and Nichols1981; Raeini, Blunt & Bijeljic Reference Raeini, Blunt and Bijeljic2012) or level set (Osher & Sethian Reference Osher and Sethian1988; Sussman, Smereka & Osher Reference Sussman, Smereka and Osher1994; Prodanović & Bryant Reference Prodanović and Bryant2006)); or more recently combinations of particle-based and continuum methods (e.g. McClure et al. Reference McClure, Berrill, Gray and Miller2016b ). However, one of the main drawbacks of grid-based higher fidelity simulations at very low capillary numbers is that spurious currents can make the simulations inconsistent and unphysical (in the case of volume-of-fluid methods), or that mass is not always rigorously conserved (in the case of level-set methods). Another common drawback of direct modelling approaches is their computational cost. This is in contrast to the large body of work on pore network modelling approaches in which the geometry of the pore space and physical processes are largely simplified (Fatt Reference Fatt1956; Dias & Payatakes Reference Dias and Payatakes1986a ; Pereira et al. Reference Pereira, Pinczewski, Chan, Paterson and Øren1996; Bakke & Øren Reference Bakke and Øren1997; Øren et al. Reference Øren, Bakke and Arntzen1998; Fischer & Celia Reference Fischer and Celia1999; Blunt Reference Blunt2001; Sok et al. Reference Sok, Knackstedt, Sheppard, Pinczewski, Lindquist, Venkatarangan and Paterson2002; Valvatne & Blunt Reference Valvatne and Blunt2003; Joekar-Niasar, Hassanizadeh & Leijnse Reference Joekar-Niasar, Hassanizadeh and Leijnse2008; Idowu & Blunt Reference Idowu and Blunt2010; Joekar-Niasar, Hassanizadeh & Dahle Reference Joekar-Niasar, Hassanizadeh and Dahle2010), which is why we choose this approach in the work presented here.
A key component of this approach is the generation of pore networks that are representative of real rocks, either directly from pore space images (e.g. by applying a thinning method to extract the skeleton or medial axis as in Lindquist et al. (Reference Lindquist, Lee, Coker, Jones and Spanne1996), or by using a maximal ball algorithm as in Silin & Patzek Reference Silin and Patzek2006), by process-based reconstruction (Øren & Bakke Reference Øren and Bakke2002) or by some method that uses random number generators to produce networks that are statistically representative of real rocks (Sok et al. Reference Sok, Knackstedt, Sheppard, Pinczewski, Lindquist, Venkatarangan and Paterson2002; Arns et al. Reference Arns, Robins, Sheppard, Sok, Pinczewski and Knackstedt2004). More recently, Idowu (Reference Idowu2009) built on Sok et al. (Reference Sok, Knackstedt, Sheppard, Pinczewski, Lindquist, Venkatarangan and Paterson2002) and Arns et al. (Reference Arns, Robins, Sheppard, Sok, Pinczewski and Knackstedt2004) to propose an algorithm that can generate a network of arbitrary size using as inputs pore body and throat size distributions and connectivity. In the appendix to this paper we present a technique that goes one step further in matching statistical properties extracted from real rocks. The algorithm we propose can be used to generate networks of arbitrary size, and matches target distributions for pore body and throat radius, for coordination number and for throat length. Body and throat radii and body radius and coordination number are also correlated using greedy heuristics (it would not be difficult to modify the algorithm to use additional information on these correlations if it were available). Ensuring the throat lengths are as realistic as possible is crucial in our application where diffusion paths have a high impact on evolution.
Pore-scale modelling approaches are usually designed to study situations where there is advective transport of a fluid, be it single or multiphase. For the Ostwald ripening mechanism, we model a situation where there is negligible advection (at most there are quasi-static displacements, as in Dias & Payatakes Reference Dias and Payatakes1986b
). Accordingly, Fickian diffusion of gas between the clusters is the only type of transport we consider, and we adapt the classical pore network modelling approach to our setting by tracking only the interfaces between the liquid and gas phases. The ripening mechanism can be decomposed into two processes operating on different time scales: the diffusion of solute gas through the liquid and the readjustment of the
![]() $\text{CO}_{2}$
-brine interfaces to accommodate changes in mass. In the geological storage setting, the diffusivity of
$\text{CO}_{2}$
-brine interfaces to accommodate changes in mass. In the geological storage setting, the diffusivity of
![]() $\text{CO}_{2}$
in brine is around
$\text{CO}_{2}$
in brine is around
![]() $3.64\times 10^{-9}~\text{m}^{2}~\text{s}^{-1}$
(Cadogan, Maitland & Trusler Reference Cadogan, Maitland and Trusler2014), to be compared to the product of the speed of sound in supercritical carbon dioxide with the typical length of a gas ganglion in porous media,
$3.64\times 10^{-9}~\text{m}^{2}~\text{s}^{-1}$
(Cadogan, Maitland & Trusler Reference Cadogan, Maitland and Trusler2014), to be compared to the product of the speed of sound in supercritical carbon dioxide with the typical length of a gas ganglion in porous media,
![]() ${\sim}300~\text{m}~\text{s}^{-1}\ast 100\times 10^{-6}~\text{m}=0.03~\text{m}^{2}~\text{s}^{-1}$
(Estrada-Alexanders & Trusler Reference Estrada-Alexanders and Trusler1998); and we will therefore assume that interface readjustment is instantaneous relative to the diffusive transport of solute
${\sim}300~\text{m}~\text{s}^{-1}\ast 100\times 10^{-6}~\text{m}=0.03~\text{m}^{2}~\text{s}^{-1}$
(Estrada-Alexanders & Trusler Reference Estrada-Alexanders and Trusler1998); and we will therefore assume that interface readjustment is instantaneous relative to the diffusive transport of solute
![]() $\text{CO}_{2}$
. This allows us to propose a simple sequential method to solving for evolution.
$\text{CO}_{2}$
. This allows us to propose a simple sequential method to solving for evolution.
To summarize, three main contributions are made in this paper: (i) a significant extension to the classic pore network modelling framework to allow key physical variables to vary continuously within the pore space, (ii) an algorithmic approach in pore network models to solving for evolution of capillary pressure dominated regimes where the driving force is inter-cluster diffusion and (iii) insights on the fundamental difference in the relationship between mass and capillary pressure of a gas cluster in the capillary tube and porous media settings. Additionally, we apply these methods to some realistic geometries to estimate the extent and the rate of ripening for a typical
![]() $\text{CO}_{2}$
storage scenario.
$\text{CO}_{2}$
storage scenario.
This work builds on the framework introduced in de Chalendar (Reference de Chalendar2016a ), de Chalendar, Garing & Benson (Reference de Chalendar, Garing and Benson2017).
2 Governing equations for Ostwald ripening
2.1 Comparison of the framework to previous work
As was mentioned in § 1, the Ostwald ripening problem has been extensively studied, in particular in the case of a free liquid solution. The problem we study here is quite different from the one that is typically studied, and consequently our approach is to capture individual bubble dynamics rather than the mean behaviour of a population of bubbles.
We highlight the foundational equations for the classical Ostwald ripening theories in appendix A. Previous work on the Ostwald ripening problem (Greenwood Reference Greenwood1956; Lifshitz & Slyozov Reference Lifshitz and Slyozov1961; Voorhees Reference Voorhees1985; Schmelzer & Schweitzer Reference Schmelzer and Schweitzer1987; Schmelzer et al. Reference Schmelzer and Möller1995) is commonly based on the Ostwald–Freundlich equation, itself based on a relation between a liquid and its vapour (Thomson Reference Thomson1872), and assumes the gas follows the ideal gas law.
A major breakthrough in the study of the Ostwald ripening phenomenon was the seminal paper by Lifschitz and Slyozov (Lifshitz & Slyozov Reference Lifshitz and Slyozov1961), who consider a slightly supersaturated solution, and were able to make quantitative predictions on the asymptotic behaviour of coarsening systems without explicitly solving the relevant equations. They consider diffusion currents of solute between the grains and the solution, and use a variation of the Ostwald–Freundlich equation (for concentration), Fick’s law for diffusion and conservation of mass (assuming that no new particles appear) to derive a governing equation for a particle radius distribution function. At long times, it is then shown that this equation simplifies to an ordinary differential equation, which can be solved to make predictions on the long-term evolution of the mean and critical radii. We note that the Lifschitz–Slyozov, or Lifschitz–Slyozov–Wagner (LSW) theory, like Greenwood (Reference Greenwood1956), considers that grains are far enough apart that a spherical diffusion regime can be considered, and establishes asymptotic results on the evolution of the radius distribution function. A review of this classical theory and of subsequent results is given in Voorhees (Reference Voorhees1985). Some attempts were later made to extend this theory to porous media, e.g. in Schmelzer et al. (Reference Schmelzer and Möller1995), which builds off the same equations as in the LSW theory but then assumes growth stops or is strongly inhibited as soon as the growing grains start interacting with the solid matrix.
In contrast, in this work we consider a solution of brine that is initially saturated with
![]() $\text{CO}_{2}$
. The
$\text{CO}_{2}$
. The
![]() $\text{CO}_{2}$
is supercritical in our conditions, so that the ideal gas law, and consequently the Ostwald–Freundlich equation, may not be used. Additionally, the gas ganglia are much closer then in the classic ripening theories (the distance between two ganglia is of the same order as the size of the ganglia), and diffusion paths are constrained by the morphology of the rock structure, so that a spherical diffusion regime may not be considered. The system is typically initialized such that the ganglia are already interacting with the solid matrix, as shown in the microtomography image in figure 1(a). As such, in our framework we only consider pairwise interactions between ganglia, and do not use the mean-field approximation that was popularized by the LSW theory when considering ripening.
$\text{CO}_{2}$
is supercritical in our conditions, so that the ideal gas law, and consequently the Ostwald–Freundlich equation, may not be used. Additionally, the gas ganglia are much closer then in the classic ripening theories (the distance between two ganglia is of the same order as the size of the ganglia), and diffusion paths are constrained by the morphology of the rock structure, so that a spherical diffusion regime may not be considered. The system is typically initialized such that the ganglia are already interacting with the solid matrix, as shown in the microtomography image in figure 1(a). As such, in our framework we only consider pairwise interactions between ganglia, and do not use the mean-field approximation that was popularized by the LSW theory when considering ripening.
In the remainder of this section, we derive the governing equations for the Ostwald ripening problem in our setting.
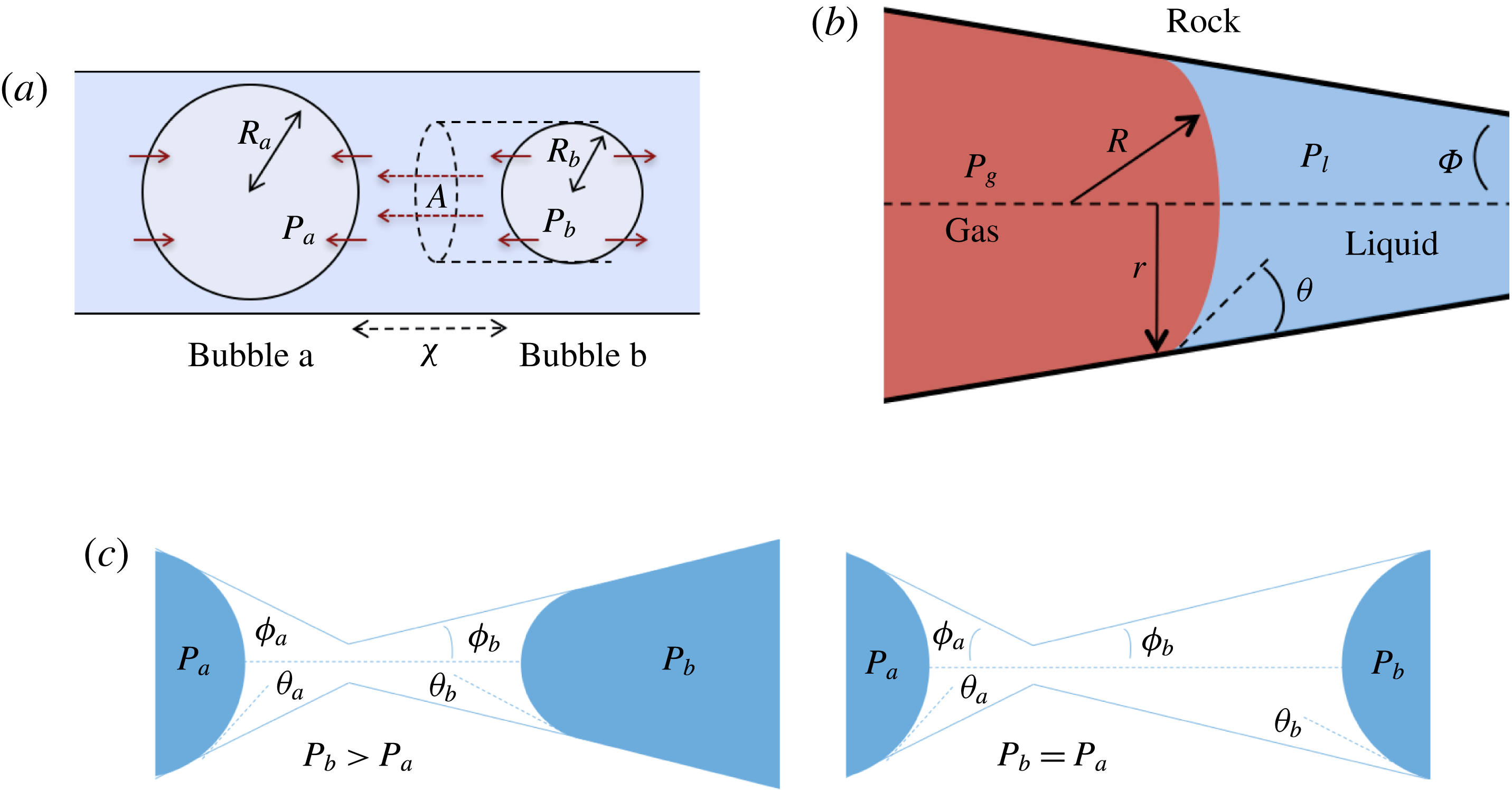
Figure 2. Comparing the capillary tube and porous media cases – figures 1 and 2 from de Chalendar et al. (Reference de Chalendar, Garing and Benson2017). (a) Idealized setting for Ostwald ripening in the capillary tube case. (b) Meniscus in a conical capillary (adapted from Dullien Reference Dullien2012, figure 2.11). (c) Simple two-bubble system in a porous medium, at disequilibrium and at equilibrium states.
2.2 Capillary tube case
We first consider the case of an initially saturated solution, where two spherical bubbles of gas – denoted by
![]() $a$
and
$a$
and
![]() $b$
in the following – appear at
$b$
in the following – appear at
![]() $t=0$
in a capillary tube, as shown in figure 2(a). The bubbles are constrained to be immobile, but mass can be transferred to the surrounding liquid by dissolution or exsolution. There is no interaction between the solid and the walls (the only role of the tube is to constrain diffusion paths to one-dimensional, rectilinear flow). We assume that the bubbles are at both mechanical and thermodynamic equilibrium with their immediate surroundings. We will refer to this setting as the capillary tube case. The ripening mechanism in this case is well described by three basic laws. Capillary pressure, or the difference in pressure between the gas and the liquid, is related to the shape of the interface by Laplace’s law, a statement of mechanical equilibrium of the gas bubble with the surrounding liquid:
$t=0$
in a capillary tube, as shown in figure 2(a). The bubbles are constrained to be immobile, but mass can be transferred to the surrounding liquid by dissolution or exsolution. There is no interaction between the solid and the walls (the only role of the tube is to constrain diffusion paths to one-dimensional, rectilinear flow). We assume that the bubbles are at both mechanical and thermodynamic equilibrium with their immediate surroundings. We will refer to this setting as the capillary tube case. The ripening mechanism in this case is well described by three basic laws. Capillary pressure, or the difference in pressure between the gas and the liquid, is related to the shape of the interface by Laplace’s law, a statement of mechanical equilibrium of the gas bubble with the surrounding liquid:
where
![]() $P_{a,b}$
is the pressure of the gas in bubble
$P_{a,b}$
is the pressure of the gas in bubble
![]() $a,b$
;
$a,b$
;
![]() $P_{l}$
is the pressure inside the liquid;
$P_{l}$
is the pressure inside the liquid;
![]() $\unicode[STIX]{x1D70E}$
is the interfacial tension and
$\unicode[STIX]{x1D70E}$
is the interfacial tension and
![]() $R_{a,b}$
is the radius of bubble
$R_{a,b}$
is the radius of bubble
![]() $a,b$
. We next consider that bubble
$a,b$
. We next consider that bubble
![]() $a,b$
is at local thermodynamic equilibrium with its immediate surroundings. Since the solute
$a,b$
is at local thermodynamic equilibrium with its immediate surroundings. Since the solute
![]() $\text{CO}_{2}$
is dilute in the brine (in the geological storage setting,
$\text{CO}_{2}$
is dilute in the brine (in the geological storage setting,
![]() $\text{CO}_{2}$
concentrations are not expected to rise above 5 % in mass (Kohl & Nielsen Reference Kohl and Nielsen1997)) we can apply Henry’s law, a first-order Taylor series expansion of the relation between pressure in the gas and concentration of solute in the liquid:
$\text{CO}_{2}$
concentrations are not expected to rise above 5 % in mass (Kohl & Nielsen Reference Kohl and Nielsen1997)) we can apply Henry’s law, a first-order Taylor series expansion of the relation between pressure in the gas and concentration of solute in the liquid:
where
![]() $C_{a,b}$
is the concentration of dissolved gas in the liquid at the interface between the liquid and bubble
$C_{a,b}$
is the concentration of dissolved gas in the liquid at the interface between the liquid and bubble
![]() $a,b$
and
$a,b$
and
![]() $H$
is Henry’s constant (we assume that we can use the same value of Henry’s constant for both bubbles). We can then use this to replace
$H$
is Henry’s constant (we assume that we can use the same value of Henry’s constant for both bubbles). We can then use this to replace
![]() $P_{a,b}$
in (2.1):
$P_{a,b}$
in (2.1):
With the concentrations in
![]() $\text{kg}~\text{m}^{-3}$
, we assume that the mass transfer rate of the dissolved gas in the liquid is governed to a first order by Fick’s law according to:
$\text{kg}~\text{m}^{-3}$
, we assume that the mass transfer rate of the dissolved gas in the liquid is governed to a first order by Fick’s law according to:
where
![]() $m_{a,b}$
is mass inside bubble
$m_{a,b}$
is mass inside bubble
![]() $a,b$
;
$a,b$
;
![]() $\unicode[STIX]{x0394}C_{a}=C_{b}-C_{a}=-\unicode[STIX]{x0394}C_{b}$
is the difference in concentration between bubbles
$\unicode[STIX]{x0394}C_{a}=C_{b}-C_{a}=-\unicode[STIX]{x0394}C_{b}$
is the difference in concentration between bubbles
![]() $a,b$
;
$a,b$
;
![]() $D$
is the diffusivity;
$D$
is the diffusivity;
![]() $A/x$
is the effective area-to-length ratio of the diffusion path between the two bubbles. We make the additional assumptions that the density
$A/x$
is the effective area-to-length ratio of the diffusion path between the two bubbles. We make the additional assumptions that the density
![]() $\unicode[STIX]{x1D70C}$
(for a
$\unicode[STIX]{x1D70C}$
(for a
![]() $1~\unicode[STIX]{x03BC}\text{m}$
bubble in a 15 MPa solution at 323 K, the change in density after considering capillary pressure is 0.2 % according to Linstrom & Mallard Reference Linstrom and Mallard2005) and temperature
$1~\unicode[STIX]{x03BC}\text{m}$
bubble in a 15 MPa solution at 323 K, the change in density after considering capillary pressure is 0.2 % according to Linstrom & Mallard Reference Linstrom and Mallard2005) and temperature
![]() $T$
of the gas are constant. In the capillary tube case, the bubbles are not in contact with the tube walls, so that we can also clearly relate the mass of a spherical bubble to its radius:
$T$
of the gas are constant. In the capillary tube case, the bubbles are not in contact with the tube walls, so that we can also clearly relate the mass of a spherical bubble to its radius:
Combining the equations above leads us to a coupled system of equations for the evolution of the radii
![]() $R_{a,b}$
:
$R_{a,b}$
:
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \frac{\unicode[STIX]{x2202}R_{a}}{\unicode[STIX]{x2202}t}=\frac{\unicode[STIX]{x1D6FC}}{R_{a}^{2}}\left(\frac{1}{R_{b}}-\frac{1}{R_{a}}\right),\\ \displaystyle \frac{\unicode[STIX]{x2202}R_{b}}{\unicode[STIX]{x2202}t}=\frac{\unicode[STIX]{x1D6FC}}{R_{b}^{2}}\left(\frac{1}{R_{a}}-\frac{1}{R_{b}}\right),\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \frac{\unicode[STIX]{x2202}R_{a}}{\unicode[STIX]{x2202}t}=\frac{\unicode[STIX]{x1D6FC}}{R_{a}^{2}}\left(\frac{1}{R_{b}}-\frac{1}{R_{a}}\right),\\ \displaystyle \frac{\unicode[STIX]{x2202}R_{b}}{\unicode[STIX]{x2202}t}=\frac{\unicode[STIX]{x1D6FC}}{R_{b}^{2}}\left(\frac{1}{R_{a}}-\frac{1}{R_{b}}\right),\end{array}\right\}\end{eqnarray}$$
where we introduced the coefficient
Note that
![]() $\unicode[STIX]{x1D6FC}$
depends on time through the effective area-to-length ratio for diffusion
$\unicode[STIX]{x1D6FC}$
depends on time through the effective area-to-length ratio for diffusion
![]() $(A/x)(t)$
. This coupled system of equations shows that a two-bubble system is thermodynamically unstable, and that a key driver for the ripening mechanism is the difference in partial pressures, or equivalently capillary pressures (since the pressure in the brine is assumed to be uniform), of the two gas bubbles. Even a slight difference in the interface radii can only amplify in time until the smaller radius goes to zero. A multi-bubble situation is unstable because a decrease in mass leads to an increase in capillary pressure which only reinforces the capillary pressure gradient. The system can be made dimensionless by introducing the initial mean radius
$(A/x)(t)$
. This coupled system of equations shows that a two-bubble system is thermodynamically unstable, and that a key driver for the ripening mechanism is the difference in partial pressures, or equivalently capillary pressures (since the pressure in the brine is assumed to be uniform), of the two gas bubbles. Even a slight difference in the interface radii can only amplify in time until the smaller radius goes to zero. A multi-bubble situation is unstable because a decrease in mass leads to an increase in capillary pressure which only reinforces the capillary pressure gradient. The system can be made dimensionless by introducing the initial mean radius
![]() $\bar{R}_{0}$
and dimensionless radii
$\bar{R}_{0}$
and dimensionless radii
![]() $R_{a,b}^{\ast }=R_{a,b}/\bar{R}_{0}$
:
$R_{a,b}^{\ast }=R_{a,b}/\bar{R}_{0}$
:
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \frac{\unicode[STIX]{x2202}R_{a}^{\ast }}{\unicode[STIX]{x2202}t}=\frac{\unicode[STIX]{x1D706}}{(R_{a}^{\ast })^{2}}\left(\frac{1}{R_{b}^{\ast }}-\frac{1}{R_{a}^{\ast }}\right),\\ \displaystyle \frac{\unicode[STIX]{x2202}R_{b}^{\ast }}{\unicode[STIX]{x2202}t}=\frac{\unicode[STIX]{x1D706}}{(R_{b}^{\ast })^{2}}\left(\frac{1}{R_{a}^{\ast }}-\frac{1}{R_{b}^{\ast }}\right),\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \frac{\unicode[STIX]{x2202}R_{a}^{\ast }}{\unicode[STIX]{x2202}t}=\frac{\unicode[STIX]{x1D706}}{(R_{a}^{\ast })^{2}}\left(\frac{1}{R_{b}^{\ast }}-\frac{1}{R_{a}^{\ast }}\right),\\ \displaystyle \frac{\unicode[STIX]{x2202}R_{b}^{\ast }}{\unicode[STIX]{x2202}t}=\frac{\unicode[STIX]{x1D706}}{(R_{b}^{\ast })^{2}}\left(\frac{1}{R_{a}^{\ast }}-\frac{1}{R_{b}^{\ast }}\right),\end{array}\right\}\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D706}$
has the dimension of a frequency:
$\unicode[STIX]{x1D706}$
has the dimension of a frequency:
The first term (
![]() $DA/x$
) is a characteristic flow rate for the diffusion process. The second one is characteristic of the dissolution process, since
$DA/x$
) is a characteristic flow rate for the diffusion process. The second one is characteristic of the dissolution process, since
![]() $\unicode[STIX]{x1D70E}/\bar{R}_{0}$
scales with the pressure exercised by capillary forces on a gas sphere of radius
$\unicode[STIX]{x1D70E}/\bar{R}_{0}$
scales with the pressure exercised by capillary forces on a gas sphere of radius
![]() $\bar{R}_{0}$
, so that
$\bar{R}_{0}$
, so that
![]() $\unicode[STIX]{x1D70E}/H\bar{R}_{0}$
scales with the concentration of
$\unicode[STIX]{x1D70E}/H\bar{R}_{0}$
scales with the concentration of
![]() $\text{CO}_{2}$
in the brine at equilibrium; and
$\text{CO}_{2}$
in the brine at equilibrium; and
![]() $\unicode[STIX]{x1D70C}\bar{R}_{0}^{3}$
is the mass in a sphere of radius
$\unicode[STIX]{x1D70C}\bar{R}_{0}^{3}$
is the mass in a sphere of radius
![]() $\bar{R}_{0}$
.
$\bar{R}_{0}$
.
We must now choose how to estimate the effective area-to-length ratio for Fickian diffusion
![]() $A/x$
. Unlike in most previous work on Ostwald ripening (see appendix A), we choose not to use a spherical regime for the diffusion process, because (i) we are ultimately trying to model a porous media situation as in figure 2 where the solid matrix constrains diffusion paths, and (ii) we cannot ignore the interactions between the ganglia since in our application the distance between the ganglia is of the same order as their size. Consequently, we choose the ratio of the projection of the smaller bubble on the larger one to the distance between the two bubbles as the area-to-length ratio, as shown in figure 2(a).
$A/x$
. Unlike in most previous work on Ostwald ripening (see appendix A), we choose not to use a spherical regime for the diffusion process, because (i) we are ultimately trying to model a porous media situation as in figure 2 where the solid matrix constrains diffusion paths, and (ii) we cannot ignore the interactions between the ganglia since in our application the distance between the ganglia is of the same order as their size. Consequently, we choose the ratio of the projection of the smaller bubble on the larger one to the distance between the two bubbles as the area-to-length ratio, as shown in figure 2(a).
So far we have considered only two bubbles of gas. In the remainder of this paper, we will assume that we can superpose pairwise interactions between multiple ganglia and extend the capillary tube approach to describe the ripening mechanism in porous media, as described in the following section.
2.3 Porous medium case
In the porous medium case, we again assume there is local mechanical and thermodynamic equilibrium near each gas ganglion, so we can apply Laplace’s and Henry’s laws, and that the diffusion process is well described by Fick’s law along tubes of uniform cross-sectional area between the ganglia. The only modification will be to the relation between interface radius and capillary pressure, to account for the interaction with the solid matrix, so when they interact with the solid, the ganglia may no longer be spherical. We assume that the solid matrix can locally be approximated as a conical frustum as shown in figure 2(b), so that Laplace’s law and geometric considerations can be used to derive the following relation:
where
![]() $\unicode[STIX]{x1D703}$
is the contact angle and
$\unicode[STIX]{x1D703}$
is the contact angle and
![]() $\unicode[STIX]{x1D719}$
is the angle at the summit of the cone. Figure 2(c) provides an idealized representation of gas ganglia in a porous medium. In the disequilibrium situation on the left, the curvatures and hence capillary pressures are different, whereas they are equal on the right. The equilibrium situation on the right is stable since a perturbation to the system will cause mass transfers that will bring it back to the configuration where the curvature of the two ganglia is the same.
$\unicode[STIX]{x1D719}$
is the angle at the summit of the cone. Figure 2(c) provides an idealized representation of gas ganglia in a porous medium. In the disequilibrium situation on the left, the curvatures and hence capillary pressures are different, whereas they are equal on the right. The equilibrium situation on the right is stable since a perturbation to the system will cause mass transfers that will bring it back to the configuration where the curvature of the two ganglia is the same.
In § 3, we describe how we represent the pore space using continuous pore network models. In § 4 we derive an algorithmic framework and detail how it is implemented in this study.

Figure 3. Two-dimensional representation of a simplistic continuous pore network model. The different colours for pore number 1 correspond to the different cases for the solution to the internal equilibrium problem in § 4.2: the ganglion is spherical and does not interact with the walls in the green zone, starts to protrude into the throat and interact with the porous matrix in the grey zone, and has invaded the throat in the orange zone.
3 Representation of continuous pore network models
3.1 Motivation
As in classic pore network modelling, we choose to represent the pore space using pore bodies which describe the larger voids in the rock and are connected by narrower pathways called throats. The pore space is represented as an undirected graph whose vertices are bodies and edges are throats. In classical pore network modelling however, physical variables such as pressure are usually assumed to be uniform within a throat or a body. A situation like the one in figure 2 where the capillary pressure varies continuously cannot be captured, which is why the traditional pore network modelling framework must be extended in this work. Key physical variables are allowed to vary continuously within the pore space, and throats are relaxed from cylindrical tubes to tubes that are the unions of conical frustums as shown in figure 3. This allows for a precise description of the location and shape of gas–liquid interfaces, which is necessary to correctly model the Ostwald ripening mechanism. Additionally an algorithm to generate pore network models that are statistically representative of the geometry of real rocks was developed and is described in appendix B. This algorithm can stochastically generate networks of arbitrary size whose statistical properties (body radius, throat radius, throat length, coordination number) match those of a real rock.
3.2 Elements of the pore space
3.2.1 Bodies
The nodes of the graph are what we call pore bodies. A pore body is assumed to be spherical and each body has a position and a radius. The choice of a sphere to represent pore bodies is guided by the physical process we are modelling: in the absence of interactions with the walls, the shape of a gas cluster will be spherical. In other words, the pore bodies that are represented in this manner are not necessarily spherical, but the radius we are assigning to each body is really the radius of the largest spherical bubble that could fit in that pore as described in the maximal ball algorithm (Silin & Patzek Reference Silin and Patzek2006).
3.2.2 Throats
The edges of the network are what we call throats. A pore throat represents a connection between two bodies. Pore throats are assigned a radius and a position that correspond to the position and radius of the constriction that defines the throat. In the maximal inscribed spheres (MIS) representation of the pore space, the pore throat constrictions would correspond to local minima for the mapping from the position along the skeleton to the MIS radii. Throats take the shape of the union of two conical frustums whose radius at every point along the medial axis of the graph is determined by linearly interpolating between the throat constriction and the nearest body.
3.2.3 Gas clusters
The pore space will be occupied either by a wetting or a non-wetting phase. An accurate representation of the interface between the phases is crucial as the shape of the interfaces determines evolution. The bodies display a spherical symmetry, and the throats a cylindrical one. In both cases, the problem becomes one-dimensional, and the state at any point in time of a system of ganglia will entirely be defined by the positions of the different interfaces along the medial axis of the pore space. If an interface is in a throat, it will take the form of a spherical cap positioned orthogonally to the medial axis; if it is in a body, it will take the form of a sphere centred at the body centre.
4 Algorithmic treatment of the Ostwald ripening mechanism
4.1 Simulation framework
For the geometry defined in § 3.2, the Ostwald ripening problem becomes one-dimensional, since we have a spherical symmetry in the bodies and a cylindrical one in the throats. The physical laws that describe the system are those we presented in § 2: Laplace, Henry and Fick’s laws. We decouple the Ostwald ripening mechanism in two processes that operate on different time scales. The slower mechanism is the diffusion of solute gas between ganglia whose pressures are different. The faster mechanism is the one by which a change in mass in a gas cluster changes the shape of the ganglia to ensure pressure is uniform within the cluster.
Accordingly, as illustrated in figure 4, we use a sequential algorithm that decomposes these two mechanisms. At each time step, we first solve what we call an internal equilibrium problem for each ganglion. The pressure inside each ganglion is assumed to be uniform, so solving the internal equilibrium problem requires finding the position and shape of the ganglion such that the mean curvature along the unsupported interfaces is identical at every point. We then search in the pore space for the available diffusion paths between the ganglia. We make the additional assumption that the diffusion process can be represented by superposition in a set of diffusive transfers between pairs of ganglia along each diffusion path. This is justified by the small time steps used for the calculations and the low concentrations of
![]() $\text{CO}_{2}$
in brine that are expected in the geologic storage setting (below 5 % mass (Kohl & Nielsen Reference Kohl and Nielsen1997)). We consequently compute a mass-transfer rate along each diffusion path. For each time step, the mass transfer by diffusion is calculated by summing the contributions from all adjacent ganglia. At the end of the time step, the shape and the location of the interfaces of the ganglia are adjusted based on the new internal equilibrium pressure. The algorithm then moves to the next time step.
$\text{CO}_{2}$
in brine that are expected in the geologic storage setting (below 5 % mass (Kohl & Nielsen Reference Kohl and Nielsen1997)). We consequently compute a mass-transfer rate along each diffusion path. For each time step, the mass transfer by diffusion is calculated by summing the contributions from all adjacent ganglia. At the end of the time step, the shape and the location of the interfaces of the ganglia are adjusted based on the new internal equilibrium pressure. The algorithm then moves to the next time step.

Figure 4. Flow chart for the sequential simulation algorithm.
4.2 Internal equilibrium problem
4.2.1 Solution outline
We call internal equilibrium the mechanism by which a cluster of gas modifies its shape after a change in mass to ensure that the pressure within the gas phase is the same at every point. Since the pressure in the liquid is assumed to be spatially uniform, Laplace’s law links the pressure in the gas to the interface radius of the cluster surface. Given a relationship between mass and volume, (since we are in reservoir conditions, density dependence on temperature and pressure is small and we assume it is constant in the numerical applications here. In general this assumption could be relaxed) solving the internal equilibrium problem can be reformulated as finding the interface radius such that the cluster has a given volume. In the same way we define pressure for the entire gas phase, we must define an interface radius that is the same everywhere along the unsupported interfaces (where Laplace’s law holds).
To simplify the problem, we restrict ourselves to the setting where the cluster of gas can only span a single body and its neighbouring throats (that have the shape of converging conical frustums according to the geometry we defined in § 3.2). In the future, the approach can and should be expanded to include multi-pore body ganglia. If the volume of gas is smaller than the pore body volume, then the cluster has a spherical shape and we assume that the cluster centre coincides with the body centre. If the volume of gas is larger, then the cluster extends into the pore throats and interacts with the solid matrix: its interface with the liquid in the throats take the shape of spherical caps. The maximum volume of gas that can be accommodated by the pore body is determined by the largest interface radius that can exist in all the throats. At the transition between the body and the throats, there is a discontinuity in capillary pressure (or equivalently interface radius) since the definition of the interface radius is different with and without interaction with the solid matrix. The capillary entry pressure of each of the throats is also different.

Figure 5. Solving the internal equilibrium problem in a body with five connecting throats. In (a,b), the cluster is shown in blue, and its volume is the same (
![]() $V_{cl}=1.19\ast 10^{7}~\unicode[STIX]{x03BC}\text{m}^{3}$
). In (c), the red dots show the threshold volumes for different cases of the internal equilibrium problem described in § 4.2. The volumes to the left of the sharp increase in interface radius correspond to
$V_{cl}=1.19\ast 10^{7}~\unicode[STIX]{x03BC}\text{m}^{3}$
). In (c), the red dots show the threshold volumes for different cases of the internal equilibrium problem described in § 4.2. The volumes to the left of the sharp increase in interface radius correspond to
![]() $V_{cl}\in [0,(1-\unicode[STIX]{x1D716})V_{B}]$
, where the cluster is in the green zone in figure 3. In the zoomed portion of the plot, the sharp increase corresponds to
$V_{cl}\in [0,(1-\unicode[STIX]{x1D716})V_{B}]$
, where the cluster is in the green zone in figure 3. In the zoomed portion of the plot, the sharp increase corresponds to
![]() $V_{cl}\in [(1-\unicode[STIX]{x1D716})V_{B},V_{B}]$
, and the portion between the red dots to
$V_{cl}\in [(1-\unicode[STIX]{x1D716})V_{B},V_{B}]$
, and the portion between the red dots to
![]() $V_{cl}\in [V_{th}^{i},V_{th}^{i+1}]$
,
$V_{cl}\in [V_{th}^{i},V_{th}^{i+1}]$
,
![]() $i=1\ldots n-1$
. Some interfaces are in the orange zone in figure 3, and some are in the grey zone. The volumes to the right of the sharp increase correspond to
$i=1\ldots n-1$
. Some interfaces are in the orange zone in figure 3, and some are in the grey zone. The volumes to the right of the sharp increase correspond to
![]() $V_{cl}\in [V_{th}^{n},V_{B}^{max}]$
. All interfaces are in the orange zone in figure 3. (a) Gas cluster – not at internal equilibrium. (b) Gas cluster – at internal equilibrium. (c) Solution of the internal equilibrium problem for the full range of available volumes (plot of
$V_{cl}\in [V_{th}^{n},V_{B}^{max}]$
. All interfaces are in the orange zone in figure 3. (a) Gas cluster – not at internal equilibrium. (b) Gas cluster – at internal equilibrium. (c) Solution of the internal equilibrium problem for the full range of available volumes (plot of
![]() $R_{cl}=f(V_{cl})$
for
$R_{cl}=f(V_{cl})$
for
![]() $V_{cl}\in [0,V_{B}^{max}]$
).
$V_{cl}\in [0,V_{B}^{max}]$
).
Figure 5 illustrates the internal equilibrium problem for a pore body neighboured by five throats. A cluster whose interfaces have different curvatures and that is therefore not internally equilibrated is shown in figure 5(a), whereas figure 5(b) shows a cluster with the same volume, but now at internal equilibrium. This internal equilibrium results in a unique relationship between the interface radius and the volume of gas that can be accommodated that depends on the pore size and connected throats. The solution to the problem for the full range of available volumes is shown in figure 5(c). The discontinuity in interface radius (or equivalently capillary pressure) that is shown in the zoomed portion of figure 5(c) is due to the difference in the relationship between shape and capillary pressure when the gas phase interacts with the solid matrix and when it does not.
In the remainder of this section, we first introduce some notation, and then present a solution for the internal equilibrium problem over the whole range of available gas volumes. We will show that solving the internal equilibrium problem amounts to solving for the roots of a polynomial of degree at most three.
4.2.2 Notation
We consider a body neighboured by
![]() $n$
throats. We call
$n$
throats. We call
![]() $V_{cl}$
the volume of the gas cluster,
$V_{cl}$
the volume of the gas cluster,
![]() $V_{B}$
the volume of the body and
$V_{B}$
the volume of the body and
![]() $V_{B}^{max}$
the maximum volume of gas that can fit into the pore body and its neighbouring throats. (
$V_{B}^{max}$
the maximum volume of gas that can fit into the pore body and its neighbouring throats. (
![]() $V_{B}^{max}$
is defined by the throat constriction where the interface radius is largest.) In the remainder of the section, we will use a lowercase
$V_{B}^{max}$
is defined by the throat constriction where the interface radius is largest.) In the remainder of the section, we will use a lowercase
![]() $r$
to denote the radius of a geometric element of the pore space and an uppercase
$r$
to denote the radius of a geometric element of the pore space and an uppercase
![]() $R$
to denote the radius of a gas–liquid interface. In a conical frustum, these can be related using Laplace’s law and geometric considerations, as stated in (2.10) (see figure 2
b). We call
$R$
to denote the radius of a gas–liquid interface. In a conical frustum, these can be related using Laplace’s law and geometric considerations, as stated in (2.10) (see figure 2
b). We call
![]() $r_{th}^{i}$
,
$r_{th}^{i}$
,
![]() $i=1\ldots n$
the radii of the throats at the constriction and
$i=1\ldots n$
the radii of the throats at the constriction and
![]() $r_{b,th}^{i}$
,
$r_{b,th}^{i}$
,
![]() $i=1\ldots n$
the radii of the throats at the junction with the body. The throats are ordered such that
$i=1\ldots n$
the radii of the throats at the junction with the body. The throats are ordered such that
![]() $R_{b,th}^{1}>\cdots >R_{b,th}^{n}$
. We call
$R_{b,th}^{1}>\cdots >R_{b,th}^{n}$
. We call
![]() $V_{th}^{i}$
,
$V_{th}^{i}$
,
![]() $i=1\ldots n$
the threshold volume for throat
$i=1\ldots n$
the threshold volume for throat
![]() $i$
, defined as the volume of gas such that the cluster starts invading throat
$i$
, defined as the volume of gas such that the cluster starts invading throat
![]() $i$
. We call
$i$
. We call
![]() $V_{con}^{i}(R_{cl})$
,
$V_{con}^{i}(R_{cl})$
,
![]() $i=1\ldots n$
the volume of gas in the conical frustum when the interface radius is
$i=1\ldots n$
the volume of gas in the conical frustum when the interface radius is
![]() $R_{cl}$
. In the following, we give the form of the solution for the range of volumes where the gas (i) is a spherical bubble (
$R_{cl}$
. In the following, we give the form of the solution for the range of volumes where the gas (i) is a spherical bubble (
![]() $V_{cl}\in [0,(1-\unicode[STIX]{x1D716})V_{B}]$
); (ii) starts interacting with the solid matrix (
$V_{cl}\in [0,(1-\unicode[STIX]{x1D716})V_{B}]$
); (ii) starts interacting with the solid matrix (
![]() $V_{cl}\in [(1-\unicode[STIX]{x1D716})V_{B},V_{B}]$
; (iii) has penetrated some of the throats (
$V_{cl}\in [(1-\unicode[STIX]{x1D716})V_{B},V_{B}]$
; (iii) has penetrated some of the throats (
![]() $V_{cl}\in [V_{th}^{i},V_{th}^{i+1}]$
,
$V_{cl}\in [V_{th}^{i},V_{th}^{i+1}]$
,
![]() $i=1\ldots n-1$
) and (iv) has penetrated all of the throats (
$i=1\ldots n-1$
) and (iv) has penetrated all of the throats (
![]() $V_{cl}\in [V_{th}^{n},V_{B}^{max}]$
). The red markers in figure 5(c) show the transition from one volume interval to the next. (In our numerical applications we take
$V_{cl}\in [V_{th}^{n},V_{B}^{max}]$
). The red markers in figure 5(c) show the transition from one volume interval to the next. (In our numerical applications we take
![]() $\unicode[STIX]{x1D716}=0.01$
.)
$\unicode[STIX]{x1D716}=0.01$
.)
4.2.3 Solution for
 $V_{cl}\in [0,(1-\unicode[STIX]{x1D716})V_{B}]$
$V_{cl}\in [0,(1-\unicode[STIX]{x1D716})V_{B}]$
The solution for the internal equilibrium problem is trivial in this case, which corresponds to a ganglion in the green zone in figure 3. The cluster behaves as if it were in a bulk liquid and takes the shape of a spherical bubble so that:
4.2.4 Solution for
 $V_{cl}\in [(1-\unicode[STIX]{x1D716})V_{B},V_{B}]$
$V_{cl}\in [(1-\unicode[STIX]{x1D716})V_{B},V_{B}]$
In this volume interval we consider that the gas cluster starts to protrude into the largest pore throat and interact with the solid matrix, which corresponds to the case where part of the ganglion enters a zone like the one displayed in grey in figure 3. The capillary pressure defined by the radius of the body is higher than that defined by the lowest throat capillary entry pressure. (It can be proven that the statement is always true by using some simple trigonometry and the definitions of the interface radii in the capillary tube and porous media cases. In our setting, the radii of the body and throat constriction are given, and throat radius is assumed to vary linearly between the constriction and the body.) To numerically avoid computations with a discontinuity in the capillary pressure variable, we arbitrarily decide that the interface radius and gas cluster volume are linearly related in this (small) interval:
where the coefficients
![]() $A,B$
are defined by:
$A,B$
are defined by:
Given the coefficients
![]() $A,B$
, solving for
$A,B$
, solving for
![]() $R_{cl}$
is trivial.
$R_{cl}$
is trivial.
4.2.5 Solution for
 $V_{cl}\in [V_{th}^{i},V_{th}^{i+1}]$
,
$V_{cl}\in [V_{th}^{i},V_{th}^{i+1}]$
,
 $i=1\ldots n-1$
$i=1\ldots n-1$
In these volume intervals the cluster has penetrated some of the throats. Using the colours from figure 3, this corresponds to the case where the ganglion has reached the orange zone in some of its body’s adjacent throats and is in the grey zone for the other adjacent throats. The throats are ordered such that
![]() $R_{b,th}^{1}>\cdots >R_{b,th}^{n}$
(or equivalently, from lowest to highest capillary entry pressure). For
$R_{b,th}^{1}>\cdots >R_{b,th}^{n}$
(or equivalently, from lowest to highest capillary entry pressure). For
![]() $i=1\ldots n-1$
, if
$i=1\ldots n-1$
, if
![]() $V_{cl}\in [V_{th}^{i},V_{th}^{i+1}]$
, then throats
$V_{cl}\in [V_{th}^{i},V_{th}^{i+1}]$
, then throats
![]() $1\ldots i$
have been invaded by the cluster. The body is assumed to be entirely filled at this stage, so:
$1\ldots i$
have been invaded by the cluster. The body is assumed to be entirely filled at this stage, so:
where we defined the threshold volumes by
![]() $V_{th}^{1}=V_{B}$
and
$V_{th}^{1}=V_{B}$
and
As shown in appendix B, the volume of gas in the conical frustum that represents throat
![]() $i$
,
$i$
,
![]() $V_{con}^{i}$
, can be expressed as a cubic polynomial of the interface radius
$V_{con}^{i}$
, can be expressed as a cubic polynomial of the interface radius
![]() $R_{cl}$
and the expression is valid for
$R_{cl}$
and the expression is valid for
![]() $R_{cl}\in [R_{th}^{i},R_{b,th}^{i}]$
:
$R_{cl}\in [R_{th}^{i},R_{b,th}^{i}]$
:
 $$\begin{eqnarray}\displaystyle V_{con}^{i}(R_{cl}) & = & \displaystyle \frac{\unicode[STIX]{x03C0}}{3}\frac{h_{max}^{i}}{r_{th}^{i}-r_{b,th}^{i}}[R_{cl}\cos (\unicode[STIX]{x1D703}+\unicode[STIX]{x1D719}^{i})-r_{b,th}^{i}]\nonumber\\ \displaystyle & & \displaystyle \times \,[{r_{b,th}^{i}}^{2}+r_{b,th}^{i}R_{cl}\cos (\unicode[STIX]{x1D703}+\unicode[STIX]{x1D719}^{i})+(R_{cl}\cos (\unicode[STIX]{x1D703}+\unicode[STIX]{x1D719}^{i}))^{2}].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle V_{con}^{i}(R_{cl}) & = & \displaystyle \frac{\unicode[STIX]{x03C0}}{3}\frac{h_{max}^{i}}{r_{th}^{i}-r_{b,th}^{i}}[R_{cl}\cos (\unicode[STIX]{x1D703}+\unicode[STIX]{x1D719}^{i})-r_{b,th}^{i}]\nonumber\\ \displaystyle & & \displaystyle \times \,[{r_{b,th}^{i}}^{2}+r_{b,th}^{i}R_{cl}\cos (\unicode[STIX]{x1D703}+\unicode[STIX]{x1D719}^{i})+(R_{cl}\cos (\unicode[STIX]{x1D703}+\unicode[STIX]{x1D719}^{i}))^{2}].\end{eqnarray}$$
4.2.6 Solution for
 $V_{cl}\in [V_{th}^{n},V_{B}^{max}]$
$V_{cl}\in [V_{th}^{n},V_{B}^{max}]$
In this volume interval, all of the throats are invaded by the cluster, so they all contribute to total volume:
In figure 3, a cluster occupying body no. 1 has invaded both adjacent throats (zones in orange).
4.3 Diffusive transport
During the mass-transfer step, each cluster exchanges mass with the neighbouring gas clusters. We first search for the available diffusion paths between the clusters, and then compute the mass transferred along each path during a time step, as visualized on an example pore space in figure 6. A rectilinear diffusion regime is used.
4.3.1 Diffusion paths
Given a set of ganglia in the pore space, we must find all the available diffusion paths between them. There can be one, multiple or no diffusion path between two given clusters. We adapt the classic breadth-first search (Lee Reference Lee1961) to find all the diffusion paths between two nodes of the graph. As we search, we record the length of the path and the minimum area along the path, as these are the length and area available for diffusion. We also prevent the search algorithm from returning any cyclic paths (otherwise there could be an infinite number of diffusion paths returned by the algorithm). Diffusion paths are only calculated between bodies where gas is present, and do not continue along a trajectory after a ganglion is found. In other words, the presence of a ganglion is assumed to block diffusion from ‘downstream ganglia’. In this way, only a limited number of paths need to be considered.

Figure 6. Visualization of diffusion paths in an example pore space. Diffusion paths for the orange cluster are depicted in orange also.
4.3.2 Diffusive transport
We use the superposition approach that was introduced earlier to deal with computing mass-transfer rates for each ganglion. We consider a system with
![]() $n$
ganglia. When searching for diffusion paths in the previous step, ganglion
$n$
ganglia. When searching for diffusion paths in the previous step, ganglion
![]() $i$
was found to have
$i$
was found to have
![]() $k_{i}$
neighbours. For each neighbour
$k_{i}$
neighbours. For each neighbour
![]() $j$
,
$j$
,
![]() $j\in [1\ldots k_{i}]$
, the search algorithm recorded the minimum area along the diffusion path
$j\in [1\ldots k_{i}]$
, the search algorithm recorded the minimum area along the diffusion path
![]() $A_{ij}$
and the length of the diffusion path
$A_{ij}$
and the length of the diffusion path
![]() $x_{ij}$
. We can calculate the mass transferring from ganglion
$x_{ij}$
. We can calculate the mass transferring from ganglion
![]() $j$
to ganglion
$j$
to ganglion
![]() $i$
by using the interface radii of the two ganglia
$i$
by using the interface radii of the two ganglia
![]() $R_{i}$
and
$R_{i}$
and
![]() $R_{j}$
using an explicit time stepping procedure where
$R_{j}$
using an explicit time stepping procedure where
![]() $R_{i}$
and
$R_{i}$
and
![]() $R_{j}$
are evaluated at the beginning of the time step, as described in (2.1), (2.2) and (2.4):
$R_{j}$
are evaluated at the beginning of the time step, as described in (2.1), (2.2) and (2.4):
For each ganglion we sum the contributions from each path in which it appears, counting mass positively if it is flowing in the ganglion. This gives us the net mass influx
![]() $\unicode[STIX]{x2202}m_{i}/\unicode[STIX]{x2202}t$
to ganglion
$\unicode[STIX]{x2202}m_{i}/\unicode[STIX]{x2202}t$
to ganglion
![]() $i$
,
$i$
,
![]() $i\in [1\ldots n]$
:
$i\in [1\ldots n]$
:
We verify that mass is conserved at each time step by checking that the sum of all the net influxes is zero at every moment in time.
4.4 Time stepping
Some parts of the simulations require shorter time steps than others, so we introduce an automatic time stepping routine. At initialization of the algorithm, the time step is set heuristically using the characteristic time for the capillary tube case equations, as defined in (2.9). If no cluster has disappeared for three consecutive time steps, the time step is automatically doubled (up to a user-defined maximum). If a cluster disappears during the current time step, the time step is halved until the disappearance occurs exactly at the end of a time step. The disappearance of a cluster introduces many changes that would introduce errors otherwise, in particular with regards to the available diffusion paths, since they are recalculated each time a gas cluster disappears. Enforcing that clusters can only disappear at the end of a time step is also necessary to ensure mass is conserved. A user-defined tolerance on mass flow rates is used to terminate the simulation at what is determined to be the stable equilibrium condition.
The algorithm described in this section is implemented using MATLAB (2014) with an object-oriented programming framework. The numerical values for physical parameters provided in table 1 are representative of storage conditions in a deep saline aquifer.
Table 1. Values for the example simulations are chosen from Chiquet et al. (Reference Chiquet, Daridon, Broseta and Thibeau2007) and Cadogan et al. (Reference Cadogan, Maitland and Trusler2014). We also use
![]() $M=44.0095~\text{g}~\text{mol}^{-1}$
and
$M=44.0095~\text{g}~\text{mol}^{-1}$
and
![]() $R=8.314~\text{J}~\text{K}^{-1}~\text{mol}^{-1}$
. The value for Henry’s constant is determined using pressure and solubility values and is plausible according to Li & Nghiem (Reference Li and Nghiem1986) and Enick & Klara (Reference Enick and Klara1990). In particular, in our setting, the value of the constant in the Krichevsky–Kasarnovsky equation is
$R=8.314~\text{J}~\text{K}^{-1}~\text{mol}^{-1}$
. The value for Henry’s constant is determined using pressure and solubility values and is plausible according to Li & Nghiem (Reference Li and Nghiem1986) and Enick & Klara (Reference Enick and Klara1990). In particular, in our setting, the value of the constant in the Krichevsky–Kasarnovsky equation is
![]() $\exp (\bar{\unicode[STIX]{x1D708}}_{\text{CO}_{2}}^{\infty }/RT)P\approx 1.18$
(where
$\exp (\bar{\unicode[STIX]{x1D708}}_{\text{CO}_{2}}^{\infty }/RT)P\approx 1.18$
(where
![]() $\bar{\unicode[STIX]{x1D708}}_{\text{CO}_{2}}^{\infty }=34~\text{g}~\text{mol}^{-1}$
is the partial molar volume of
$\bar{\unicode[STIX]{x1D708}}_{\text{CO}_{2}}^{\infty }=34~\text{g}~\text{mol}^{-1}$
is the partial molar volume of
![]() $\text{CO}_{2}$
at infinite dilution) so that a value for Henry’s constant of 300 MPa at
$\text{CO}_{2}$
at infinite dilution) so that a value for Henry’s constant of 300 MPa at
![]() $(P,T)=(15~\text{MPa},323.6~\text{K})$
is consistent with figure 1 of Enick & Klara (Reference Enick and Klara1990). We note that this corresponds to a constant of
$(P,T)=(15~\text{MPa},323.6~\text{K})$
is consistent with figure 1 of Enick & Klara (Reference Enick and Klara1990). We note that this corresponds to a constant of
![]() $7.57\times 10^{-5}~\text{mol}~\text{m}^{-3}~\text{Pa}^{-1}$
for the version of Henry’s law that is written
$7.57\times 10^{-5}~\text{mol}~\text{m}^{-3}~\text{Pa}^{-1}$
for the version of Henry’s law that is written
![]() $C=HP$
.
$C=HP$
.

5 Results
5.1 Simulating ganglia evolution
We begin with calculations for simple two-pore body problems to illustrate representative bubble evolution pathways (figure 7). In each case, the pore and pore–throat configuration is identical but different initial bubble sizes/shapes lead to different outcomes. The first row of figure 7 shows the equivalent of Ostwald ripening in a capillary tube case where the bubbles never interact with the solid matrix. As the curvature of the smaller bubble decreases, mass is transferred at a progressively faster rate to the larger bubble. Eventually the smaller bubble disappears and a single-bubble equilibrium is established. This simple case is also used to validate the numerical implementation of the algorithmic framework described in § 4 (labelled pnm), by comparing it to the solution of the simple two bubbles in a capillary tube system described in (2.6) (labelled cap).

Figure 7. Different paths to equilibrium for a simple, symmetric, two-body pore network model. Each row corresponds to a simulation with a different initial condition: two spherical bubbles that never interact with the walls (capillary tube case), the ganglia are both interacting with the solid (case 2), the higher pressure ganglion is interacting with the solid (case 3), the lower pressure ganglion is interacting with the solid (case 4). For each simulation, the first column is the initial condition, the second shows the evolution of interfacial radius for each bubble (
![]() $\unicode[STIX]{x03BC}\text{m}$
) as a function of time (
$\unicode[STIX]{x03BC}\text{m}$
) as a function of time (
![]() $10^{5}$
s), the third shows the evolution of mass for each bubble (
$10^{5}$
s), the third shows the evolution of mass for each bubble (
![]() $10^{-11}$
kg) as a function of time (
$10^{-11}$
kg) as a function of time (
![]() $10^{5}$
s), and the fourth shows the final condition. In the capillary tube case (first row), we show both the solution from the algorithmic framework described in § 4 (labelled pnm), and the solution of the simple two bubbles in a capillary tube system described in (2.6) (labelled cap).
$10^{5}$
s), and the fourth shows the final condition. In the capillary tube case (first row), we show both the solution from the algorithmic framework described in § 4 (labelled pnm), and the solution of the simple two bubbles in a capillary tube system described in (2.6) (labelled cap).
The other cases shown in the last three rows of figure 7 illustrate the stabilizing effect of the solid matrix on bubble evolution. In the second row of figure 7 we show two nearly equally sized bubbles converge to a stable equilibrium with a small amount of mass transfer from the larger to the smaller bubble. In the third row of figure 7 we see the curvature increasing in both bubbles due to mass transfer from the larger to the smaller bubble. Finally, the fourth and last row of figure 7 show the curvature decreasing for both bubbles while mass is being transferred from the smaller to the larger bubble. None of the behaviours shown in the last three rows of figure 7 would occur in a bulk solution, and illustrate the complexity of evolution in situations where the rock walls directly interact with the bubbles.
The overall effect of the interaction with the solid matrix is to stabilize the bubbles. Capillary pressure changes more quickly with changes in mass in the presence of the solid (in this conical geometry) as compared to in a bulk liquid where the bubbles are spheres. Multi-bubble equilibrium is possible with small amounts of mass transfer. We stress that in more complex geometries however, interaction with the solid matrix does not guarantee that ripening will lead to stable end points with disconnected gas ganglia. For example, in a simple two-body network where one body is much larger than the other, ripening will lead to aggregation into a single larger pore body.
In more complex and realistic pore geometries, evolution can be much harder to predict. Consider a ganglion growing into its pore’s adjacent converging conical throats, so that its pressure was lower than that of its neighbours. As the ganglion grows, its pressure increases, which reduces the driving force for the mechanism, and the distance between the ganglia also changes, but in a direction that is difficult to determine qualitatively. As the growing ganglion penetrates farther into the throats it occupies, its shrinking neighbours recede into their own throats, so that the new available distance for diffusion will depend on the particular geometry of the pores the ganglia are centred in, as described by each pore’s individual internal equilibrium curve.

Figure 8. Impact of initial conditions on evolution of ripening systems. (a) Initial condition that leads to equilibrium with disconnected ganglia. (b) Evolution of interface radii for initial conditions in (a). (c) Initial condition that leads to aggregation. (d) Evolution of interface radii for initial conditions in (b). Simulation stops when the orange cluster grows to reach a divergent throat and initiates a Haines jump.
Next we apply the algorithm to more complex and realistic pore geometries. Figure 8 shows results from two simulations in a network generated using the algorithm in appendix B. Parameters for this pore network were extracted from a Berea sandstone microtomography image (Dong & Blunt Reference Dong and Blunt2009). The only difference between the two simulations is in the initial distribution and size of the bubbles. The initial capillary pressure distribution of the bubbles has a mean of 2094 Pa and standard deviation of 60 Pa for figure 8(a), mean of 2770 Pa and standard deviation of 86 Pa for figure 8(c). These are close to the entry pressure of this sandstone rock (Berea), (the entry pressure can be estimated to be of the order of 1300–2200 Pa from the pore throat and pore body radius distributions in figure 10(a,b) (using the interfacial tension in table 1)) as would be expected for residually trapped ganglia of a non-wetting phase (Garing et al. Reference Garing, de Chalendar, Voltolini, Ajo-Franklin and Benson2017a ). We also note that in both cases, these pressures are within the measurement errors in Garing et al. (Reference Garing, de Chalendar, Voltolini, Ajo-Franklin and Benson2017a ), so that both initial conditions would experimentally be considered as equilibrium points for the ripening mechanism.
The differences between these simulations illustrate that without modelling of the ripening mechanism, the evolution of systems of ganglia that interact with the solid is very difficult to predict, since the pore structure and initial conditions play a key role in determining evolution. Although they are very similar, the initial condition in figure 8(a) leads to a stable equilibrium; whereas the one in figure 8(b) does not: the cluster represented in orange grows by absorbing the cluster in red, then continues to grow by absorbing the cluster in green until it can no longer be contained in its pore body, a Haines jump initiates, and the simulation is stopped.
The simulations in figure 8 also allow us to estimate typical time scales for bubble evolution. This is of critical importance for determining the stability of residually trapped
![]() $\text{CO}_{2}$
and for interpreting pore-and-core-scale experiments for measuring residually trapped
$\text{CO}_{2}$
and for interpreting pore-and-core-scale experiments for measuring residually trapped
![]() $\text{CO}_{2}$
(Krevor et al.
Reference Krevor, Blunt, Benson, Pentland, Reynolds, Al-Menhali and Niu2015). If local equilibration occurs quickly, the bubble would be quickly trapped and measurements obtained with short-term experiments would provide reliable estimates of residual trapping. If equilibration is slow, estimates from conventional core flooding experiments may not be reliable because bubble redistribution and potential mobilization may occur on longer time scales than observed in the typical days-to-week long experiments.
$\text{CO}_{2}$
(Krevor et al.
Reference Krevor, Blunt, Benson, Pentland, Reynolds, Al-Menhali and Niu2015). If local equilibration occurs quickly, the bubble would be quickly trapped and measurements obtained with short-term experiments would provide reliable estimates of residual trapping. If equilibration is slow, estimates from conventional core flooding experiments may not be reliable because bubble redistribution and potential mobilization may occur on longer time scales than observed in the typical days-to-week long experiments.
The time scale for equilibration will depend on diffusion paths as well as thermodynamic properties of the wetting and non-wetting phases (density, interfacial tension, solubility). They are consistently longer when evolution leads to a stable end point with disconnected ganglia, since the driving force for equilibration decreases as the curvature of the two bubbles converge. The average half-life for bubble equilibration in the simulations in figure 8 is 2.3 days in the stable case (figure 8
a,b); and 1.04 days in the unstable case (figure 8
c,d) (the half-life for equilibration is defined as the time for the capillary pressure of a bubble to change by
![]() $1/2$
of the difference between its initial and final values).
$1/2$
of the difference between its initial and final values).
We stress that equilibration times are highly sensitive to the properties of the fluids, morphology of the pore network and initial conditions. Nevertheless, for rocks well represented by pore networks with convergent–divergent conical pore throats, equilibration takes place of the order of weeks to months. In order to understand the dependence of equilibration times on the value we choose for Henry’s constant, we run the simulations described in figure 8 with high and low values for Henry’s constant. For
![]() $H=150$
MPa, the half-life of the stable simulation is 1.85 days, compared to 0.94 days for the unstable one. For
$H=150$
MPa, the half-life of the stable simulation is 1.85 days, compared to 0.94 days for the unstable one. For
![]() $H=600$
MPa, the half-life of the stable simulation is 5.6 days, compared to 1.74 days for the unstable one. (Values for
$H=600$
MPa, the half-life of the stable simulation is 5.6 days, compared to 1.74 days for the unstable one. (Values for
![]() $H$
of 150 MPa, respectively 600 MPa, correspond to a solubility of 2.5 %, respectively 10 %, for
$H$
of 150 MPa, respectively 600 MPa, correspond to a solubility of 2.5 %, respectively 10 %, for
![]() $\text{scCO}_{2}$
in brine.)
$\text{scCO}_{2}$
in brine.)
5.2 Upper bound on stable
 $\text{CO}_{2}$
saturations in the case of single-pore spanning ganglia
$\text{CO}_{2}$
saturations in the case of single-pore spanning ganglia
The modelling framework introduced in this paper, and in particular the internal equilibrium concept, can be used to provide upper bounds on the stable saturations of residually trapped
![]() $\text{CO}_{2}$
. In this section, we do not simulate for evolution of ripening systems, but rather look for end points for the mechanism, i.e. partitionings of gaseous
$\text{CO}_{2}$
. In this section, we do not simulate for evolution of ripening systems, but rather look for end points for the mechanism, i.e. partitionings of gaseous
![]() $\text{CO}_{2}$
in the different bodies of a network in such a way that all clusters of gas have the same pore-scale capillary pressure, or equivalently the same interfacial curvature.
$\text{CO}_{2}$
in the different bodies of a network in such a way that all clusters of gas have the same pore-scale capillary pressure, or equivalently the same interfacial curvature.
Extracting an internal equilibrium curve such as the one in figure 5(c) for each pore body in a given network provides crucial information about the structure of the rock represented by that network. In order to further exploit this information, we now make the following three additional assumptions: (i) ganglia can only be stable if they interact with the walls (i.e. we restrict ourselves to mechanisms such as the one labelled case 2 in figure 7); (ii) ganglia span at most one pore; and (iii) bubbles are always trapped (it is possible that bubble growth will lead to remobilization, but that is not considered here). The first assumption is motivated by experimental evidence that the interfacial curvature of residually trapped
![]() $\text{CO}_{2}$
is to a first order determined by the neighbouring pore throats (Andrew et al.
Reference Andrew, Bijeljic and Blunt2014a
; Garing et al.
Reference Garing, de Chalendar, Voltolini, Ajo-Franklin and Benson2017a
), while the second is dictated by our modelling framework.
$\text{CO}_{2}$
is to a first order determined by the neighbouring pore throats (Andrew et al.
Reference Andrew, Bijeljic and Blunt2014a
; Garing et al.
Reference Garing, de Chalendar, Voltolini, Ajo-Franklin and Benson2017a
), while the second is dictated by our modelling framework.
For each of the 2097 pores in figure 9(a), the internal equilibrium curve for the corresponding pore body can be used to describe the volume of
![]() $\text{CO}_{2}$
that could exist in that body as a function of pore-scale capillary pressure (or equivalently interface radius), as described in figure 9(b). At a given pore-scale capillary pressure, repeating this process for each of the bodies in figure 9(a) (restricting the internal equilibrium curves to the volume intervals where the ganglia interact with the solid) amounts to searching the network for the bodies that could accommodate a ganglion with that capillary pressure, as illustrated in figure 9(c). We record the corresponding total gas volumes, and plot the resulting gas saturation as a function of pore-scale capillary pressure in figure 9(d). Since the surface of a stable gas phase must correspond to constant mean curvature surfaces (even for a disconnected gas phase), this plot finally yields an upper bound on stable
$\text{CO}_{2}$
that could exist in that body as a function of pore-scale capillary pressure (or equivalently interface radius), as described in figure 9(b). At a given pore-scale capillary pressure, repeating this process for each of the bodies in figure 9(a) (restricting the internal equilibrium curves to the volume intervals where the ganglia interact with the solid) amounts to searching the network for the bodies that could accommodate a ganglion with that capillary pressure, as illustrated in figure 9(c). We record the corresponding total gas volumes, and plot the resulting gas saturation as a function of pore-scale capillary pressure in figure 9(d). Since the surface of a stable gas phase must correspond to constant mean curvature surfaces (even for a disconnected gas phase), this plot finally yields an upper bound on stable
![]() $\text{CO}_{2}$
saturations in this network, under the assumption that the disconnected gas ganglia span at most one pore. The low saturations observed on this plot confirm experimental observations that for residual saturations of 10 %–30 %, the non-wetting phase must take the form of large clusters that occupy multiple pores (Iglauer et al.
Reference Iglauer, Paluszny, Pentland and Blunt2011; Garing et al.
Reference Garing, de Chalendar, Voltolini, Ajo-Franklin and Benson2017a
).
$\text{CO}_{2}$
saturations in this network, under the assumption that the disconnected gas ganglia span at most one pore. The low saturations observed on this plot confirm experimental observations that for residual saturations of 10 %–30 %, the non-wetting phase must take the form of large clusters that occupy multiple pores (Iglauer et al.
Reference Iglauer, Paluszny, Pentland and Blunt2011; Garing et al.
Reference Garing, de Chalendar, Voltolini, Ajo-Franklin and Benson2017a
).

Figure 9. Extracting more information from the internal equilibrium curves. (a) Visualization for an example stochastic network generated using data from a network extracted from a Berea sandstone microCT image (Dong & Blunt Reference Dong and Blunt2009). Porosity is 32.7 %. (b) Calculation of volume as a function of interfacial radius using an internal equilibrium curve (restricted to the volume interval such that the ganglion interacts with the solid). (c) For a given interfacial radius, calculation of maximum total volume that can be stable in the 2087 pore bodies of the network. (d) Upper bound on the residual
![]() $\text{CO}_{2}$
saturation as a function of capillary pressure in the case where gas ganglia occupy at most one pore.
$\text{CO}_{2}$
saturation as a function of capillary pressure in the case where gas ganglia occupy at most one pore.
6 Discussion
Whereas in the capillary tube setting thermodynamic equilibrium is only reached when the gas phase aggregates to form a single spherical bubble, in porous media equilibrium situations with disconnected gas ganglia are theoretically possible. The major difference between the two cases lies in the relationship between the mass and capillary pressure variables. Whereas in the capillary tube liquid case, a decrease in mass results in an increase in capillary pressure, the relationship is much more complex in the presence of a solid matrix. In rocks, pore-scale capillary pressure gradients, diffusion paths and pore structure are found to be key in determining evolution. The results in this paper are applicable to rocks that are well represented by pore network models: if throats can be represented as converging conical frusta, a decrease in mass results in a decrease in capillary pressure, which has a stabilizing effect. This stabilizing effect as well as the experimental observation that the system is likely to be initialized with gas clusters that are interacting with the solid matrix (Garing et al. Reference Garing, de Chalendar, Voltolini, Ajo-Franklin and Benson2017a ) suggest that at a local scale the ripening of disconnected ganglia is unlikely to cause the bubbles to remobilize as long as the medium is homogeneous.
We then search the pore space for stable equilibrium states to estimate the maximal saturations that can be residually trapped in a rock. The maximum saturation of 8 % shown in figure 9(c) is quite low, which leads us to conclude that stable end points with higher saturations of 10 %–30 % necessarily correspond to a cluster size distribution where some ganglia span multiple pores (such ganglia are frequently observed in residual trapping experiments (Iglauer et al.
Reference Iglauer, Paluszny, Pentland and Blunt2011; Garing et al.
Reference Garing, de Chalendar, Voltolini, Ajo-Franklin and Benson2017a
)). These plots give yet another indication of the impact of pore structure on the ripening mechanism, since the range of available capillary pressures that a pore body can accommodate is determined to a large extent by body-to-throat aspect ratio. We expect that rocks with higher aspect ratios will have higher maximal
![]() $\text{CO}_{2}$
saturations as defined by figure 9(c) and as such are better able to effectively trap
$\text{CO}_{2}$
saturations as defined by figure 9(c) and as such are better able to effectively trap
![]() $\text{CO}_{2}$
.
$\text{CO}_{2}$
.
A natural extension of this model would be to include ganglia spanning multiple pores. In order to do so, we need to determine how much mass is transferred when a ganglion interacting with a throat shaped like a converging conical frustum grows in a quasistatic manner until it reaches a portion of a throat shaped like a diverging conical frustum and initiates the instability referred to as a Haines jump (Haines Reference Haines1930). Micromodel experimentation is one path forward to do so. Another limitation of this work is that when the network becomes sparsely populated, the number of paths grows exponentially, which makes finding diffusion paths computationally intractable. Finding an alternative way of modelling diffusion to overcome this computational barrier for large networks would be another significant step forward.
7 Conclusions and implications for
 $\text{CO}_{2}$
storage
$\text{CO}_{2}$
storage
This paper presents a novel simulation framework to study the effect of pore-scale Ostwald ripening on the stability of residually trapped
![]() $\text{scCO}_{2}$
, a critical question in the context of the geological storage of carbon dioxide. We use this framework to demonstrate stability is possible; quantify the importance of pore structure; provide an upper bound on the stable saturations of trapped
$\text{scCO}_{2}$
, a critical question in the context of the geological storage of carbon dioxide. We use this framework to demonstrate stability is possible; quantify the importance of pore structure; provide an upper bound on the stable saturations of trapped
![]() $\text{scCO}_{2}$
in the case of single-pore spanning ganglia; and finally estimate typical evolution times for ripening in a Berea sandstone.
$\text{scCO}_{2}$
in the case of single-pore spanning ganglia; and finally estimate typical evolution times for ripening in a Berea sandstone.
The framework decomposes the Ostwald ripening mechanism into two processes that operate on different time scales and significantly extends the predictive capabilities of traditional pore network models where an accurate description of the mechanism was not previously possible. The methodological approach presented here provides a foundation to study ripening in porous media that are well represented by the pore network representation. Results suggest that evolution time scales are sensitive to both available diffusion paths and the thermodynamic properties of the wetting and non-wetting phases; and can vary significantly, depending on the type of rock. In the context of the geological sequestration of carbon dioxide however, even evolution time scales of several years could be relevant to storage security.
Acknowledgements
Funding for this research is supported by the Department of Energy, Office of Basic Energy Sciences Energy Frontier Research Center under contract number DE-AC02-05CH11231 and the Global Climate and Energy Project. We thank the anonymous reviewers for their thorough review and thoughtful comments that resulted in a significant modification of our initial submission and a much improved manuscript.
Appendix A. Brief review of previous theoretical frameworks for Ostwald ripening
Previous work on the Ostwald ripening problem (Greenwood Reference Greenwood1956; Lifshitz & Slyozov Reference Lifshitz and Slyozov1961; Voorhees Reference Voorhees1985; Schmelzer & Schweitzer Reference Schmelzer and Schweitzer1987; Schmelzer et al. Reference Schmelzer and Möller1995) is commonly based on the Ostwald–Freundlich equation, which uses the following relation between a liquid and its vapour (Thomson Reference Thomson1872):
where
![]() $p_{g}$
is the pressure in the gas,
$p_{g}$
is the pressure in the gas,
![]() $p_{l}$
is the pressure in the liquid,
$p_{l}$
is the pressure in the liquid,
![]() $\unicode[STIX]{x1D70E}$
is interfacial tension,
$\unicode[STIX]{x1D70E}$
is interfacial tension,
![]() $\unicode[STIX]{x1D70C}_{g}$
, respectively
$\unicode[STIX]{x1D70C}_{g}$
, respectively
![]() $\unicode[STIX]{x1D70C}_{l}$
, is the density of the gas phase, respectively of the liquid phase and
$\unicode[STIX]{x1D70C}_{l}$
, is the density of the gas phase, respectively of the liquid phase and
![]() $R$
is the radius of the interface. Using the assumptions that (i) the gas is ideal, (ii)
$R$
is the radius of the interface. Using the assumptions that (i) the gas is ideal, (ii)
![]() $\unicode[STIX]{x1D70C}_{l}\gg \unicode[STIX]{x1D70C}_{g}$
and (iii)
$\unicode[STIX]{x1D70C}_{l}\gg \unicode[STIX]{x1D70C}_{g}$
and (iii)
![]() $(p_{g}(R)-p_{l})/p_{l}\ll 1$
, we can derive the Thomson–Freundlich (also called Ostwald–Freundlich) equation:
$(p_{g}(R)-p_{l})/p_{l}\ll 1$
, we can derive the Thomson–Freundlich (also called Ostwald–Freundlich) equation:
where
![]() $p$
can be partial pressure, concentration or chemical potential. This equation highlights the existence of a critical radius for which the system is at equilibrium. It is derived for a single component system, and using the assumption that the gas is an ideal gas.
$p$
can be partial pressure, concentration or chemical potential. This equation highlights the existence of a critical radius for which the system is at equilibrium. It is derived for a single component system, and using the assumption that the gas is an ideal gas.
Greenwood (Reference Greenwood1956) used the Thomson–Freundlich equation as a starting point to study the growth of solid particles in liquid solutions:
with
![]() $S$
the true solubility,
$S$
the true solubility,
![]() $S_{a}$
the solubility in contact with a particle of radius
$S_{a}$
the solubility in contact with a particle of radius
![]() $a$
,
$a$
,
![]() $\unicode[STIX]{x1D70C}$
density,
$\unicode[STIX]{x1D70C}$
density,
![]() $M$
molecular weight,
$M$
molecular weight,
![]() $\unicode[STIX]{x1D70E}$
interfacial tension. Since the difference between
$\unicode[STIX]{x1D70E}$
interfacial tension. Since the difference between
![]() $S$
and
$S$
and
![]() $S_{a}$
is small, the difference between the solubilities in contact with two different particles of radius
$S_{a}$
is small, the difference between the solubilities in contact with two different particles of radius
![]() $a_{1}$
and
$a_{1}$
and
![]() $a_{2}$
is then written as:
$a_{2}$
is then written as:
Using Fick’s law, Greenwood (Reference Greenwood1956) then derives the following equation for the evolution of the radius of a particle in a system of
![]() $n$
particles:
$n$
particles:
with
![]() $(A/x)$
the effective area to length ratio of the diffusion path between two particles. Using a spherical diffusion regime, conservation of mass and assuming that the grains are far away from each other leads to equation (7) in Greenwood (Reference Greenwood1956):
$(A/x)$
the effective area to length ratio of the diffusion path between two particles. Using a spherical diffusion regime, conservation of mass and assuming that the grains are far away from each other leads to equation (7) in Greenwood (Reference Greenwood1956):
with
![]() $a_{m}$
the arithmetic mean radius of the system of
$a_{m}$
the arithmetic mean radius of the system of
![]() $n$
particles. We note that this corresponds to
$n$
particles. We note that this corresponds to
![]() $\sum _{i=1}^{n}(A/x)_{i}=4\unicode[STIX]{x03C0}a$
and that this is valid in a system where the particles are highly dispersed.
$\sum _{i=1}^{n}(A/x)_{i}=4\unicode[STIX]{x03C0}a$
and that this is valid in a system where the particles are highly dispersed.
A major breakthrough in the study of the Ostwald ripening phenomenon was the seminal paper by Lifshitz & Slyozov (Reference Lifshitz and Slyozov1961), who consider a slightly supersaturated solution, and were able to make quantitative predictions on the asymptotic behaviour of coarsening systems without explicitly solving the relevant equations. They consider diffusion currents between the grains and the solution, and start from the equation:
where
![]() $C_{R}$
is the concentration in contact with a particle of radius
$C_{R}$
is the concentration in contact with a particle of radius
![]() $R$
,
$R$
,
![]() $C_{\infty }$
is the concentration of the saturated solution and
$C_{\infty }$
is the concentration of the saturated solution and
![]() $\unicode[STIX]{x1D708}$
is the atomic volume of the solute. Equation (A 7) is used with Fick’s law and conservation of mass (assuming that no new particles appear) to derive a governing equation for the particle radius distribution function
$\unicode[STIX]{x1D708}$
is the atomic volume of the solute. Equation (A 7) is used with Fick’s law and conservation of mass (assuming that no new particles appear) to derive a governing equation for the particle radius distribution function
![]() $f$
. At long times, it is then shown that the distribution function
$f$
. At long times, it is then shown that the distribution function
![]() $f$
verifies an ordinary differential equation, which can be solved to make predictions on the long-term evolution of the mean and critical radii. We note that the Lifschitz–Slyozov, or Lifschitz–Slyozov–Wagner (LSW) theory, like Greenwood (Reference Greenwood1956), considers that grains are far enough that a spherical diffusion regime can be considered, and establishes asymptotic results on the evolution of the radius distribution function. A review of this classic theory and of subsequent results is given in Voorhees (Reference Voorhees1985). Some attempts were later made to extend this theory to porous media, e.g. in Schmelzer et al. (Reference Schmelzer and Möller1995), which builds off the same equations as in the LSW theory but then assumes growth stops or is strongly inhibited as soon as the growing grains start interacting with the solid matrix.
$f$
verifies an ordinary differential equation, which can be solved to make predictions on the long-term evolution of the mean and critical radii. We note that the Lifschitz–Slyozov, or Lifschitz–Slyozov–Wagner (LSW) theory, like Greenwood (Reference Greenwood1956), considers that grains are far enough that a spherical diffusion regime can be considered, and establishes asymptotic results on the evolution of the radius distribution function. A review of this classic theory and of subsequent results is given in Voorhees (Reference Voorhees1985). Some attempts were later made to extend this theory to porous media, e.g. in Schmelzer et al. (Reference Schmelzer and Möller1995), which builds off the same equations as in the LSW theory but then assumes growth stops or is strongly inhibited as soon as the growing grains start interacting with the solid matrix.
Appendix B. Generation of stochastic network models
In this section we present an algorithm to generate stochastic network models that are statistically representative of real rocks. As in Idowu (Reference Idowu2009), we target statistical properties that are commonly available from microCT imaging. In particular, we seek to generate networks where the probability distribution functions (p.d.f.) for certain macroscopic parameters match those of a network derived from a real rock: (i) body radius, (ii) throat radius, (iii) coordination number and (iv) throat length. The network model shown in figure 9 was generated using the algorithm we developed. The network consists in 2026 bodies linked by 4213 throats, for a total porosity of 32.7 %. It was generated using code made available online (de Chalendar Reference de Chalendar2016b ) and data from a Berea sandstone network extracted using Dong & Blunt (Reference Dong and Blunt2009). In figure 10, we show the target and generated statistical properties for the network in figure 9.

Figure 10. Statistical properties of the stochastically generated network in figure 9. (a) Pore body radius (
![]() $\unicode[STIX]{x03BC}\text{m}$
). (b) Pore throat radius (
$\unicode[STIX]{x03BC}\text{m}$
). (b) Pore throat radius (
![]() $\unicode[STIX]{x03BC}\text{m}$
). (c) Throat length (
$\unicode[STIX]{x03BC}\text{m}$
). (c) Throat length (
![]() $\unicode[STIX]{x03BC}\text{m}$
). (d) Coordination number. (e) Correlation between radius of body and average radius for the connecting throats.
$\unicode[STIX]{x03BC}\text{m}$
). (d) Coordination number. (e) Correlation between radius of body and average radius for the connecting throats.
B.1 Algorithm
The main steps of the algorithm we have developed to generate stochastic network models are summarized in the following.
-
(i) Define a bounding box for the pore space.
-
(ii) Generate bodies. Body centres are generated using random sampling in the bounding box. Body radii are drawn from the body radius p.d.f. As each new body is generated, its distance to all the other bodies is stored (if it is too close to one of the previous bodies, the current one is discarded). Bodies are generated until a target porosity is reached.
-
(iii) Draw random samples from the coordination number p.d.f. until we have as many coordination numbers as bodies.
-
(iv) Choose a weight for each body. For example, we use the distance to the
 $n$
th closest neighbouring body, where
$n$
th closest neighbouring body, where
 $n$
is the highest coordination number we drew (another possible choice is given in Idowu & Blunt Reference Idowu and Blunt2010).
$n$
is the highest coordination number we drew (another possible choice is given in Idowu & Blunt Reference Idowu and Blunt2010). -
(v) Assign coordination numbers to the bodies based on the body weights.
-
(vi) Generate connections. Continually select bodies at random in those that have connections left to make. Draw a target throat length from the throat length p.d.f. Use the distance matrix created in step 2 to find the connection that corresponds to the closest throat length in the connections that have not been made yet.
-
(vii) Draw random sample from the throat radius p.d.f. until we have as many radii as connections.
-
(viii) Choose a weight for each connection. We use the smallest of the radii of the bodies that are connected by each throat.
-
(ix) Assign radii to the throats based on the throat weights. We enforce that all throats must have a smaller radius than the bodies it connects.
Appendix C. Expression for
 $V_{con}^{i}(R_{cl})$
$V_{con}^{i}(R_{cl})$
We redefine some variables for the purpose of this derivation. We consider an interface that is in throat
![]() $i$
,
$i$
,
![]() $i=1\ldots n$
. We call
$i=1\ldots n$
. We call
![]() $R^{i}$
the radius of the interface and
$R^{i}$
the radius of the interface and
![]() $r^{i}$
the radius of the conical frustum at the location of the interface;
$r^{i}$
the radius of the conical frustum at the location of the interface;
![]() $h_{max}^{i}$
the length of throat
$h_{max}^{i}$
the length of throat
![]() $i$
; and
$i$
; and
![]() $h^{i}$
the position of the interface in throat
$h^{i}$
the position of the interface in throat
![]() $i$
with
$i$
with
![]() $h_{i}\in [0,h_{max}^{i}]$
.
$h_{i}\in [0,h_{max}^{i}]$
.
The volume of gas in the conical frustum
![]() $V_{con}^{i}$
can be expressed as (we neglect the volume of the spherical cap):
$V_{con}^{i}$
can be expressed as (we neglect the volume of the spherical cap):
The relation between tube radius and interface radius is given by
We call
![]() $R_{cl}$
the equilibrium interface radius. We have
$R_{cl}$
the equilibrium interface radius. We have
![]() $\forall i=1\ldots n,R_{cl}=R^{i}$
so
$\forall i=1\ldots n,R_{cl}=R^{i}$
so
We also write the relation between position and tube radius using linear interpolation:
so that we can also express
![]() $h^{i}$
as a function of
$h^{i}$
as a function of
![]() $R_{cl}$
$R_{cl}$
Finally, we can express the volume of the ganglion that is in the conical frustum as a function of the equilibrium interface radius:
 $$\begin{eqnarray}\displaystyle V_{con}^{i}(R_{cl}) & = & \displaystyle \frac{\unicode[STIX]{x03C0}}{3}\frac{h_{max}^{i}}{r_{th}^{i}-r_{b,th}^{i}}[R_{cl}\cos (\unicode[STIX]{x1D703}+\unicode[STIX]{x1D719}^{i})-r_{b,th}^{i}]\nonumber\\ \displaystyle & & \displaystyle \times \,[{r_{b,th}^{i}}^{2}+r_{b,th}^{i}R_{cl}\cos (\unicode[STIX]{x1D703}+\unicode[STIX]{x1D719}^{i})+(R_{cl}\cos (\unicode[STIX]{x1D703}+\unicode[STIX]{x1D719}^{i}))^{2}].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle V_{con}^{i}(R_{cl}) & = & \displaystyle \frac{\unicode[STIX]{x03C0}}{3}\frac{h_{max}^{i}}{r_{th}^{i}-r_{b,th}^{i}}[R_{cl}\cos (\unicode[STIX]{x1D703}+\unicode[STIX]{x1D719}^{i})-r_{b,th}^{i}]\nonumber\\ \displaystyle & & \displaystyle \times \,[{r_{b,th}^{i}}^{2}+r_{b,th}^{i}R_{cl}\cos (\unicode[STIX]{x1D703}+\unicode[STIX]{x1D719}^{i})+(R_{cl}\cos (\unicode[STIX]{x1D703}+\unicode[STIX]{x1D719}^{i}))^{2}].\end{eqnarray}$$
This last relation gives the volume of the ganglion as a cubic polynomial of the equilibrium interface radius. There are three possible solutions to this equation. In practice, we find there is only one solution in the interval
![]() $[R_{min},R_{max}]$
, where
$[R_{min},R_{max}]$
, where
![]() $R_{min}$
is the interface radius defined by the limiting throat and
$R_{min}$
is the interface radius defined by the limiting throat and
![]() $R_{max}$
is the radius of the body
$R_{max}$
is the radius of the body
![]() $r_{B}$
. Note that to find the maximum available volume
$r_{B}$
. Note that to find the maximum available volume
![]() $V_{B}^{max}$
we do not need to solve an internal equilibrium problem. Since we know that for this volume the radius of the interface is the one defined by the limiting throat, we can directly calculate the volume
$V_{B}^{max}$
we do not need to solve an internal equilibrium problem. Since we know that for this volume the radius of the interface is the one defined by the limiting throat, we can directly calculate the volume
![]() $V_{B}^{max}$
using (C 6).
$V_{B}^{max}$
using (C 6).














