Published online by Cambridge University Press: 01 May 2012
The first generation of stars had very different properties than later stellar generations, as they formed from a ‘pristine’ gas that was completely free of heavy elements. Normal star formation took place only after the first stars had polluted the surrounding turbulent interstellar gas, increasing its local heavy-element mass concentration, 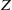 , beyond a ‘critical’ threshold value,
, beyond a ‘critical’ threshold value, 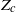 (
(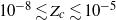 ). Motivated by this astrophysical problem, we investigate the fundamental physics of the pollution of pristine fluid elements in statistically homogeneous and isotropic compressible turbulence. Turbulence stretches the pollutants, produces concentration structures at small scales, and brings the pollutants and the unpolluted flow in closer contact. The pristine material is polluted when exposed to the pollutant sources or the fluid elements polluted by previous mixing events. Our theoretical approach employs the probability distribution function (p.d.f.) method for turbulent mixing, as the fraction of pristine mass corresponds to the low tail of the density-weighted concentration p.d.f. We adopt a number of p.d.f. closure models and derive evolution equations for the pristine fraction from the models. To test and constrain the prediction of theoretical models, we conduct numerical simulations for decaying passive scalars in isothermal turbulent flows with Mach numbers of 0.9 and 6.2, and compute the mass fraction,
). Motivated by this astrophysical problem, we investigate the fundamental physics of the pollution of pristine fluid elements in statistically homogeneous and isotropic compressible turbulence. Turbulence stretches the pollutants, produces concentration structures at small scales, and brings the pollutants and the unpolluted flow in closer contact. The pristine material is polluted when exposed to the pollutant sources or the fluid elements polluted by previous mixing events. Our theoretical approach employs the probability distribution function (p.d.f.) method for turbulent mixing, as the fraction of pristine mass corresponds to the low tail of the density-weighted concentration p.d.f. We adopt a number of p.d.f. closure models and derive evolution equations for the pristine fraction from the models. To test and constrain the prediction of theoretical models, we conduct numerical simulations for decaying passive scalars in isothermal turbulent flows with Mach numbers of 0.9 and 6.2, and compute the mass fraction, 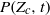 , of the flow with
, of the flow with 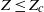 . In the Mach 0.9 flow, the evolution of
. In the Mach 0.9 flow, the evolution of 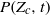 is well-described by a continuous convolution model and goes as
is well-described by a continuous convolution model and goes as 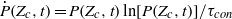 , if the mass fraction of the polluted flow is larger than
, if the mass fraction of the polluted flow is larger than 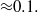 If the initial pollutant fraction is smaller than
If the initial pollutant fraction is smaller than 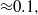 an early phase exists during which the pristine fraction follows an equation derived from a nonlinear integral model:
an early phase exists during which the pristine fraction follows an equation derived from a nonlinear integral model: 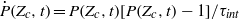 . The time scales
. The time scales 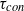 and
and 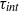 are measured from our simulations. When normalized to the flow dynamical time, the decay of
are measured from our simulations. When normalized to the flow dynamical time, the decay of 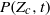 in the Mach 6.2 flow is slower than at Mach 0.9 because the time scale for scalar variance decay is slightly larger and the low tail of the concentration p.d.f. broadens with increasing Mach number. We show that
in the Mach 6.2 flow is slower than at Mach 0.9 because the time scale for scalar variance decay is slightly larger and the low tail of the concentration p.d.f. broadens with increasing Mach number. We show that 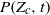 in the Mach 6.2 flow can be well fitted using a formula from a generalized version of the self-convolution model.
in the Mach 6.2 flow can be well fitted using a formula from a generalized version of the self-convolution model.