Published online by Cambridge University Press: 17 November 2017
We investigate the excitation and radiation of near-inertial internal gravity waves continuously excited by a latitudinally confined temporally fluctuating wind in a numerical model of a stratified ocean on a 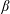 $\unicode[STIX]{x1D6FD}$-plane at mid-latitude. The surface wind forcing contains both high- and low-frequency components which excite propagating waves and a baroclinically unstable zonal jet respectively. Wentzel–Kramers–Brillouin (WKB) ray theory implies that near-inertial waves propagate strictly towards the equator. We seek to refine this view here by (i) adding the non-traditional Coriolis force (accounting for the horizontal component of the Earth’s rotation) into the equations of motion, in order to allow poleward sub-inertial propagation to occur, and (ii) relaxing the conceptual constraint of no zonal variability, to allow the zonal jet to undergo instability, to meander and to sustain an active field of mesoscale eddies, potentially impacting the excitation of near-inertial waves. The key results are that, while (i) permits weakly stratified waveguides with sub-inertial poleward wave propagation to develop in accord with theory, the sub-inertial energy flux observed is very small compared with the equatorward flux. Thus, in terms of energy radiated from the storm track, non-traditional effects are small for wind-driven near-inertial waves. The consequences of (ii) are much more pronounced. Refinement (ii) produces a radiating wave field that is bidirectional, i.e. with both poleward and equatorward components. We show that the presence of regions of significant background vorticity with horizontal scales significantly smaller than the width of the storm track provides the scale selection mechanism to excite waves with sufficiently super-inertial frequencies to propagate poleward distances of the order of 1000 km.
$\unicode[STIX]{x1D6FD}$-plane at mid-latitude. The surface wind forcing contains both high- and low-frequency components which excite propagating waves and a baroclinically unstable zonal jet respectively. Wentzel–Kramers–Brillouin (WKB) ray theory implies that near-inertial waves propagate strictly towards the equator. We seek to refine this view here by (i) adding the non-traditional Coriolis force (accounting for the horizontal component of the Earth’s rotation) into the equations of motion, in order to allow poleward sub-inertial propagation to occur, and (ii) relaxing the conceptual constraint of no zonal variability, to allow the zonal jet to undergo instability, to meander and to sustain an active field of mesoscale eddies, potentially impacting the excitation of near-inertial waves. The key results are that, while (i) permits weakly stratified waveguides with sub-inertial poleward wave propagation to develop in accord with theory, the sub-inertial energy flux observed is very small compared with the equatorward flux. Thus, in terms of energy radiated from the storm track, non-traditional effects are small for wind-driven near-inertial waves. The consequences of (ii) are much more pronounced. Refinement (ii) produces a radiating wave field that is bidirectional, i.e. with both poleward and equatorward components. We show that the presence of regions of significant background vorticity with horizontal scales significantly smaller than the width of the storm track provides the scale selection mechanism to excite waves with sufficiently super-inertial frequencies to propagate poleward distances of the order of 1000 km.