Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-29T07:23:47.843Z Has data issue: false hasContentIssue false
  • English
  • Français

Phoretic motion in active matter

Published online by Cambridge University Press:  05 July 2021

John F. Brady Open the ORCID record for John F. Brady [Opens in a new window]
John F. Brady*
Affiliation:
Divisions of Chemistry & Chemical Engineering and Engineering & Applied Science, California Institute of Technology, Pasadena, CA91125, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

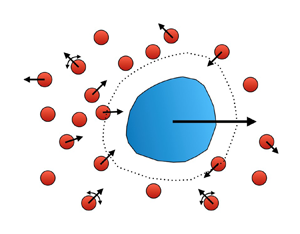
A new continuum perspective for phoretic motion is developed that is applicable to particles of any shape in ‘microstructured’ fluids such as a suspension of solute or bath particles. Using the reciprocal theorem for Stokes flow it is shown that the local osmotic pressure of the solute adjacent to the phoretic particle generates a thrust force (via a ‘slip’ velocity) which is balanced by the hydrodynamic drag such that there is no net force on the body. For a suspension of passive Brownian bath particles this perspective recovers the classical result for the phoretic velocity owing to an imposed concentration gradient. In a bath of active particles that self-propel with characteristic speed $U_0$ for a time $\tau _R$ and then change direction randomly, taking a step of size $\ell = U_0 \tau _R$, at high activity the phoretic velocity is $\boldsymbol {U} \sim - U_0 \ell \boldsymbol {\nabla } \phi _b$, where $\phi _b$ is a measure of the ‘volume’ fraction of the active bath particles. The phoretic velocity is independent of the size of the phoretic particle and of the viscosity of the suspending fluid. Because active systems are inherently out of equilibrium, phoretic motion can occur even without an imposed concentration gradient. It is shown that at high activity when the run length varies spatially, net phoretic motion results in $\boldsymbol {U} \sim - \phi _b U_0 \boldsymbol {\nabla } \ell$. These two behaviours are special cases of the more general result that phoretic motion arises from a gradient in the swim pressure of active matter. Finally, it is shown that a field that orients (but does not propel) the active particles results in a phoretic velocity $\boldsymbol {U} \sim - \phi _b U_0 \ell \boldsymbol {\nabla }\varPsi$, where $\varPsi$ is the (non-dimensional) potential associated with the field.

JFM classification

Complex Fluids: Active matter Complex Fluids: Colloids Complex Fluids: Suspensions
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 922 , 10 September 2021 , A10
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Anderson, J.L. 1989 Colloid transport by interfacial forces. Annu. Rev. Fluid Mech. 21 (1), 61–99.CrossRefGoogle Scholar
Angelani, L, Costanzo, A & Di Leonardo, R. 2011 Active ratchets. Europhys. Lett. 96 (6), 68002.CrossRefGoogle Scholar
Arlt, J., Martinez, V.A., Dawson, A., Pilizota, T. & Poon, W.C.K. 2018 Painting with light-powered bacteria. Nat. Commun. 9 (1), 768.CrossRefGoogle ScholarPubMed
Arlt, J., Martinez, V.A., Dawson, A., Pilizota, T. & Poon, W.C.K. 2019 Dynamics-dependent density distribution in active suspensions. Nat. Commun. 10 (1), 2321.CrossRefGoogle ScholarPubMed
Bechinger, C., Di Leonardo, R., Löwen, H., Reichhardt, C., Volpe, G. & Volpe, G. 2016 Active particles in complex and crowded environments. Rev. Mod. Phys. 88 (4), 045006.CrossRefGoogle Scholar
Bialké, J., Löwen, H. & Speck, T. 2013 Microscopic theory for the phase separation of self-propelled repulsive disks. Europhys. Lett. 103 (3), 30008.CrossRefGoogle Scholar
Brady, J.F. 2011 Particle motion driven by solute gradients with application to autonomous motion: continuum and colloidal perspectives. J. Fluid Mech. 667, 216–259.CrossRefGoogle Scholar
Burkholder, E.W. & Brady, J.F. 2018 Do hydrodynamic interactions affect the swim pressure? Soft Matt. 14, 3581–3589.CrossRefGoogle ScholarPubMed
Buttinoni, I., Bialké, J., Kümmel, F., Löwen, H., Bechinger, C. & Speck, T. 2013 Dynamical clustering and phase separation in suspensions of self-propelled colloidal particles. Phys. Rev. Lett. 110, 238301.CrossRefGoogle ScholarPubMed
Cates, M.E., Marenduzzo, D., Pagonabarraga, I. & Tailleur, J. 2010 Arrested phase separation in reproducing bacteria creates a generic route to pattern formation. Proc. Natl Acad. Sci. USA 107 (26), 11715–11720.CrossRefGoogle ScholarPubMed
Córdova-Figueroa, U.M. & Brady, J.F. 2008 Osmotic propulsion: the osmotic motor. Phys. Rev. Lett. 100 (15), 158303.CrossRefGoogle ScholarPubMed
Dhont, J.K.G. 2004 Thermodiffusion of interacting colloids. I. A statistical thermodynamics approach. J. Chem. Phys. 120 (3), 1632–1641.CrossRefGoogle ScholarPubMed
Digregorio, P., Levis, D., Suma, A., Cugliandolo, L.F., Gonnella, G. & Pagonabarraga, I. 2018 Full phase diagram of active Brownian disks: from melting to motility-induced phase separation. Phys. Rev. Lett. 121 (9), 098003.CrossRefGoogle ScholarPubMed
Fily, Y. & Marchetti, M.C. 2012 Athermal phase separation of self-propelled particles with no alignment. Phys. Rev. Lett. 108 (23), 235702.CrossRefGoogle ScholarPubMed
Frangipane, G., Dell'Arciprete, D., Petracchini, S., Maggi, C., Saglimbeni, F., Bianchi, S., Vizsnyiczai, G., Bernardini, M.L. & di Leonardo, R. 2018 Dynamic density shaping of photokinetic E. Coli. Elife 7, 1–14.CrossRefGoogle ScholarPubMed
Gomper, G., et al. 2020 The 2020 motile active matter roadmap. J. Phys.: Condens. Matter 32 (19), 193001.Google Scholar
Guo, S., Samanta, D., Peng, Y., Xu, X. & Cheng, X. 2018 Symmetric shear banding and swarming vortices in bacterial superfluids. Proc. Natl Acad. Sci. USA 115 (28), 7212–7217.CrossRefGoogle ScholarPubMed
Howse, J.R., Jones, R.A.L., Ryan, A.J., Gough, T., Vafabakhsh, R. & Golestanian, R. 2007 Self-motile colloidal particles: from directed propulsion to random walk. Phys. Rev. Lett. 99 (4), 048102.CrossRefGoogle ScholarPubMed
Kaiser, A., Sokolov, A., Aranson, I.S. & Löwen, H. 2015 Motion of two micro-wedges in a turbulent bacterial bath. Eur. Phys. J.: Spec. Top. 224 (7), 1275–1286.Google Scholar
Kjeldbjerg, C.M. & Brady, J.F. 2021 Theory for the Casimir effect and the partitioning of active matter. Soft Matt. 17 (3), 523–530.CrossRefGoogle ScholarPubMed
Lauga, E. & Powers, T.R. 2009 The hydrodynamics of swimming microorganisms. Rep. Prog. Phys. 72, 096601.CrossRefGoogle Scholar
Lushi, E., Goldstein, R.E. & Shelley, M.J. 2012 Collective chemotactic dynamics in the presence of self-generated fluid flows. Phys. Rev. E 86 (4), 040902.CrossRefGoogle ScholarPubMed
Marbach, S., Yoshida, H. & Bocquet, L. 2020 Local and global force balance for diffusiophoretic transport. J. Fluid Mech. 892, A6.CrossRefGoogle ScholarPubMed
Marchetti, M.C., Joanny, J.F., Ramaswamy, S., Liverpool, T.B., Prost, J., Rao, M. & Simha, R.A. 2013 Hydrodynamics of soft active matter. Rev. Mod. Phys. 85 (3), 1143–1189.CrossRefGoogle Scholar
Palacci, J., Sacanna, S., Steinberg, A.P., Pine, D.J. & Chaikin, P.M. 2013 Living crystals of light-activated colloidal surfers. Science 339 (6122), 936–940.CrossRefGoogle ScholarPubMed
Paxton, W.F., Kistler, K.C., Olmeda, C.C., Sen, A., St. Angelo, S.K., Cao, Y., Mallouk, T.E., Lammert, P.E. & Crespi, V.H. 2004 Catalytic nanomotors: autonomous movement of striped nanorods. J. Am. Chem. Soc. 126 (41), 13424–13431.CrossRefGoogle ScholarPubMed
Ramaswamy, S. 2010 The mechanics and statistics of active matter. Annu. Rev. Condens. Matter Phys. 1 (1), 323–345.CrossRefGoogle Scholar
Razin, N., Voituriez, R., Elgeti, J. & Gov, N.S. 2017 Generalized Archimedes’ principle in active fluids. Phys. Rev. E 96, 032606.CrossRefGoogle ScholarPubMed
Row, H. & Brady, J.F. 2020 Reverse osmotic effect in active matter. Phys. Rev. E 101, 062604.CrossRefGoogle ScholarPubMed
Saintillan, D. & Shelley, M.J. 2015 Theory of active suspensions. In Complex Fluids in Biological Systems (ed. S.E. Spagnolie), chap. 9, pp. 319–355. Springer.CrossRefGoogle Scholar
Schnitzer, M.J. 1993 Theory of continuum random walks and application to chemotaxis. Phys. Rev. E 48 (4), 2553–2568.CrossRefGoogle ScholarPubMed
Shklyaev, S., Brady, J.F. & Córdova-Figueroa, U.M. 2014 Non-spherical osmotic motor: chemical sailing. J. Fluid Mech. 748, 2488–520.CrossRefGoogle Scholar
Squires, T.M. & Brady, J.F. 2005 A simple paradigm for active and nonlinear microrheology. Phys. Fluids 17 (7), 073101–073121.CrossRefGoogle Scholar
Stenhammar, J., Tiribocchi, A., Allen, R.J., Marenduzzo, D. & Cates, M.E. 2013 Continuum theory of phase separation kinetics for active Brownian particles. Phys. Rev. Lett. 111 (14), 145702.CrossRefGoogle ScholarPubMed
Stone, H.A. & Samuel, A.D.T. 1996 Propulsion of microorganisms by surface distortions. Phys. Rev. Lett. 77, 4102.CrossRefGoogle ScholarPubMed
Swan, J.W., Brady, J.F., Moore, R.S. & ChE 174 2011 Modeling hydrodynamic self-propulsion with Stokesian dynamics or teaching Stokesian dynamics to swim. Phys. Fluids 23 (7), 71901.CrossRefGoogle Scholar
Tailleur, J. & Cates, M.E. 2008 Statistical mechanics of interacting run-and-tumble bacteria. Phys. Rev. Lett. 100 (21), 218103.CrossRefGoogle ScholarPubMed
Takatori, S.C. & Brady, J.F. 2014 Swim stress, motion, and deformation of active matter: effect of an external field. Soft Matt. 10 (47), 9433.CrossRefGoogle ScholarPubMed
Takatori, S.C. & Brady, J.F. 2015 Towards a thermodynamics of active matter. Phys. Rev. E 91, 032117.CrossRefGoogle ScholarPubMed
Takatori, S.C., De Dier, R., Vermant, J & Brady, J.F. 2016 Acoustic trapping of active matter. Nat. Commun. 7, 10694.CrossRefGoogle ScholarPubMed
Takatori, S.C., Yan, W. & Brady, J.F. 2014 Swim pressure: stress generation in active matter. Phys. Rev. Lett. 113 (2), 028103.CrossRefGoogle ScholarPubMed
Wysocki, A., Winkler, R.G. & Gompper, G. 2014 Cooperative motion of active Brownian spheres in three-dimensional dense suspensions. Europhys. Lett. 105 (4), 48004.CrossRefGoogle Scholar
Yan, W. & Brady, J.F. 2015 The force on a boundary in active matter. J. Fluid Mech. 785, R1.CrossRefGoogle Scholar
Yan, W. & Brady, J.F. 2018 The curved kinetic boundary layer of active matter. Soft Matt. 14 (2), 279–290.CrossRefGoogle ScholarPubMed