Published online by Cambridge University Press: 28 April 2016
In theoretical treatments of turbulent fountains, the entrainment of ambient fluid into the top of the fountain, hereinafter fountain-top entrainment 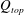 $Q_{top}$ (
$Q_{top}$ ( $\text{m}^{3}~\text{s}^{-1}$), has been neglected until now. This neglect, which modifies the energetic balance in a fountain, compromises the predictive ability of existing models. Our aim is to quantify
$\text{m}^{3}~\text{s}^{-1}$), has been neglected until now. This neglect, which modifies the energetic balance in a fountain, compromises the predictive ability of existing models. Our aim is to quantify 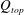 $Q_{top}$ by shedding light on the physical processes that are responsible for fountain-top entrainment. First, estimates for
$Q_{top}$ by shedding light on the physical processes that are responsible for fountain-top entrainment. First, estimates for  $Q_{top}$ are obtained by applying, in turn, an entrainment closure in the vein of Morton et al. (Proc. R. Soc. Lond., vol. 234, 1956, pp. 1–23) and then of Shrinivas & Hunt (J. Fluid Mech., vol. 757, 2014, pp. 573–598) to the time-averaged fountain top. Unravelling the assumptions that underlie these approaches, we argue that neither capture the dynamical behaviour of the flow observed at the fountain top; the top being characterised by quasi-periodic fluctuations, during which large-scale eddies reverse and engulf parcels of ambient fluid into the fountain. Therefore, shifting our mindset to a periodical framework, we develop a new phenomenological model in which we emphasise the role of the fluctuations in entraining external fluid. Our model suggests that
$Q_{top}$ are obtained by applying, in turn, an entrainment closure in the vein of Morton et al. (Proc. R. Soc. Lond., vol. 234, 1956, pp. 1–23) and then of Shrinivas & Hunt (J. Fluid Mech., vol. 757, 2014, pp. 573–598) to the time-averaged fountain top. Unravelling the assumptions that underlie these approaches, we argue that neither capture the dynamical behaviour of the flow observed at the fountain top; the top being characterised by quasi-periodic fluctuations, during which large-scale eddies reverse and engulf parcels of ambient fluid into the fountain. Therefore, shifting our mindset to a periodical framework, we develop a new phenomenological model in which we emphasise the role of the fluctuations in entraining external fluid. Our model suggests that 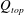 $Q_{top}$ is similar in magnitude to the volume flux supplied to the fountain top by the upflow (
$Q_{top}$ is similar in magnitude to the volume flux supplied to the fountain top by the upflow (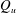 $Q_{u}$), i.e.
$Q_{u}$), i.e. 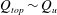 $Q_{top}\sim Q_{u}$, in agreement with experimental evidence. We conclude by providing guidance on how to implement fountain-top entrainment in existing models of turbulent fountains.
$Q_{top}\sim Q_{u}$, in agreement with experimental evidence. We conclude by providing guidance on how to implement fountain-top entrainment in existing models of turbulent fountains.