Article contents
Perturbing vortex packets in a turbulent boundary layer
Published online by Cambridge University Press: 29 April 2014
Abstract
A zero pressure gradient turbulent boundary layer of 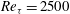 $\textit {Re}_{\tau }=2500$ was perturbed by a single spanwise array of finite cylinders mounted on the bounding surface and extending through the logarithmic region. The cylinder height was
$\textit {Re}_{\tau }=2500$ was perturbed by a single spanwise array of finite cylinders mounted on the bounding surface and extending through the logarithmic region. The cylinder height was 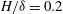 $H/\delta =0.2$ (
$H/\delta =0.2$ (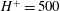 $H^{+}=500$), where
$H^{+}=500$), where 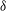 $\delta $ is the boundary layer thickness, with an aspect ratio (
$\delta $ is the boundary layer thickness, with an aspect ratio (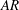 $AR$) (height/diameter) of four. Streamwise–spanwise (
$AR$) (height/diameter) of four. Streamwise–spanwise (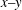 $x\text {--}y$) planes of the flow were examined by particle image velocimetry (PIV) up to
$x\text {--}y$) planes of the flow were examined by particle image velocimetry (PIV) up to 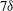 $7\delta $ downstream at a wall-normal location of
$7\delta $ downstream at a wall-normal location of 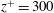 $z^{+}=300$ for cylinder array spacings ranging from
$z^{+}=300$ for cylinder array spacings ranging from 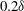 $0.2\delta $ to
$0.2\delta $ to 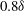 $0.8\delta $. Average streamwise velocity fields showed a splitting, then merging pattern of cylinder wakes which occurred further downstream as the cylinder spacing increased. Based on measurements at the furthest downstream location, both the spanwise variation of average streamwise velocity and the Fourier content in the instantaneous fields suggested that the case with
$0.8\delta $. Average streamwise velocity fields showed a splitting, then merging pattern of cylinder wakes which occurred further downstream as the cylinder spacing increased. Based on measurements at the furthest downstream location, both the spanwise variation of average streamwise velocity and the Fourier content in the instantaneous fields suggested that the case with 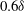 $0.6\delta $ cylinder spacing, which matched the dominant spanwise scale in the unperturbed flow, yielded the most persistent downstream flow organization. A flying PIV method was implemented to track specific packet structures over a range
$0.6\delta $ cylinder spacing, which matched the dominant spanwise scale in the unperturbed flow, yielded the most persistent downstream flow organization. A flying PIV method was implemented to track specific packet structures over a range 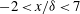 $-2<x/\delta <7$ with respect to the cylinder array, corresponding to a time scale of
$-2<x/\delta <7$ with respect to the cylinder array, corresponding to a time scale of 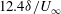 $12.4\delta /U_{\infty }$. Packets approaching the
$12.4\delta /U_{\infty }$. Packets approaching the 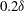 $0.2\delta $ spacing array first lost their organization but then regained it a distance
$0.2\delta $ spacing array first lost their organization but then regained it a distance 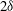 $2\delta $ downstream, suggesting that a persistent outer layer organization propagated inwards into the log region. For arrays with larger spanwise spacing, approaching packets were generally redirected into the spanwise location midway between cylinders and sometimes enhanced.
$2\delta $ downstream, suggesting that a persistent outer layer organization propagated inwards into the log region. For arrays with larger spanwise spacing, approaching packets were generally redirected into the spanwise location midway between cylinders and sometimes enhanced.
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 14
- Cited by


