Hostname: page-component-5cf477f64f-tx7qf Total loading time: 0 Render date: 2025-04-03T11:25:07.110Z Has data issue: false hasContentIssue false
  • English
  • Français

Penetrative turbulent Rayleigh–Bénard convection in two and three dimensions

Published online by Cambridge University Press:  14 May 2019

Qi Wang Open the ORCID record for Qi Wang [Opens in a new window] ,
Quan Zhou Open the ORCID record for Quan Zhou [Opens in a new window] ,
Zhen-Hua Wan Open the ORCID record for Zhen-Hua Wan [Opens in a new window]  and
De-Jun Sun
Qi Wang
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230027, China
Quan Zhou
Affiliation:
Shanghai Institute of Applied Mathematics and Mechanics, Shanghai University, Shanghai 200072, China
Zhen-Hua Wan*
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230027, China
De-Jun Sun*
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230027, China
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

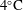Penetrative turbulent Rayleigh–Bénard convection which depends on the density maximum of water near $4^{\circ }\text{C}$ is studied using two-dimensional and three-dimensional direct numerical simulations. The working fluid is water near 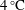$4\,^{\circ }\text{C}$ with Prandtl number 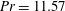$Pr=11.57$. The considered Rayleigh numbers 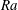$Ra$ range from 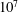$10^{7}$ to 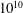$10^{10}$. The density inversion parameter 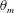$\unicode[STIX]{x1D703}_{m}$ varies from 0 to 0.9. It is found that the ratio of the top and bottom thermal boundary-layer thicknesses (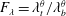$F_{\unicode[STIX]{x1D706}}=\unicode[STIX]{x1D706}_{t}^{\unicode[STIX]{x1D703}}/\unicode[STIX]{x1D706}_{b}^{\unicode[STIX]{x1D703}}$) increases with increasing 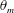$\unicode[STIX]{x1D703}_{m}$, and the relationship between 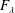$F_{\unicode[STIX]{x1D706}}$ and $\unicode[STIX]{x1D703}_{m}$ seems to be independent of 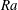$Ra$. The centre temperature 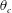$\unicode[STIX]{x1D703}_{c}$ is enhanced compared to that of Oberbeck–Boussinesq cases, as 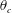$\unicode[STIX]{x1D703}_{c}$ is related to 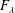$F_{\unicode[STIX]{x1D706}}$ with 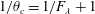$1/\unicode[STIX]{x1D703}_{c}=1/F_{\unicode[STIX]{x1D706}}+1$, 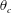$\unicode[STIX]{x1D703}_{c}$ is also found to have a universal relationship with $\unicode[STIX]{x1D703}_{m}$ which is independent of 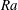$Ra$. Both the Nusselt number 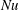$Nu$ and the Reynolds number 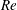$Re$ decrease with increasing 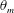$\unicode[STIX]{x1D703}_{m}$, the normalized Nusselt number 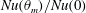$Nu(\unicode[STIX]{x1D703}_{m})/Nu(0)$ and Reynolds number 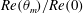$Re(\unicode[STIX]{x1D703}_{m})/Re(0)$ also have universal relationships with 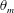$\unicode[STIX]{x1D703}_{m}$ which seem to be independent of both 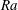$Ra$ and the aspect ratio 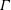$\unicode[STIX]{x1D6E4}$. The scaling exponents of $Nu\sim Ra^{\unicode[STIX]{x1D6FC}}$ and 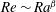$Re\sim Ra^{\unicode[STIX]{x1D6FD}}$ are found to be insensitive to 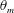$\unicode[STIX]{x1D703}_{m}$ despite of the remarkable change of the flow organizations.

JFM classification

Convection: Convection in cavities
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 870 , 10 July 2019 , pp. 718 - 734
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Araujo, F. F., Funfschilling, D., Grossmann, S. & Lohse, D. 2007 Non-Oberbeck-Boussinesq effects in gaseous Rayleigh–Bénard convection. Phys. Rev. Lett. 98 (5), 054501.Google Scholar
Ahlers, G., Brown, E., Araujo, F. F., Funfschilling, D., Grossmann, S. & Lohse, D. 2006 Non-Oberbeck–Boussinesq effects in strongly turbulent Rayleigh–Bénard convection. J. Fluid Mech. 569, 409–445.Google Scholar
Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.Google Scholar
Antar, B. N. 1987 Penetrative double-diffusive convection. Phys. Fluids 30 (2), 322–330.Google Scholar
Buffett, B. 2014 Geomagnetic fluctuations reveal stable stratification at the top of the Earth’s core. Nature 507 (7493), 484–487.Google Scholar
Chillà, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35 (7), 58.Google Scholar
Chong, K. L., Huang, S.-D., Kaczorowski, M. & Xia, K.-Q. 2015 Condensation of coherent structures in turbulent flows. Phys. Rev. Lett. 115 (26), 264503.Google Scholar
Chong, K. L., Wagner, S., Kaczorowski, M., Shishkina, O. & Xia, K.-Q. 2018 Effect of Prandtl number on heat transport enhancement in Rayleigh–Bénard convection under geometrical confinement. Phys. Rev. Fluid 3 (1), 013501.Google Scholar
Chong, K. L. & Xia, K.-Q. 2016 Exploring the severely confined regime in Rayleigh–Bénard convection. J. Fluid Mech. 805, R4.Google Scholar
Chong, K. L., Yang, Y.-T., Huang, S.-D., Zhong, J.-Q., Stevens, R. J. A. M., Verzicco, R., Lohse, D. & Xia, K.-Q. 2017 Confined Rayleigh–Bénard, Rotating Rayleigh–Bénard, and double diffusive convection: a unifying view on turbulent transport enhancement through coherent structure manipulation. Phys. Rev. Lett. 119 (6), 064501.Google Scholar
Couston, L.-A., Lecoanet, D., Favier, B. & Le Bars, M. 2018 Order out of chaos: slowly reversing mean flows emerge from turbulently generated internal waves. Phys. Rev. Lett. 120 (24), 244505.Google Scholar
Dintrans, B., Brandenburg, A., Nordlund, Å & Stein, R. F. 2005 Spectrum and amplitudes of internal gravity waves excited by penetrative convection in solar-type stars. Astron. Astrophys. 438 (1), 365–376.Google Scholar
Gebhart, B. & Mollendorf, J. C. 1977 A new density relation for pure and saline water. Deep-Sea Res. 24 (9), 831–848.Google Scholar
Goluskin, D. & van der Poel, E. P. 2016 Penetrative internally heated convection in two and three dimensions. J. Fluid Mech. 791, R6.Google Scholar
Horn, S. & Shishkina, O. 2014 Rotating non-Oberbeck–Boussinesq Rayleigh–Bénard convection in water. Phys. Fluids 26 (5), 055111.Google Scholar
Horn, S., Shishkina, O. & Wagner, C. 2013 On non-Oberbeck–Boussinesq effects in three-dimensional Rayleigh–Bénard convection in glycerol. J. Fluid Mech. 724, 175–202.Google Scholar
Hu, Y.-P., Li, Y.-R. & Wu, C.-M. 2015 Rayleigh–Bénard convection of cold water near its density maximum in a cubical cavity. Phys. Fluids 27 (3), 034102.Google Scholar
Huang, S.-D., Kaczorowski, M., Ni, R. & Xia, K.-Q. 2013 Confinement-induced heat-transport enhancement in turbulent thermal convection. Phys. Rev. Lett. 111 (10), 104501.Google Scholar
Huang, Y.-X. & Zhou, Q. 2013 Counter-gradient heat transport in two-dimensional turbulent Rayleigh–Bénard convection. J. Fluid Mech. 737, R3.Google Scholar
Johnston, H. & Doering, C. R. 2009 Comparison of turbulent thermal convection between conditions of constant temperature and constant flux. Phys. Rev. Lett. 102 (6), 064501.Google Scholar
Kong, D., Zhang, K., Schubert, G. & Anderson, J. D. 2018 Origin of jupiters cloud-level zonal winds remains a puzzle even after juno. Proc. Natl Acad. Sci. USA 115 (34), 8499–8504.Google Scholar
Large, E. & Andereck, C. D. 2014 Penetrative Rayleigh–Bénard convection in water near its maximum density point. Phys. Fluids 26 (9), 094101.Google Scholar
Lecoanet, D., Le Bars, M., Burns, K. J., Vasil, G. M., Brown, B. P., Quataert, E. & Oishi, J. S. 2015 Numerical simulations of internal wave generation by convection in water. Phys. Rev. E 91 (6), 063016.Google Scholar
Leighton, R. B. 1963 The solar granulation. Annu. Rev. Astron. Astrophys. 1 (1), 19–40.Google Scholar
Liu, S., Xia, S.-N., Yan, R., Wan, Z.-H. & Sun, D.-J. 2018 Linear and weakly nonlinear analysis of Rayleigh–Bénard convection of perfect gas with non-Oberbeck–Boussinesq effects. J. Fluid Mech. 845, 141–169.Google Scholar
Lohse, D. & Xia, K.-Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.Google Scholar
Moore, D. R. & Weiss, N. O. 1973 Nonlinear penetrative convection. J. Fluid Mech. 61 (3), 553–581.Google Scholar
Musman, S. 1968 Penetrative convection. J. Fluid Mech. 31 (2), 343–360.Google Scholar
Ostilla-Mónico, R., van der Poel, E. P., Verzicco, R., Grossmann, S. & Lohse, D. 2014 Exploring the phase diagram of fully turbulent Taylor–Couette flow. J. Fluid Mech. 761, 1–26.Google Scholar
Ostilla-Mónico, R., Stevens, R. J. A. M., Grossmann, S., Verzicco, R. & Lohse, D. 2013 Optimal Taylor–Couette flow: direct numerical simulations. J. Fluid Mech. 719, 14–46.Google Scholar
Sameen, A., Verzicco, R. & Sreenivasan, K. R. 2008 Non-Boussinesq convection at moderate Rayleigh numbers in low temperature gaseous helium. Phys. Scr. 2008 (T132), 014053.Google Scholar
Sameen, A., Verzicco, R. & Sreenivasan, K. R. 2009 Specific roles of fluid properties in non-Boussinesq thermal convection at the Rayleigh number of 2 × 108 . Eur. Phys. Lett. 86 (1), 14006.Google Scholar
Shishkina, O., Stevens, R. J. A. M., Grossmann, S. & Lohse, D. 2010 Boundary layer structure in turbulent thermal convection and its consequences for the required numerical resolution. New J. Phys. 12 (7), 075022.Google Scholar
Sugiyama, K., Calzavarini, E., Grossmann, S. & Lohse, D. 2009 Flow organization in two-dimensional non-Oberbeck–Boussinesq Rayleigh–Bénard convection in water. J. Fluid Mech. 637, 105–135.Google Scholar
Sugiyama, K., Ni, R., Stevens, R. J. A. M., Chan, T. S., Zhou, S.-Q., Xi, H.-D., Sun, C., Grossmann, S., Xia, K.-Q. & Lohse, D. 2010 Flow reversals in thermally driven turbulence. Phys. Rev. Lett. 105 (3), 034503.Google Scholar
Toppaladoddi, S. & Wettlaufer, J. S. 2018 Penetrative convection at high Rayleigh numbers. Phys. Rev. Fluid 3 (4), 043501.Google Scholar
Van Gils, D. P. M., Huisman, S. G., Bruggert, G.-W., Sun, C. & Lohse, D. 2011 Torque scaling in turbulent Taylor–Couette flow with co-and counterrotating cylinders. Phys. Rev. Lett. 106 (2), 024502.Google Scholar
Veronis, G. 1963 Penetrative convection. Astrophys. J. 137, 641–663.Google Scholar
Wang, Q., Wan, Z.-H., Yan, R. & Sun, D.-J. 2018a Multiple states and heat transfer in two-dimensional tilted convection with large aspect ratios. Phys. Rev. Fluid 3 (11), 113503.Google Scholar
Wang, Q., Wan, Z.-H., Yan, R. & Sun, D.-J. 2019a Flow organization and heat transfer in two-dimensional tilted convection with aspect ratio 0.5. Phys. Fluids 31 (2), 025102.Google Scholar
Wang, Q., Xia, S.-N., Wang, B.-F., Sun, D.-J., Zhou, Q. & Wan, Z.-H. 2018b Flow reversals in two-dimensional thermal convection in tilted cells. J. Fluid Mech. 849, 355–372.Google Scholar
Wang, Q., Xia, S.-N., Yan, R., Sun, D.-J. & Wan, Z.-H. 2019b Non-Oberbeck-Boussinesq effects due to large temperature differences in a differentially heated square cavity filled with air. Intl J. Heat Mass Transfer 128, 479–491.Google Scholar
Wang, Q., Xu, B.-L., Xia, S.-N., Wan, Z.-H. & Sun, D.-J. 2017 Thermal convection in a tilted rectangular cell with aspect ratio 0.5. Chin. Phys. Lett. 34 (10), 104401.Google Scholar
Weiss, S., He, X., Ahlers, G., Bodenschatz, E. & Shishkina, O. 2018 Bulk temperature and heat transport in turbulent Rayleigh–Bénard convection of fluids with temperature-dependent properties. J. Fluid Mech. 851, 374–390.Google Scholar
Xia, S.-N., Wan, Z.-H., Liu, S., Wang, Q. & Sun, D.-J. 2016 Flow reversals in Rayleigh–Bénard convection with non-Oberbeck–Boussinesq effects. J. Fluid Mech. 798, 628–642.Google Scholar
Zhang, J., Childress, S. & Libchaber, A. 1997 Non-Boussinesq effect: thermal convection with broken symmetry. Phys. Fluids 9 (4), 1034–1042.Google Scholar
Zhang, K. K. & Schubert, G. 1996 Penetrative convection and zonal flow on jupiter. Science 273 (5277), 941–943.Google Scholar
Zhang, K. K. & Schubert, G. 2000 Teleconvection: remotely driven thermal convection in rotating stratified spherical layers. Science 290 (5498), 1944–1947.Google Scholar
Zhang, Y., Zhou, Q. & Sun, C. 2017 Statistics of kinetic and thermal energy dissipation rates in two-dimensional turbulent Rayleigh–Bénard convection. J. Fluid Mech. 814, 165–184.Google Scholar