Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-23T14:30:25.587Z Has data issue: false hasContentIssue false
  • English
  • Français

The other optimal Stokes drag profile

Published online by Cambridge University Press:  27 November 2014

Thomas D. Montenegro-Johnson  and
Eric Lauga
Thomas D. Montenegro-Johnson
Affiliation:
Department of Applied Mathematics and Theoretical Physics, Centre for Mathematical Sciences, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
Eric Lauga*
Affiliation:
Department of Applied Mathematics and Theoretical Physics, Centre for Mathematical Sciences, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The lowest drag shape of fixed volume in Stokes flow has been known for some 40 years. It is front–back symmetric and similar to an American football with ends tangent to a cone of 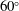$60^{\circ }$. The analogous convex axisymmetric shape of fixed surface area, which may be of interest for particle design in chemistry and colloidal science, is characterised in this paper. This ‘other’ optimal shape has a surface vorticity proportional to the mean surface curvature, which is used with a local analysis of the flow near the tip to show that the front and rear ends are tangent to a cone of angle 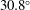$30.8^{\circ }$. Using the boundary element method, we numerically represent the shape by expanding its tangent angle in terms decaying odd Legendre modes, and show that it has 11.3 % lower drag than a sphere of equal surface area, significantly more pronounced than for the fixed-volume optimal.

JFM classification

Low-Reynolds-number flows: Boundary integral methods Flow Control: Drag reduction Low-Reynolds-number flows: Low-Reynolds-number flows
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 762 , 10 January 2015 , R3
Check for updates
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alonso, J. J., LeGresley, P. & Pereyra, V. 2009 Aircraft design optimization. Math. Comput. Simul. 79 (6), 1948–1958.Google Scholar
Bourot, J.-M. 1974 On the numerical computation of the optimum profile in Stokes flow. J. Fluid Mech. 65 (03), 513–515.Google Scholar
Campana, E. F., Liuzzi, G., Lucidi, S., Peri, D., Piccialli, V. & Pinto, A. 2009 New global optimization methods for ship design problems. Optim. Eng. 10 (4), 533–555.CrossRefGoogle Scholar
Champion, J. A., Katare, Y. K. & Mitragotri, S. 2007 Particle shape: a new design parameter for micro- and nanoscale drug delivery carriers. J. Cont. Rel. 121 (1), 3–9.CrossRefGoogle ScholarPubMed
Champion, J. A. & Mitragotri, S. 2006 Role of target geometry in phagocytosis. Proc. Natl Acad. Sci. USA 103 (13), 4930–4934.Google Scholar
Chwang, A.T. & Wu, T. 1975 Hydromechanics of low-Reynolds-number flow. Part 2. Singularity method for Stokes flows. J. Fluid Mech. 67 (4), 787–815.CrossRefGoogle Scholar
Eloy, C. & Lauga, E. 2012 Kinematics of the most efficient cilium. Phys. Rev. Lett. 109, 038101.Google Scholar
Gratton, S. E. A., Ropp, P. A., Pohlhaus, P. D., Luft, J. C., Madden, V. J., Napier, M. E. & DeSimone, J. M. 2008 The effect of particle design on cellular internalization pathways. Proc. Natl Acad. Sci. USA 105 (33), 11613–11618.CrossRefGoogle ScholarPubMed
Jameson, A., Martinelli, L. & Pierce, N. A. 1998 Optimum aerodynamic design using the Navier–Stokes equations. Theor. Comput. Fluid Dyn. 10 (1–4), 213–237.CrossRefGoogle Scholar
Keaveny, E. E., Walker, S. W. & Shelley, M. J. 2013 Optimization of chiral structures for microscale propulsion. Nano Lett. 13 (2), 531–537.CrossRefGoogle ScholarPubMed
Lauga, E. & Eloy, C. 2013 Shape of optimal active flagella. J. Fluid Mech. 730, R1.Google Scholar
Mitragotri, S. & Lahann, J. 2009 Physical approaches to biomaterial design. Nat. Mater. 8 (1), 15–23.Google Scholar
Mohammadi, B. & Pironneau, O. 2004 Shape optimization in fluid mechanics. Annu. Rev. Fluid Mech. 36, 255–279.Google Scholar
Monteiller, C., Tran, L., MacNee, W., Faux, S., Jones, A., Miller, B. & Donaldson, K. 2007 The pro-inflammatory effects of low-toxicity low-solubility particles, nanoparticles and fine particles, on epithelial cells in vitro: the role of surface area. Occupat. Environ. Med. 64 (9), 609–615.Google Scholar
Osterman, N & Vilfan, A. 2011 Finding the ciliary beating pattern with optimal efficiency. Proc. Natl Acad. Sci. USA 108 (38), 15727–15732.Google Scholar
Petros, R. A. & DeSimone, J. M. 2010 Strategies in the design of nanoparticles for therapeutic applications. Nat. Rev. Drug Disc. 9 (8), 615–627.CrossRefGoogle ScholarPubMed
Pironneau, O. 1973 On optimum profiles in Stokes flow. J. Fluid Mech. 59 (1), 117–128.Google Scholar
Pironneau, O. & Katz, D. F. 1974 Optimal swimming of flagellated micro-organisms. J. Fluid Mech. 66 (02), 391–415.Google Scholar
Pozrikidis, C. 1992 Boundary Integral and Singularity Methods for Linearized Viscous Flow. Cambridge University Press.Google Scholar
Pozrikidis, C. 2002 A Practical Guide to Boundary Element Methods with the Software Library BEMLIB. Taylor & Francis.CrossRefGoogle Scholar
Roper, M., Pepper, R. E., Brenner, M. P. & Pringle, A. 2008 Explosively launched spores of ascomycete fungi have drag-minimizing shapes. Proc. Natl Acad. Sci. USA 105 (52), 20583–20588.Google Scholar
Vilfan, A. 2012 Optimal shapes of surface slip driven self-propelled microswimmers. Phys. Rev. Lett. 109, 128105.Google Scholar
Wakiya, S. 1976 Axisymmetric flow of a viscous fluid near the vertex of a body. J. Fluid Mech. 78 (4), 737–747.Google Scholar
Zabarankin, M. 2013 Minimum-resistance shapes in linear continuum mechanics. Proc. R. Soc. Lond. A 469 (2160), 0206.Google Scholar