Published online by Cambridge University Press: 04 April 2018
Oscillatory flow around a circular cylinder close to a plane boundary is numerically investigated at low-to-intermediate Keulegan–Carpenter (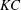 $KC$) and Stokes numbers (
$KC$) and Stokes numbers (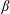 $\unicode[STIX]{x1D6FD}$) for different gap-to-diameter ratios (
$\unicode[STIX]{x1D6FD}$) for different gap-to-diameter ratios (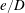 $e/D$). A set of unique flow regimes is observed and classified based on the established nomenclature in the (
$e/D$). A set of unique flow regimes is observed and classified based on the established nomenclature in the (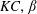 $KC,\unicode[STIX]{x1D6FD}$)-space. It is found that the flow is not only influenced by
$KC,\unicode[STIX]{x1D6FD}$)-space. It is found that the flow is not only influenced by 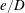 $e/D$ but also by the ratio of the thickness of the Stokes boundary layer (
$e/D$ but also by the ratio of the thickness of the Stokes boundary layer (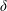 $\unicode[STIX]{x1D6FF}$) to the gap size (e). At relatively large
$\unicode[STIX]{x1D6FF}$) to the gap size (e). At relatively large 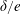 $\unicode[STIX]{x1D6FF}/e$ values, vortex shedding through the gap is suppressed and vortices are only shed from the top of the cylinder. At intermediate values of
$\unicode[STIX]{x1D6FF}/e$ values, vortex shedding through the gap is suppressed and vortices are only shed from the top of the cylinder. At intermediate values of  $\unicode[STIX]{x1D6FF}/e$, flow through the gap is enhanced, resulting in horizontal gap vortex shedding. As
$\unicode[STIX]{x1D6FF}/e$, flow through the gap is enhanced, resulting in horizontal gap vortex shedding. As 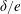 $\unicode[STIX]{x1D6FF}/e$ is further reduced below a critical value, the influence of
$\unicode[STIX]{x1D6FF}/e$ is further reduced below a critical value, the influence of 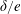 $\unicode[STIX]{x1D6FF}/e$ becomes negligible and the flow is largely dependent on
$\unicode[STIX]{x1D6FF}/e$ becomes negligible and the flow is largely dependent on 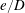 $e/D$. A hysteresis phenomenon is observed for the transitions in the flow regime. The physical mechanisms responsible for the hysteresis and the variation of marginal stability curves with
$e/D$. A hysteresis phenomenon is observed for the transitions in the flow regime. The physical mechanisms responsible for the hysteresis and the variation of marginal stability curves with 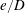 $e/D$ are explored at
$e/D$ are explored at  $KC=6$ through specifically designed numerical simulations. The Stokes boundary layer over the plane boundary is found to be responsible for the relatively large hysteresis range over
$KC=6$ through specifically designed numerical simulations. The Stokes boundary layer over the plane boundary is found to be responsible for the relatively large hysteresis range over 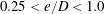 $0.25<e/D<1.0$. Three mechanisms have been identified to the change of the marginal stability curve over
$0.25<e/D<1.0$. Three mechanisms have been identified to the change of the marginal stability curve over 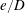 $e/D$, which are the blockage effect due to the geometry setting, the favourable pressure gradient over the gap and the location of the leading eigenmode relative to the cylinder.
$e/D$, which are the blockage effect due to the geometry setting, the favourable pressure gradient over the gap and the location of the leading eigenmode relative to the cylinder.
Animation of streakline in regime HA at (e/D, KC, β)=(0.25,10, 10).
Animation of streakline in regime GVS at (e/D, KC, β)=(0.5, 6, 20).
Animation of streakline in regime GVS-A at (e/D, KC, β)=(0.5, 6, 30).