Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T23:44:56.809Z Has data issue: false hasContentIssue false
  • English
  • Français

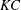Oscillatory flow regimes around four cylinders in a square arrangement under small $\mathit{KC}$ and 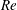$\mathit{Re}$ conditions

Published online by Cambridge University Press:  17 March 2015

Feifei Tong ,
Liang Cheng ,
Ming Zhao  and
Hongwei An
Feifei Tong*
Affiliation:
School of Civil, Environmental and Mining Engineering, University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia
Liang Cheng
Affiliation:
School of Civil, Environmental and Mining Engineering, University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, PR China
Ming Zhao
Affiliation:
School of Computing, Engineering and Mathematics, University of Western Sydney, Locked Bag 1797, Penrith, NSW 2751, Australia
Hongwei An
Affiliation:
School of Civil, Environmental and Mining Engineering, University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

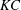Sinusoidally oscillatory flow around four circular cylinders in an in-line square arrangement is numerically investigated at Keulegan–Carpenter numbers ($\mathit{KC}$) ranging from 1 to 12 and at Reynolds numbers (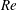$\mathit{Re}$) from 20 to 200. A set of flow patterns is observed and classified based on known oscillatory flow regimes around a single cylinder. These include six types of reflection symmetry regimes to the axis of flow oscillation, two types of spatio-temporal symmetry regimes and a series of symmetry-breaking flow patterns. In general, at small gap distances, the four structures behave more like a single body, and the flow fields therefore resemble those around a single cylinder with a large effective cylinder diameter. With increasing gap distance, flow structures around each individual cylinder in the array start to influence the overall flow patterns, and the flow field shows a variety of symmetry and asymmetry patterns as a result of vortex and shear layer interactions. The characteristics of hydrodynamic forces on individual cylinders as well as on the cylinder group are also examined. It is found that the hydrodynamic forces respond in a similar manner to the flow field to the cylinder proximity and wake interference.

JFM classification

Low-Reynolds-number flows: Low-Reynolds-number flows Vortex Flows: Vortex Flows Vortex Flows: Vortex interactions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 769 , 25 April 2015 , pp. 298 - 336
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

An, H., Cheng, L. & Zhao, M. 2011 Direct numerical simulation of oscillatory flow around a circular cylinder at low Keulegan–Carpenter number. J. Fluid Mech. 666, 77–103.CrossRefGoogle Scholar
Anagnostopoulos, P. & Dikarou, C. 2011 Numerical simulation of viscous oscillatory flow past four cylinders in square arrangement. J. Fluids Struct. 27, 212–232.CrossRefGoogle Scholar
Anagnostopoulos, P. & Minear, R. 2004 Blockage effect of oscillatory flow past a fixed cylinder. Appl. Ocean Res. 26, 147–153.CrossRefGoogle Scholar
Bearman, P. W. 1984 Vortex shedding from oscillating bluff bodies. Annu. Rev. Fluid Mech. 16, 195–222.CrossRefGoogle Scholar
Bearman, P., Downie, M., Graham, J. & Obasaju, E. 1985 Forces on cylinders in viscous oscillatory flow at low Keulegan–Carpenter numbers. J. Fluid Mech. 154, 337–356.CrossRefGoogle Scholar
Carmo, B. S., Meneghini, J. R. & Sherwin, S. J. 2010 Secondary instabilities in the flow around two circular cylinders in tandem. J. Fluid Mech. 644, 395–431.CrossRefGoogle Scholar
Chern, M.-J., Rajesh Kanna, P., Lu, Y.-J., Cheng, I. & Chang, S.-C. 2010 A CFD study of the interaction of oscillatory flows with a pair of side-by-side cylinders. J. Fluids Struct. 26, 626–643.CrossRefGoogle Scholar
Chern, M.-J., Shiu, W.-C. & Horng, T.-L. 2013 Immersed boundary modeling for interaction of oscillatory flow with cylinder array under effects of flow direction and cylinder arrangement. J. Fluids Struct. 43, 325–346.CrossRefGoogle Scholar
Dütsch, H., Durst, F., Becker, S. & Lienhart, H. 1998 Low-Reynolds-number flow around an oscillating circular cylinder at low Keulegan–Carpenter numbers. J. Fluid Mech. 360, 249–271.CrossRefGoogle Scholar
Elston, J. R., Blackburn, H. M. & Sheridan, J. 2006 The primary and secondary instabilities of flow generated by an oscillating circular cylinder. J. Fluid Mech. 550, 359–389.CrossRefGoogle Scholar
Elston, J. R., Sheridan, J. & Blackburn, H. M. 2004 Two-dimensional Floquet stability analysis of the flow produced by an oscillating circular cylinder in quiescent fluid. Eur. J. Mech. (B/ Fluids) 23, 99–106.CrossRefGoogle Scholar
Hall, P. 1984 On the stability of the unsteady boundary layer on a cylinder oscillating transversely in a viscous fluid. J. Fluid Mech. 146, 347–367.CrossRefGoogle Scholar
Honji, H. 1981 Streaked flow around an oscillating circular cylinder. J. Fluid Mech. 107, 509–520.CrossRefGoogle Scholar
Hu, J. & Zhou, Y. 2008 Flow structure behind two staggered circular cylinders. Part 1. Downstream evolution and classification. J. Fluid Mech. 607, 51–80.CrossRefGoogle Scholar
Iliadis, G. & Anagnostopoulos, P. 1998 Viscous oscillatory flow around a circular cylinder at low Keulegan–Carpenter numbers and frequency parameters. Intl J. Numer. Meth. Fluids 26, 403–442.3.0.CO;2-V>CrossRefGoogle Scholar
Justesen, P. 1991 A numerical study of oscillating flow around a circular cylinder. J. Fluid Mech. 222, 157–196.CrossRefGoogle Scholar
Kuehtz, S.1996 Experimental investigation of oscillatory flow around circular cylinders at low ${\it\beta}$ numbers. PhD thesis, Imperial College London.Google Scholar
Lin, X. W., Bearman, P. W. & Graham, J. M. R. 1996 A numerical study of oscillatory flow about a circular cylinder for low values of beta parameter. J. Fluids Struct. 10, 501–526.CrossRefGoogle Scholar
Maull, D. & Milliner, M. 1978 Sinusoidal flow past a circular cylinder. Coast. Engng 2, 149–168.CrossRefGoogle Scholar
Morison, J., Johnson, J. & Schaaf, S. 1950 The force exerted by surface waves on piles. J. Petrol. Tech. 2, 149–154.CrossRefGoogle Scholar
Nehari, D., Armenio, V. & Ballio, F. 2004 Three-dimensional analysis of the unidirectional oscillatory flow around a circular cylinder at low Keulegan–Carpenter and beta numbers. J. Fluid Mech. 520, 157–186.CrossRefGoogle Scholar
Obasaju, E., Bearman, P. & Graham, J. 1988 A study of forces, circulation and vortex patterns around a circular cylinder in oscillating flow. J. Fluid Mech. 196, 467–494.CrossRefGoogle Scholar
Papaioannou, G. V., Yue, D. K. P., Triantafyllou, M. S. & Karniadakis, G. E. 2006 Three-dimensionality effects in flow around two tandem cylinders. J. Fluid Mech. 558, 387–413.CrossRefGoogle Scholar
Saghafian, M., Stansby, P., Saidi, M. & Apsley, D. 2003 Simulation of turbulent flows around a circular cylinder using nonlinear eddy-viscosity modelling: steady and oscillatory ambient flows. J. Fluids Struct. 17, 1213–1236.CrossRefGoogle Scholar
Sarpkaya, T. 2002 Experiments on the stability of sinusoidal flow over a circular cylinder. J. Fluid Mech. 457, 157–180.CrossRefGoogle Scholar
Scandura, P., Armenio, V. & Foti, E. 2009 Numerical investigation of the oscillatory flow around a circular cylinder close to a wall at moderate Keulegan–Carpenter and low Reynolds numbers. J. Fluid Mech. 627, 259–290.CrossRefGoogle Scholar
Tatsuno, M. & Bearman, P. 1990 A visual study of the flow around an oscillating circular cylinder at low Keulegan–Carpenter numbers and low Stokes numbers. J. Fluid Mech. 211, 157–182.CrossRefGoogle Scholar
Uzunoğlu, B., Tan, M. & Price, W. 2001 Low-Reynolds-number flow around an oscillating circular cylinder using a cell viscous boundary element method. Intl J. Numer. Meth. Engng 50, 2317–2338.CrossRefGoogle Scholar
Williamson, C. H. K. 1985 Sinusoidal flow relative to circular cylinders. J. Fluid Mech. 155, 141–174.CrossRefGoogle Scholar
Yang, K., Cheng, L., An, H., Bassom, A. P. & Zhao, M. 2013 The effect of a piggyback cylinder on the flow characteristics in oscillatory flow. Ocean Engng 62, 45–55.CrossRefGoogle Scholar
Zdravkovich, M. M. 1987 The effects of interference between circular cylinders in cross flow. J. Fluids Struct. 1, 239–261.CrossRefGoogle Scholar
Zhao, M. & Cheng, L. 2014 Vortex shedding regimes of oscillatory flow past two circular cylinders in side-by-side and tandem arrangements at low Reynolds number. J. Fluid Mech. 751, 1–137.CrossRefGoogle Scholar