Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T21:40:22.388Z Has data issue: false hasContentIssue false
  • English
  • Français

Oscillatory and streaming flow between two spheres due to combined oscillations

Published online by Cambridge University Press:  03 August 2017

Dejuan Kong Open the ORCID record for Dejuan Kong [Opens in a new window] ,
Anita Penkova  and
Satwindar Singh Sadhal
Dejuan Kong
Affiliation:
Department of Aerospace and Mechanical Engineering, University of Southern California, Los Angeles, CA 90089-1453, USA
Anita Penkova
Affiliation:
Department of Aerospace and Mechanical Engineering, University of Southern California, Los Angeles, CA 90089-1453, USA
Satwindar Singh Sadhal*
Affiliation:
Department of Aerospace and Mechanical Engineering, University of Southern California, Los Angeles, CA 90089-1453, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The flow induced by the combined torsional and transverse oscillations of a sphere with amplitude ratio $\unicode[STIX]{x1D6FC}$ and phase difference 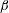$\unicode[STIX]{x1D6FD}$ in a concentric spherical container is examined. Analytical solutions of the leading-order flow field and shear stress profiles have been obtained. Steady streaming flows are also analysed not only for the case of unrestricted Womersley number 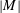$|M|$, but also in the low-frequency 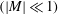$(|M|\ll 1)$ and high-frequency (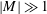$|M|\gg 1$) limits. At high frequency, the flow field has been divided into three regions: two boundary layers and the outer region. The streaming flow field is determined for the limiting case of the streaming Reynolds number 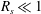$R_{s}\ll 1$. The results are compared with those of single torsional or transverse oscillation, and found to match very well. The amplitude ratio $\unicode[STIX]{x1D6FC}$ and phase difference 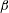$\unicode[STIX]{x1D6FD}$, in determining the streaming, are also discussed. The number and direction of steady streaming recirculation on the $r$–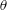$\unicode[STIX]{x1D703}$ plane depend on value of the amplitude ratio $\unicode[STIX]{x1D6FC}$. The phase difference 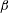$\unicode[STIX]{x1D6FD}$ plays a dominant role in the azimuthal velocity 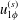$u_{1\unicode[STIX]{x1D719}}^{(s)}$ of steady streaming. When 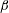$\unicode[STIX]{x1D6FD}$ is approximately 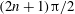$(2n+1)\unicode[STIX]{x03C0}/2$, 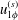$u_{1\unicode[STIX]{x1D719}}^{(s)}$ vanishes under low-frequency oscillation, while steady streaming has a recirculation on the $r$–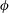$\unicode[STIX]{x1D719}$ plane under higher-frequency oscillation.

JFM classification

Acoustics: Acoustics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 826 , 10 September 2017 , pp. 335 - 362
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aldridge, K. D. & Toomre, A. 1969 Axisymmetric inertial oscillations of a fluid in a rotating spherical container. J. Fluid Mech. 37 (02), 307–323.CrossRefGoogle Scholar
Amin, N. & Riley, N. 1990 Streaming from a sphere due to a pulsating source. J. Fluid Mech. 210, 459–473.CrossRefGoogle Scholar
Bonfiglio, A., Repetto, R., Siggers, J. H. & Stocchino, A. 2013 Investigation of the motion of a viscous fluid in the vitreous cavity induced by eye rotations and implications for drug delivery. Phys. Med. Biol. 58 (6), 1969–1982.CrossRefGoogle ScholarPubMed
Bruus, H. 2012 Acoustofluidics 2: perturbation theory and ultrasound resonance modes. Lab on a Chip 12 (1), 20–28.Google Scholar
Bruus, H. 2014 Perturbation theory and ultrasound resonances. In Microscale Acoustofluidics (ed. Laurell, T. & Lenshof, A.), pp. 29–45. Royal Society of Chemistry.Google Scholar
Busse, F. H. 2010 Mean zonal flows generated by librations of a rotating spherical cavity. J. Fluid Mech. 650, 505–512.CrossRefGoogle Scholar
Calkins, M. A., Noir, J., Eldredge, J. D. & Aurnou, J. M. 2010 Axisymmetric simulations of libration-driven fluid dynamics in a spherical shell geometry. Phys. Fluids 22 (8), 086602.CrossRefGoogle Scholar
Dual, J., Hahn, P., Leibacher, I., Möller, D., Schwarz, T. & Wang, J. 2012 Acoustofluidics 19: ultrasonic microrobotics in cavities: devices and numerical simulation. Lab on a Chip 12 (20), 4010–4021.Google Scholar
Gopinath, A.1992 Convective heat transfer in acoustic streaming flows. PhD thesis, University of California, Los Angeles.Google Scholar
Gopinath, A. 1993 Steady streaming due to small-amplitude torsional oscillations of a sphere in a viscous fluid. Q. J. Mech. Appl. Maths 46 (3), 501–520.CrossRefGoogle Scholar
Gopinath, A. 1994 Steady streaming due to small-amplitude superposed oscillations of a sphere in a viscous fluid. Q. J. Mech. Appl. Maths 47 (3), 461–480.Google Scholar
Green, R., Ohlin, M. & Wiklund, M. 2014 Applications of acoustic streaming. In Microscale Acoustofluidics (ed. Laurell, T. & Lenshof, A.), pp. 312–336. Royal Society of Chemistry.Google Scholar
Jia, K., Yang, K. & Mei, D. 2012 Quantitative trap and long range transportation of micro-particles by using phase controllable acoustic wave. J. Appl. Phys. 112 (5), 054908.Google Scholar
Kelly, R. E. 1966 Streaming effects associated with doubly oscillating cylinders. Q. J. Mech. Appl. Maths 19 (4), 473–484.CrossRefGoogle Scholar
Kida, S. 2011 Steady flow in a rapidly rotating sphere with weak precession. J. Fluid Mech. 680, 150–193.CrossRefGoogle Scholar
Koch, S., Harlander, U., Egbers, C. & Hollerbach, R. 2013 Inertial waves in a spherical shell induced by librations of the inner sphere: experimental and numerical results. Fluid Dyn. Res. 45 (3), 035504.Google Scholar
Kong, D., Penkova, A. & Sadhal, S. S. 2015 Oscillatory flow between two hemispheres for shearing protein solution. Trans. ASME J. Fluids Engng 137 (10), 101201.CrossRefGoogle Scholar
Lighthill, J. 1978 Acoustic streaming. J. Sound Vib. 61 (3), 391–418.Google Scholar
Longuet-Higgins, M. S. 1997 Particle drift near an oscillating bubble. In Proc. R. Soc. Lond. Series A: Math. Phys. Eng. Sci., vol. 453, pp. 1551–1568. The Royal Society.Google Scholar
Longuet-Higgins, M. S. 1998 Viscous streaming from an oscillating spherical bubble. In Proc. R. Soc. Lond. Series A: Math. Phys. Eng. Sci., vol. 454, pp. 725–742. The Royal Society.Google Scholar
Mei, R. 1994 Flow due to an oscillating sphere and an expression for unsteady drag on the sphere at finite Reynolds number. J. Fluid Mech. 270, 133–174.Google Scholar
Meskauskas, J., Repetto, R. & Siggers, J. H. 2011 Oscillatory motion of a viscoelastic fluid within a spherical cavity. J. Fluid Mech. 685, 1–22.Google Scholar
Muller, P. B., Rossi, M., Marín, Á. G., Barnkob, R., Augustsson, P., Laurell, T., Kaehler, C. J. & Bruus, H. 2013 Ultrasound-induced acoustophoretic motion of microparticles in three dimensions. Phys. Rev. E 88 (2), 023006.Google Scholar
Noir, J., Hemmerlin, F., Wicht, J., Baca, S. M. & Aurnou, J. M. 2009 An experimental and numerical study of librationally driven flow in planetary cores and subsurface oceans. Phys. Earth Planet. Inter. 173 (1), 141–152.Google Scholar
Nyborg, W. L. 1953 Acoustic streaming due to attenuated plane waves. J. Acoust. Soc. Am. 25 (1), 68–75.Google Scholar
Panagopoulos, A. A., Psillakis, Z. M. & Karahalios, G. T. 1991 Steady streaming induced by a cylinder performing transverse and torsional oscillations. Phys. Fluids A 3 (5), 782–792.Google Scholar
Rallabandi, B., Marin, A., Rossi, M., Kähler, C. J. & Hilgenfeldt, S. 2015 Three-dimensional streaming flow in confined geometries. J. Fluid Mech. 777, 408–429.Google Scholar
Rallabandi, B., Wang, C. & Hilgenfeldt, S. 2014 Two-dimensional streaming flows driven by sessile semicylindrical microbubbles. J. Fluid Mech. 739, 57–71.Google Scholar
Rayleigh, L. 1884 On the circulation of air observed in kundt’s tubes, and on some allied acoustical problems. Phil. Trans. R. Soc. Lond. A 175, 1–21.Google Scholar
Rednikov, A. Y., Riley, N. & Sadhal, S. S. 2003 The behaviour of a particle in orthogonal acoustic fields. J. Fluid Mech. 486, 1–20.Google Scholar
Rednikov, A. Y. & Sadhal, S. S. 2011 Acoustic/steady streaming from a motionless boundary and related phenomena: generalized treatment of the inner streaming and examples. J. Fluid Mech. 667, 426–462.Google Scholar
Rednikov, A. Y., Zhao, H., Sadhal, S. S. & Trinh, E. H. 2006 Steady streaming around a spherical drop displaced from the velocity antinode in an acoustic levitation field. Q. J. Mech. Appl. Maths 59 (3), 377–397.Google Scholar
Repetto, R., Siggers, J. H. & Meskauskas, J. 2014 Steady streaming of a viscoelastic fluid within a periodically rotating sphere. J. Fluid Mech. 761, 329–347.Google Scholar
Repetto, R., Siggers, J. H. & Stocchino, A. 2008 Steady streaming within a periodically rotating sphere. J. Fluid Mech. 608, 71–80.Google Scholar
Repetto, R., Siggers, J. H. & Stocchino, A. 2010 Mathematical model of flow in the vitreous humor induced by saccadic eye rotations: effect of geometry. Biomech. Model. Mechanobiol. 9 (1), 65–76.Google Scholar
Repetto, R., Stocchino, A. & Cafferata, C. 2005 Experimental investigation of vitreous humour motion within a human eye model. Phys. Med. Biol. 50 (19), 4729–4743.Google Scholar
Riley, N. 1966 On a sphere oscillating in a viscous fluid. Q. J. Mech. Appl. Maths 19 (4), 461–472.Google Scholar
Riley, N. 1991 Oscillating viscous flows: II superposed oscillations. Mathematika 38 (02), 203–216.Google Scholar
Riley, N. 1998 Acoustic streaming. Theor. Comput. Fluid Dyn. 10 (1–4), 349–356.CrossRefGoogle Scholar
Riley, N. 2001 Steady streaming. Annu. Rev. Fluid Mech. 33 (1), 43–65.CrossRefGoogle Scholar
Rosenblat, S. 1959 Torsional oscillations of a plane in a viscous fluid. J. Fluid Mech. 6 (02), 206–220.Google Scholar
Sadhal, S. S. 2012a Acoustofluidics 13: analysis of acoustic streaming by perturbation methods. Lab on a Chip 12 (13), 2292–2300.Google Scholar
Sadhal, S. S. 2012b Acoustofluidics 15: streaming with sound waves interacting with solid particles. Lab on a Chip 12 (15), 2600–2611.Google Scholar
Sadhal, S. S. 2012c Acoustofluidics 16: acoustics streaming near liquid–gas interfaces: drops and bubbles. Lab on a Chip 12 (16), 2771–2781.Google Scholar
Sadhal, S. S. 2014 Analysis of acoustic streaming by perturbation methods. In Microscale Acoustofluidics (ed. Laurell, T. & Lenshof, A.), pp. 256–311. Royal Society of Chemistry.Google Scholar
Sauret, A., Cébron, D., Morize, C. & Le Bars, M. 2010 Experimental and numerical study of mean zonal flows generated by librations of a rotating spherical cavity. J. Fluid Mech. 662, 260–268.Google Scholar
Sauret, A. & Le Dizès, S. 2013 Libration-induced mean flow in a spherical shell. J. Fluid Mech. 718, 181–209.Google Scholar
Schlichting, H. 1932 Berechnung ebener periodischer Grenzschichtströmungen. Phys. Z. 33 (1932), 327–335.Google Scholar
Stocchino, A., Repetto, R. & Cafferata, C. 2007 Eye rotation induced dynamics of a newtonian fluid within the vitreous cavity: the effect of the chamber shape. Phys. Med. Biol. 52 (7), 2021–2034.Google Scholar
Wang, C., Rallabandi, B. & Hilgenfeldt, S. 2013 Frequency dependence and frequency control of microbubble streaming flows. Phys. Fluids 25 (2), 022002.Google Scholar
Wiklund, M. 2012 Acoustofluidics 12: biocompatibility and cell viability in microfluidic acoustic resonators. Lab on a Chip 12 (11), 2018–2028.CrossRefGoogle ScholarPubMed
Wiklund, M., Green, R. & Ohlin, M. 2012 Acoustofluidics 14: applications of acoustic streaming in microfluidic devices. Lab on a Chip 12 (14), 2438–2451.Google Scholar
Zapryanov, Z. & Chervenivanova, E. 1981 The flow field induced by the torsional oscillations of a spherical cell containing a fluid drop. Intl J. Multiphase Flow 7 (3), 261–270.Google Scholar
Zhang, K., Chan, K. H., Liao, X. & Aurnou, J. M. 2013 The non-resonant response of fluid in a rapidly rotating sphere undergoing longitudinal libration. J. Fluid Mech. 720, 212–235.Google Scholar
Zhao, H., Sadhal, S. S. & Trinh, E. H. 1999a Internal circulation in a drop in an acoustic field. J. Acoust. Soc. Am. 106 (6), 3289–3295.Google Scholar
Zhao, H., Sadhal, S. S. & Trinh, E. H. 1999b Singular perturbation analysis of an acoustically levitated sphere: flow about the velocity node. J. Acoust. Soc. Am. 106 (2), 589–595.CrossRefGoogle Scholar