Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-29T15:35:30.880Z Has data issue: false hasContentIssue false
  • English
  • Français

Orientation of non-spherical particles in an axisymmetric random flow

Published online by Cambridge University Press:  19 February 2013

Dario Vincenzi
Dario Vincenzi*
Affiliation:
CNRS UMR 7351, Laboratoire J.-A. Dieudonné, Université de Nice Sophia Antipolis, Parc Valrose, 06108 Nice, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The dynamics of non-spherical rigid particles immersed in an axisymmetric random flow is studied analytically. The motion of the particles is described by Jeffery’s equation; the random flow is Gaussian and has short correlation time. The stationary probability density function of orientations is calculated exactly. Four regimes are identified depending on the statistical anisotropy of the flow and on the geometrical shape of the particle. 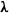If $\boldsymbol{\lambda} $ is the axis of symmetry of the flow, the four regimes are: rotation about 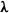$\boldsymbol{\lambda} $, tumbling motion between 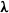$\boldsymbol{\lambda} $ and 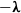$- \boldsymbol{\lambda} $, combination of rotation and tumbling, and preferential alignment with a direction oblique to 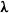$\boldsymbol{\lambda} $.

JFM classification

Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows Complex Fluids: Suspensions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 719 , 25 March 2013 , pp. 465 - 487
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Batchelor, G. K. 1946 The theory of axisymmetric turbulence. Proc. R. Soc. Lond. A 186, 480–502.Google Scholar
Bernstein, O. & Shapiro, M. 1994 Direct determination of the orientation distribution function of cylindrical particles immersed in laminar and turbulent shear flows. J. Aerosol Sci. 25, 113–136.CrossRefGoogle Scholar
Biferale, L. & Procaccia, I. 2005 Anisotropy in turbulent flows and in turbulent transport. Phys. Rep. 414, 43–164.CrossRefGoogle Scholar
Bird, R. B., Hassager, O, Armstrong, R. C. & Curtiss, C. F. 1977 Dynamics of Polymeric Liquids, vol. II. Wiley.Google Scholar
Bird, R. B., Warner, H. R. Jr & Evans, D. C. 1971 Kinetic theory and rheology of dumbbell suspensions with Brownian motion. Fortschr. Hochpolym.-Forsch. 8, 1–90.Google Scholar
Brenner, H. 1974 Rheology of a dilute suspension of axisymmetric Brownian particles. Intl J. Multiphase Flow 1, 195–341.CrossRefGoogle Scholar
Bretherton, F. P. 1962 The motion of rigid particles in a shear flow at low Reynolds number. J. Fluid Mech. 14, 284–304.CrossRefGoogle Scholar
Chandrasekhar, S. 1950 The theory of axisymmetric turbulence. Phil. Trans. R. Soc. Lond. A 242, 557–577.Google Scholar
Chang, K., Bewley, G. P. & Bodenschatz, E. 2012 Experimental study of the influence of anisotropy on the inertial scales of turbulence. J. Fluid Mech. 692, 464–481.CrossRefGoogle Scholar
Chen, J.-P. & Lamb, D. 1994 The theoretical basis for the parametrization of ice crystal habits: growth by vapour deposition. J. Atmos. Sci. 51, 1206–1221.2.0.CO;2>CrossRefGoogle Scholar
Doi, M. & Edwards, S. F. 1978 Dynamics of rod-like macromolecules in concentrated solution. 2. J. Chem. Soc. Faraday Trans. II 74, 918–932.CrossRefGoogle Scholar
Doi, M. & Edwards, S. F. 1986 The Theory of Polymer Dynamics. Oxford University Press.Google Scholar
Falkovich, G., Gawȩdzki, K. & Vergassola, M. 2001 Particles and fields in fluid turbulence. Rev. Mod. Phys. 73, 913–975.CrossRefGoogle Scholar
Gantmacher, F. R. 1959 The Theory of Matrices, vol. 1. Chelsea Publishing Company.Google Scholar
Gardiner, C. W. 1983 Handbook of Stochastic Methods. Springer.CrossRefGoogle Scholar
Gradshteyn, I. S. & Ryzhik, I. M. 1965 Table of Integrals, Series, and Products. Academic.Google Scholar
Gyr, A. & Bewersdorff, W. 1995 Drag Reduction of Turbulent Flows by Additives. Kluwer.CrossRefGoogle Scholar
Hinch, E. J. & Leal, L. G. 1972 The effect of Brownian motion on the rheological properties of a suspension of non-spherical particles. J. Fluid Mech. 52, 683–712.CrossRefGoogle Scholar
Jeffery, G. B. 1922 The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. A 102, 161–179.Google Scholar
Kloeden, P. E. & Platen, E. 1992 Numerical Solution of Stochastic Differential Equations. Springer.CrossRefGoogle Scholar
Koch, D. L. & Subramanian, G. 2011 Collective hydrodynamics of swimming microorganisms: living fluids. Annu. Rev. Fluid Mech. 43, 637–659.CrossRefGoogle Scholar
Kraichnan, R. H. 1968 Small-scale structure of a scalar field convected by turbulence. Phys. Fluids 11, 945–953.CrossRefGoogle Scholar
Krushkal, E. M. & Gallily, I. 1988 On the orientation distribution function of nonspherical aerosol particles in a general shear flow–II. The turbulent case. J. Aerosol Sci. 19, 197–211.CrossRefGoogle Scholar
Kuzuu, N. Y. & Doi, M. 1980 Nonlinear viscoelasticity of concentrated solution of rod-like polymers. Polym. J. 12, 883–890.CrossRefGoogle Scholar
Larson, R. G. 1999 The Structure and Rheology of Complex Fluids. Oxford University Press.Google Scholar
Leal, L. G. & Hinch, E. J. 1971 The effect of weak Brownian rotations on particles in shear flow. J. Fluid Mech. 46, 685–703.CrossRefGoogle Scholar
Lindborg, E. 1995 Kinematics of homogeneous axisymmetric turbulence. J. Fluid Mech. 302, 179–201.CrossRefGoogle Scholar
Minale, M. 2010 Models for the deformation of a single ellipsoidal drop: a review. Rheol. Acta 49, 789–806.CrossRefGoogle Scholar
Moakher, M. 2008 Fourth-order Cartesian tensors: old and new facts, notions and applications. Q. J. Mech. Appl. Maths 61, 181–203.CrossRefGoogle Scholar
Mortensen, P. H., Anderson, H. I., Gillissen, J. J. J. & Boersma, B. J. 2008a Dynamics of prolate ellipsoidal particles in a turbulent channel flow. Phys. Fluids 20, 093302.CrossRefGoogle Scholar
Mortensen, P. H., Anderson, H. I., Gillissen, J. J. J. & Boersma, B. J. 2008b On the orientation of ellipsoidal particles in a turbulent shear flow. Intl J. Multiphase Flow 34, 678–683.CrossRefGoogle Scholar
Newsom, R. K. & Bruce, C. W. 1998 Orientational properties of fibrous aerosols in atmospheric turbulence. J. Aerosol Sci. 29, 773–797.CrossRefGoogle Scholar
Olbricht, W. L., Rallison, J. M. & Leal, L. G. 1982 Strong flow criteria based on microstructure deformation. J. Non-Newtonian Fluid Mech. 10, 291–318.CrossRefGoogle Scholar
Olson, J. A. & Kerekes, R. J. 1998 The motion of fibres in turbulent flow. J. Fluid Mech. 377, 47–64.CrossRefGoogle Scholar
Parsa, S., Calzavarini, E., Toschi, F. & Voth, G. A. 2012 Rotation rate of rods in turbulent fluid flow. Phys. Rev. Lett. 109, 134501.CrossRefGoogle ScholarPubMed
Parsa, S., Guasto, J. S., Kishore, M., Ouellette, N. T., Gollub, J. P. & Voth, G. A. 2011 Rotation and alignment of rods in two-dimensional chaotic flow. Phys. Fluids 23, 043302.CrossRefGoogle Scholar
Parsheh, M., Brown, M. L. & Aidun, C. K. 2005 On the orientation of stiff fibres suspended in turbulent flow in a planar contraction. J. Fluid Mech. 545, 245–269.CrossRefGoogle Scholar
Petrie, J. S. P. 1999 The rheology of fibre suspensions. J. Non-Newtonian Fluid Mech. 87, 369–402.CrossRefGoogle Scholar
Puliafito, A. & Turistyn, K. 2005 Numerical study of polymer tumbling in linear shear flows. Physica D 211, 9–22.CrossRefGoogle Scholar
Pumir, A. & Wilkinson, M. 2011 Orientation statistics of small particles in turbulence. New J. Phys. 13, 093030.CrossRefGoogle Scholar
Risken, H. 1989 The Fokker–Planck Equation. Springer.Google Scholar
Robertson, H. P. 1940 The invariant theory of isotropic turbulence. Proc. Camb. Phil. Soc. 36, 209–223.CrossRefGoogle Scholar
Saintillan, D. & Shelley, M. J. 2008 Instabilities and pattern formation in active particle suspensions: kinetic theory and continuum simulations. Phys. Rev. Lett. 100, 178103.CrossRefGoogle ScholarPubMed
Shaqfeh, E. S. G. & Koch, D. L. 1992 Polymer stretch in dilute fixed beds of fibres or spheres. J. Fluid Mech. 244, 17–54.CrossRefGoogle Scholar
Shin, M. & Koch, D. L. 2005 Rotational and translational dispersion of fibres in isotropic turbulent flows. J. Fluid Mech. 540, 143–173.CrossRefGoogle Scholar
Szeri, A. J. 1993 Pattern formation in recirculating flows of suspensions of orientable particles. Phil. Trans. R. Soc. Lond. A 345, 477–506.Google Scholar
Turitsyn, K. S. 2007 Polymer dynamics in chaotic flows with a strong shear component. J. Expl Theor. Phys. 105, 655–664.CrossRefGoogle Scholar
Wilkinson, M., Bezuglyy, V. & Mehlig, B. 2009 Fingerprints of random flows. Phys. Fluids 21, 043304.CrossRefGoogle Scholar
Wilkinson, M. & Kennard, H. R. 2012 A model for alignment between microscopic rods and vorticity. J. Phys. A: Math. Theor. 45, 455502.CrossRefGoogle Scholar
Zhang, H., Ahmadi, G., Fan, F. G. & McLaughlin, J. B. 2001 Ellipsoidal particles transport and deposition in turbulent channel flows. Intl J. Multiphase Flow 27, 971–1009.CrossRefGoogle Scholar
Zimmermann, R., Gasteuil, Y., Bourgoin, M., Volk, R., Pumir, A. & Pinton, J.-F. 2011a Rotational intermittency and turbulence induced lift experienced by large particles in a turbulent flow. Phys. Rev. Lett. 106, 154501.CrossRefGoogle Scholar
Zimmermann, R., Gasteuil, Y., Bourgoin, M., Volk, R., Pumir, A. & Pinton, J.-F. 2011b Tracking the dynamics of translation and absolute orientation of a sphere in a turbulent flow. Rev. Sci. Instrum. 82, 033906.CrossRefGoogle Scholar