Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-23T18:53:04.104Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimal wing hinge position for fast ascent in a model fly

Published online by Cambridge University Press:  21 June 2018

R. M. Noest  and
Z. Jane Wang Open the ORCID record for Z. Jane Wang [Opens in a new window]
R. M. Noest
Affiliation:
Department of Physics, Cornell University, Ithaca, NY 14853, USA
Z. Jane Wang*
Affiliation:
Department of Physics, Cornell University, Ithaca, NY 14853, USA Department of Mechanical and Aerospace Engineering, Cornell University, Ithaca, NY 14853, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

It was thought that the wing hinge position can be tuned to stabilize an uncontrolled fly. However here, our Floquet stability analysis shows that the hinge position has a weak dependence on the flight stability. As long as the hinge position is within the fly’s body length, both hovering and ascending flight are unstable. Instead, there is an optimal hinge position, 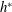$h^{\ast }$, at which the ascending speed is maximized. 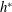$h^{\ast }$ is approximately half way between the centre of mass and the top of the body. We show that the optimal 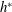$h^{\ast }$ is associated with the anti-resonance of the body–wing coupling, and is independent of the stroke amplitude. At 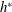$h^{\ast }$, the torque due to wing inertia nearly cancels the torque due to aerodynamic lift, minimizing the body oscillation thus maximizing the upward force. Our analysis using a simplified model of two coupled masses further predicts, 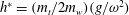$h^{\ast }=(m_{t}/2m_{w})(g/\unicode[STIX]{x1D714}^{2})$. These results suggest that the ascending speed, in addition to energetics and stability, is a trait that insects are likely to optimize.

JFM classification

Biological Fluid Dynamics: Biological Fluid Dynamics Biological Fluid Dynamics: Swimming/flying
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 849 , 25 August 2018 , pp. 498 - 509
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alben, S. 2008 Optimal flexibility of a flapping appendage in an inviscid fluid. J. Fluid Mech. 614, 355–380.Google Scholar
Alexander, R. M. 2001 Design by numbers. Nature 412 (6847), 591–591.Google Scholar
Andersen, A., Pesavento, U. & Wang, Z. J. 2005 Unsteady aerodynamics of fluttering and tumbling plates. J. Fluid Mech. 541, 65–90.Google Scholar
Berman, G. J. & Wang, Z. J. 2007 Energy-minimizing kinematics in hovering insect flight. J. Fluid Mech. 582, 153–168.Google Scholar
Bialek, W. 1987 Physical limits to sensation and perception. Annu. Rev. Biophys. Biophys. Chem. 16 (1), 455–478.Google Scholar
Chang, S. & Wang, Z. J. 2014 Predicting fruit fly’s sensing rate with insect flight simulations. Proc. Natl Acad. Sci. USA 111 (31), 11246–11251.Google Scholar
Cheng, B. & Deng, X. 2011 Translational and rotational damping of flapping flight and its dynamics and stability at hovering. IEEE Trans. Robot. 27 (5), 849–864.Google Scholar
Childress, S., Vandenberghe, N. & Zhang, J. 2006 Hovering of a passive body in an oscillating airflow. Phys. Fluids 18 (11), 117103.Google Scholar
Fraenkel, G. 1939 The function of the halteres of flies (diptera). In Proc. Zool. Soc. Lond, vol. 109, pp. 69–78. Wiley Online Library.Google Scholar
Gould, S. J. & Lewontin, R. C. 1979 The spandrels of san marco and the panglossian paradigm: a critique of the adaptationist programme. Proc. R. Soc. Lond. B 205 (1161), 581–598.Google Scholar
Grimshaw, R. 1991 Nonlinear Ordinary Differential Equations, vol. 2. CRC Press.Google Scholar
Haselsteiner, A. F., Gilbert, C. & Wang, Z. J. 2014 Tiger beetles pursue prey using a proportional control law with a delay of one half-stride. J. R. Soc. Interface 11 (95), 20140216.Google Scholar
Iams, S. & Guckenheimer, J. 2014 Flight stability of mosquitos: a reduced model. SIAM J. Appl. Maths 74 (5), 1535–1550.Google Scholar
Kuznetsov, Y. A. 2013 Elements of Applied Bifurcation Theory, vol. 112. Springer Science & Business Media.Google Scholar
Ma, K. Y., Chirarattananon, P., Fuller, S. B. & Wood, R. J. 2013 Controlled flight of a biologically inspired, insect-scale robot. Science 340 (6132), 603–607.Google Scholar
Pesavento, U. & Wang, Z. J. 2004 Falling paper: Navier–Stokes solutions, model of fluid forces, and center of mass elevation. Phys. Rev. Lett. 93 (14), 144501.Google Scholar
Pesavento, U. & Wang, Z. J. 2009 Flapping wing flight can save aerodynamic power compared to steady flight. Phys. Rev. Lett. 103 (11), 118102.Google Scholar
Ristroph, L. & Childress, S. 2014 Stable hovering of a jellyfish-like flying machine. J. R. Soc. Interface 11 (92), 20130992.Google Scholar
Ristroph, L., Ristroph, G., Morozova, S., Bergou, A. J., Chang, S., Guckenheimer, J., Wang, Z. J. & Cohen, I. 2013 Active and passive stabilization of body pitch in insect flight. J. R. Soc. Interface 10 (85), 20130237.Google Scholar
Shampine, L. F. & Gordon, M. K. 1975 Computer Solution of Ordinary Differential Equations: The Initial Value Problem, vol. 85. WH Freeman.Google Scholar
Srinivasan, M. & Ruina, A. 2006 Computer optimization of a minimal biped model discovers walking and running. Nature 439 (7072), 72–75.Google Scholar
Sun, M. 2014 Insect flight dynamics: stability and control. Rev. Mod. Phys. 86 (2), 615–646.Google Scholar
Sun, M., Wang, Z. J. & Xiong, Y. 2007 Dynamic flight stability of hovering insects. Acta Mechanica Sin. 23 (3), 231–246.Google Scholar
Tuckerman, L. B.1926 Inertia factors of ellipsoids for use in airship design. Tech. Rep., Bureau of Standards.Google Scholar
Van Breugel, F., Regan, W. & Lipson, H. 2008 From insects to machines. IEEE J. Robot. Autom. Mag. 15 (4), 68–74.Google Scholar
Wang, Z. J. 2005 Dissecting insect flight. Annu. Rev. Fluid Mech. 37, 183–210.Google Scholar
Wang, Z. J. 2016 Insect flight: from Newton’s law to neurons. Annu. Rev. Condens. Matter Phys. 7, 281–300.Google Scholar
Wang, Z. J., Birch, J. M. & Dickinson, M. H. 2004 Unsteady forces and flows in low Reynolds number hovering flight: two-dimensional computations versus robotic wing experiments. J. Expl Biol. 207 (3), 449–460.Google Scholar