Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-17T11:25:28.626Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimal transient growth in thin-interface internal solitary waves

Published online by Cambridge University Press:  12 February 2018

Pierre-Yves Passaggia Open the ORCID record for Pierre-Yves Passaggia [Opens in a new window] ,
Karl R. Helfrich  and
Brian L. White
Pierre-Yves Passaggia*
Affiliation:
Department of Marine Sciences, University of North Carolina, Chapel Hill, NC 27599, USA
Karl R. Helfrich
Affiliation:
Department of Physical Oceanography, Woods Hole Oceanographic Institution, Woods Hole, MA 02543, USA
Brian L. White
Affiliation:
Department of Marine Sciences, University of North Carolina, Chapel Hill, NC 27599, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The dynamics of perturbations to large-amplitude internal solitary waves (ISWs) in two-layered flows with thin interfaces is analysed by means of linear optimal transient growth methods. Optimal perturbations are computed through direct–adjoint iterations of the Navier–Stokes equations linearized around inviscid, steady ISWs obtained from the Dubreil-Jacotin–Long (DJL) equation. Optimal perturbations are found as a function of the ISW phase velocity $c$ (alternatively amplitude) for one representative stratification. These disturbances are found to be localized wave-like packets that originate just upstream of the ISW self-induced zone (for large enough $c$) of potentially unstable Richardson number, 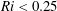$Ri<0.25$. They propagate through the base wave as coherent packets whose total energy gain increases rapidly with $c$. The optimal disturbances are also shown to be relevant to DJL solitary waves that have been modified by viscosity representative of laboratory experiments. The optimal disturbances are compared to the local Wentzel–Kramers–Brillouin (WKB) approximation for spatially growing Kelvin–Helmholtz (K–H) waves through the 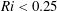$Ri<0.25$ zone. The WKB approach is able to capture properties (e.g. carrier frequency, wavenumber and energy gain) of the optimal disturbances except for an initial phase of non-normal growth due to the Orr mechanism. The non-normal growth can be a substantial portion of the total gain, especially for ISWs that are weakly unstable to K–H waves. The linear evolution of Gaussian packets of linear free waves with the same carrier frequency as the optimal disturbances is shown to result in less energy gain than found for either the optimal perturbations or the WKB approximation due to non-normal effects that cause absorption of disturbance energy into the leading face of the wave. Two-dimensional numerical calculations of the nonlinear evolution of optimal disturbance packets leads to the generation of large-amplitude K–H billows that can emerge on the leading face of the wave and that break down into turbulence in the lee of the wave. The nonlinear calculations are used to derive a slowly varying model of ISW decay due to repeated encounters with optimal or free wave packets. Field observations of unstable ISW by Moum et al. (J. Phys. Oceanogr., vol. 33 (10), 2003, pp. 2093–2112) are consistent with excitation by optimal disturbances.

JFM classification

Instability: Instability Geophysical and Geological Flows: Internal waves Waves/Free-surface Flows: Solitary waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 840 , 10 April 2018 , pp. 342 - 378
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Åkervik, E., Brandt, L., Henningson, D. S., Hœpffner, J., Marxen, O. & Schlatter, P. 2006 Steady solutions of the Navier–Stokes equations by selective frequency damping. Phys. Fluids 18 (6), 068102.Google Scholar
Alford, M. H., Peacock, T., MacKinnon, J. A., Nash, J. D., Buijsman, M. C., Centuroni, L. R., Chao, S.-Y., Chang, M.-H., Farmer, D. M., Fringer, O. B. et al. 2015 The formation and fate of internal waves in the South China Sea. Nature 521 (7550), 65–69.Google Scholar
Almgren, A., Camassa, R. & Tiron, R. 2012 Shear instability of internal solitary waves in Euler fluids with thin pycnoclines. J. Fluid Mech. 710, 324–361.Google Scholar
Almgren, A. S., Bell, J. B., Colella, P., Howell, L. H. & Welcome, M. L. 1998 A conservative adaptive projection method for the variable density incompressible Navier–Stokes equations. J. Comput. Phys. 142, 1–46.Google Scholar
Barad, M. F. & Fringer, O. B. 2010 Simulations of shear instabilities in interfacial gravity waves. J. Fluid Mech. 644, 61–95.CrossRefGoogle Scholar
Brandt, L., Sipp, D., Pralits, J. O. & Marquet, O. 2011 Effect of base-flow variation in noise amplifiers: the flat-plate boundary layer. J. Fluid Mech. 687, 503–528.Google Scholar
Camassa, R. & Viotti, C. 2012 On the response of large-amplitude internal waves to upstream disturbances. J. Fluid Mech. 702, 59–88.Google Scholar
Carr, M., Franklin, J., King, S. E., Davies, P. A., Grue, J. & Dritschel, D. G. 2017 The characteristics of billows generated by internal solitary waves. J. Fluid Mech. 812, 541–577.CrossRefGoogle Scholar
Carr, M., Fructus, D., Grue, J., Jensen, A. & Davies, P. A. 2008 Convectively induced shear instability in large amplitude internal solitary waves. Phys. Fluids 20 (12), 126601.Google Scholar
Carr, M., King, S. E. & Dritschel, D. G. 2011 Numerical simulation of shear-induced instabilities in internal solitary waves. J. Fluid Mech. 683, 263–288.Google Scholar
Carr, M., King, S. E. & Dritschel, D. G. 2012 Instability in internal solitary waves with trapped cores. Phys. Fluids 24 (1), 016601.Google Scholar
Chomaz, J.-M. 2005 Global instabilities in spatially developing flows: non-normality and nonlinearity. Annu. Rev. Fluid Mech. 37 (1), 357–392.Google Scholar
Cunha, G., Passaggia, P.-Y. & Lazareff, M. 2015 Optimization of the selective frequency damping parameters using model reduction. Phys. Fluids 27 (9), 094103.Google Scholar
Davis, R. E. & Acrivos, A. 1967 Solitary internal waves in deep water. J. Fluid Mech. 29, 593–607.Google Scholar
Dubriel-Jacotin, M. L. 1934 Sur la determination rigoureuse des ondes permanentes periodiques d’amplitude finie. J. Math. Pure Appl. 13, 217–291.Google Scholar
Farrell, B. F. & Ioannou, P. J. 1993a Optimal excitation of three-dimensional perturbations in viscous constant shear flow. Phys. Fluids 5 (6), 1390–1400.CrossRefGoogle Scholar
Farrell, B. F. & Ioannou, P. J. 1993b Transient development of perturbations in stratified shear flow. J. Atmos. Sci. 50 (14), 2201–2214.Google Scholar
Fructus, D., Carr, M., Grue, J., Jensen, A. & Davies, P. A. 2009 Shear-induced breaking of large internal solitary waves. J. Fluid Mech. 620, 1–29.Google Scholar
Grimshaw, R., Pelinovsky, E. & Talipova, T. 2003 Damping of large-amplitude solitary waves. Wave Motion 37, 351–364.Google Scholar
Grimshaw, R., Pelinovsky, E., Talipova, T. & Kurkina, A. 2010 Internal solitary waves: propagation, deformation and disintegration. Nonlinear Process. Geophys. 17, 633–649.Google Scholar
Grue, J. 2015 Nonlinear interfacial wave formation in three dimensions. J. Fluid Mech. 767, 735–762.Google Scholar
Grue, J., Jensen, A., Rusås, P.-O. & Sveen, J. K. 2000 Breaking and broadening of internal solitary waves. J. Fluid Mech. 413, 181–217.Google Scholar
Helfrich, K. R. & Melville, W. K. 2006 Long nonlinear internal waves. Annu. Rev. Fluid Mech. 38, 395–425.Google Scholar
Helfrich, K. R. & White, B. L. 2010 A model for large-amplitude internal solitary waves with trapped cores. Nonlinear Process. Geophys. 17, 303–318.Google Scholar
Huang, X., Chen, Z., Zhao, W., Zhang, Z., Zhou, C., Yang, Q. & Tian, J. 2016 An extreme internal solitary wave event observed in the northern South China Sea. Sci. Rep. 6, 30041.Google Scholar
Jackson, C. R., Da Silva, J. C. B. & Jeans, G. 2012 The generation of nonlinear internal waves. Oceanogr. 22 (2), 109–123.Google Scholar
Joslin, R. D., Gunzburger, M. D., Nicolaides, R. A., Erlebacher, G. & Hussaini, M. Y. 1997 Self-contained automated methodology for optimal flow control. AIAA J. 35 (5), 816–824.Google Scholar
Kaminski, A. K., Caulfield, C. P. & Taylor, J. R. 2014 Transient growth in strongly stratified shear layers. J. Fluid Mech. 758, R4 (12 pages).Google Scholar
Lamb, K. G. 2003 Shoaling solitary internal waves: on a criterion for the formation of waves with trapped cores. J. Fluid Mech. 478, 81–100.Google Scholar
Lamb, K. G. 2008 On the calculation of the available potential energy of an isolated perturbation in a density-stratified fluid. J. Fluid Mech. 597, 415–427.Google Scholar
Lamb, K. G. & Farmer, D. 2011 Instabilities in an internal solitary-like wave on the oregon shelf. J. Phys. Oceanogr. 41 (1), 67–87.Google Scholar
Lamb, K. G. & Wan, B. 1998 Conjugate flows and flat solitary waves for a continuously stratified fluid. Phys. Fluids 10, 2061–2079.Google Scholar
Lele, S. K. 1992 Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 103, 16–42.Google Scholar
Lien, R.-C., D’Asaro, E. A., Henyey, F., Chang, M. H., Tang, T.-Y. & Yang, Y.-J. 2012 Trapped core formation within a shoaling nonlinear internal wave. J. Phys. Oceanogr. 42, 511–525.CrossRefGoogle Scholar
Lien, R.-C., Henyey, F., Ma, B. & Yang, Y. J. 2014 Large-amplitude internal solitary waves observed in the northern South China Sea: properties and energetics. J. Phys. Oceanogr. 44 (4), 1095–1115.Google Scholar
Long, R. R. 1953 Some aspects of the flow of stratified fluid. I. A theoretical investigation. Tellus 5, 42–57.CrossRefGoogle Scholar
Luchini, P. & Bottaro, A. 2014 Adjoint equations in stability analysis. Annu. Rev. Fluid Mech. 46, 493–517.Google Scholar
Luzzatto-Fegiz, P. & Helfrich, K. R. 2014 Laboratory experiments and simulations for solitary internal waves with trapped cores. J. Fluid Mech. 757, 354–380.Google Scholar
Marquillie, M. & Ehrenstein, U. 2002 Numerical simulation of a separating boundary-layer flow. Comput. Fluids 31, 683–693.Google Scholar
Marquillie, M. & Ehrenstein, U. 2003 On the onset of nonlinear oscillations in a separating boundary-layer flow. J. Fluid Mech. 490, 169–188.Google Scholar
Matlab2014 An adaptive boundary value solver for ordinary differential equations. https://www.mathworks.com/help/matlab/ref/bvp5c.html, accessed 17 June 2017.Google Scholar
Moum, J. N., Farmer, D. M., Smyth, W. D., Armi, L. & Vagle, S. 2003 Structure and generation of turbulence at interfaces strained by internal solitary waves propagating shoreward over the continental shelf. J. Phys. Oceanogr. 33 (10), 2093–2112.2.0.CO;2>CrossRefGoogle Scholar
Moum, J. N., Farmer, D. M., Smyth, W. D., Armi, L. & Vagle, S. 2007 Dissipative losses in non-linear internal waves propagating across the continental shelf. J. Phys. Oceanogr. 37, 1989–1995.Google Scholar
Oppenheim, A. V., Schafer, R. W. & Buck, J. R. 1999 Discrete-Time Signal Processing. Prentice Hall.Google Scholar
Orr, W. M. F. 1907 The stability or instability of the steady motions of a perfect liquid and of a viscous liquid. Part I: a perfect liquid. Proc. R. Irish Acad. A 27, 9–68.Google Scholar
Passaggia, P.-Y. & Ehrenstein, U. 2013 Adjoint based optimization and control of a separated boundary-layer flow. Eur. J. Mech. (B/Fluids) 41, 169–177.CrossRefGoogle Scholar
Sandstrom, H. & Elliott, J. A. 1984 Internal tide and solitons on the Scotian Shelf: a nutrient pump at work. J. Geophys. Res. 89 (C4), 6415–6426.Google Scholar
Schmid, P. J. 2007 Nonmodal stability theory. Annu. Rev. Fluid Mech. 39, 129–162.Google Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows, Applied Mathematical Sciences. Springer.Google Scholar
Scotti, A., Beardsley, R. & Butman, B. 2006 On the interpretation of energy and energy fluxes of nonlinear internal waves: an example from Massachusetts Bay. J. Fluid Mech. 561, 103–112.Google Scholar
Shroyer, E. L., Moum, J. N. & Nash, J. D. 2010a Energy transformations and dissipation of nonlinear internal waves over New Jersey’s continental shelf. Nonlinear Process. Geophys. 17 (4), 345–360.Google Scholar
Shroyer, E. L., Moum, J. N. & Nash, J. D. 2010b Mode 2 waves on the continental shelf: Ephemeral components of the nonlinear internal wavefield. J. Geophys. Res. 115 (C7).Google Scholar
Sipp, D. & Marquet, O. 2013 Characterization of noise amplifiers with global singular modes: the case of the leading-edge flat-plate boundary layer. Theor. Comput. Fluid Dyn. 27 (5), 617.CrossRefGoogle Scholar
Squire, H. B. 1933 On the stability for three-dimensional disturbances of viscous fluid flow between parallel walls. Proc. R. Soc. Lond. A 142, 621–628.Google Scholar
St. Laurent, L. C., Simmons, H. L., Tang, T. Y. & Wang, Y. H. 2011 Turbulent properties of internal waves in the South China Sea. Oceanogr. 24, 78–87.Google Scholar
Stanton, T. P. & Ostrovsky, L. A. 1998 Observations of highly nonlinear internal solitons over the Continental Shelf. Geophys. Res. Lett. 25, 2695–2698.CrossRefGoogle Scholar
Staquet, C. & Sommeria, J. 2002 Internal gravity waves: from instabilities to turbulence. Annu. Rev. Fluid Mech. 34 (1), 559–593.Google Scholar
Stastna, M. & Lamb, K. 2002 Large fully nonlinear internal solitary waves: the effect of background current. Phys. Fluids 14, 2987–2999.Google Scholar
Troy, C. D. & Koseff, J. R. 2005 The instability and breaking of long internal waves. J. Fluid Mech. 543, 107–136.CrossRefGoogle Scholar
Zhang, S. & Alford, M. H. 2015 Instabilities in nonlinear internal waves on the Washington continental shelf. J. Geophys. Res. 120 (7), 5272–5283.Google Scholar