Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Alizard, Frédéric
2015.
Linear stability of optimal streaks in the log-layer of turbulent channel flows.
Physics of Fluids,
Vol. 27,
Issue. 10,
Rinaldi, Enrico
Patel, Ashish
Schlatter, Philipp
and
Pecnik, Rene
2017.
Linear stability of buffer layer streaks in turbulent channels with variable density and viscosity.
Physical Review Fluids,
Vol. 2,
Issue. 11,
Nichols, Joseph W.
Larsson, Johan
Bernardini, Matteo
and
Pirozzoli, Sergio
2017.
Stability and modal analysis of shock/boundary layer interactions.
Theoretical and Computational Fluid Dynamics,
Vol. 31,
Issue. 1,
p.
33.
Uzun, Ali
Davis, Timothy B.
Alvi, Farrukh S.
and
Hussaini, M. Yousuff
2017.
Optimally growing boundary layer disturbances in a convergent nozzle preceded by a circular pipe.
Theoretical and Computational Fluid Dynamics,
Vol. 31,
Issue. 3,
p.
317.
Cossu, Carlo
and
Hwang, Yongyun
2017.
Self-sustaining processes at all scales in wall-bounded turbulent shear flows.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 375,
Issue. 2089,
p.
20160088.
Dawson, Scott T.M.
and
McKeon, Beverley J.
2020.
Prediction of resolvent mode shapes in supersonic turbulent boundary layers.
International Journal of Heat and Fluid Flow,
Vol. 85,
Issue. ,
p.
108677.
Tang, Jiupeng
Zhao, Zhiye
Wan, Zhen-Hua
and
Liu, Nan-Sheng
2020.
On the near-wall structures and statistics of fluctuating pressure in compressible turbulent channel flows.
Physics of Fluids,
Vol. 32,
Issue. 11,
Wang, Xu
Wang, Zhenguo
Sun, Mingbo
Wang, Qiancheng
and
Hu, Zhiwei
2020.
Effects of favorable pressure gradient on turbulence structures and statistics of a flat-plate supersonic turbulent boundary layer.
Physics of Fluids,
Vol. 32,
Issue. 2,
Xu, Dehao
Wang, Jianchun
Wan, Minping
Yu, Changping
Li, Xinliang
and
Chen, Shiyi
2021.
Effect of wall temperature on the kinetic energy transfer in a hypersonic turbulent boundary layer.
Journal of Fluid Mechanics,
Vol. 929,
Issue. ,
Xu, Dehao
Wang, Jianchun
Wan, Minping
Yu, Changping
Li, Xinliang
and
Chen, Shiyi
2021.
Compressibility effect in hypersonic boundary layer with isothermal wall condition.
Physical Review Fluids,
Vol. 6,
Issue. 5,
Gorbushin, Anton
Osipova, Svetlana
and
Zametaev, Vladimir
2021.
Mean Parameters of an Incompressible Turbulent Boundary Layer on the Wind Tunnel Wall at Very High Reynolds Numbers.
Flow, Turbulence and Combustion,
Vol. 107,
Issue. 1,
p.
31.
Guzmán-Iñigo, Juan
Yang, Dong
Gaudron, Renaud
and
Morgans, Aimee S.
2022.
On the scattering of entropy waves at sudden area expansions.
Journal of Sound and Vibration,
Vol. 540,
Issue. ,
p.
117261.
Alizard, Frédéric
Gibis, Tobias
Selent, Björn
Rist, Ulrich
and
Wenzel, Christoph
2022.
Stochastic receptivity of laminar compressible boundary layers: An input-output analysis.
Physical Review Fluids,
Vol. 7,
Issue. 7,
Chen, Xianliang
Cheng, Cheng
Fu, Lin
and
Gan, Jianping
2023.
Linear response analysis of supersonic turbulent channel flows with a large parameter space.
Journal of Fluid Mechanics,
Vol. 962,
Issue. ,
Chen, Xianliang
Cheng, Cheng
Gan, Jianping
and
Fu, Lin
2023.
Study of the linear models in estimating coherent velocity and temperature structures for compressible turbulent channel flows.
Journal of Fluid Mechanics,
Vol. 973,
Issue. ,
Xu, Dehao
Wang, Jianchun
and
Chen, Shiyi
2023.
Reynolds number and wall cooling effects on correlations between the thermodynamic variables in hypersonic turbulent boundary layers.
Journal of Fluid Mechanics,
Vol. 965,
Issue. ,
Gaudron, Renaud
Guzmán Iñigo, Juan
and
Morgans, Aimee S.
2023.
Variation of Acoustic Energy Across Sudden Area Expansions Sustaining a Subsonic Flow.
AIAA Journal,
Vol. 61,
Issue. 1,
p.
378.
Cheng, Cheng
Chen, Xianliang
Zhu, Wenkai
Shyy, Wei
and
Fu, Lin
2024.
Progress in physical modeling of compressible wall-bounded turbulent flows.
Acta Mechanica Sinica,
Vol. 40,
Issue. 1,
Yu, Ming
Dong, SiWei
Guo, QiLong
Tang, ZhiGong
Yuan, XianXu
and
Xu, ChunXiao
2024.
Characterization of very-large-scale motions in supersonic and hypersonic turbulent boundary layers.
Journal of Fluid Mechanics,
Vol. 980,
Issue. ,
Yu, Ming
Dong, SiWei
Yuan, XianXu
and
Xu, ChunXiao
2024.
Statistics and dynamics of coherent structures in compressible wall-bounded turbulence.
Science China Physics, Mechanics & Astronomy,
Vol. 67,
Issue. 12,
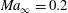 $\mathit{Ma}_{\infty }=0.2$, 2, 3 and 4. Weak effects of compressibility on the characteristics length and the orientation angles are observed for both the inner- and the outer-layer modes. Furthermore, taking into account the effects of mean density variations, a universal behaviour is suggested for the optimal modes that populate the log layer, regardless of the Mach number. The relevance of the optimal modes in describing the near-wall layer dynamics and the eddies that populate the outer region is discussed.
$\mathit{Ma}_{\infty }=0.2$, 2, 3 and 4. Weak effects of compressibility on the characteristics length and the orientation angles are observed for both the inner- and the outer-layer modes. Furthermore, taking into account the effects of mean density variations, a universal behaviour is suggested for the optimal modes that populate the log layer, regardless of the Mach number. The relevance of the optimal modes in describing the near-wall layer dynamics and the eddies that populate the outer region is discussed.