Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-29T15:35:07.847Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimal Taylor–Couette flow: direct numerical simulations

Published online by Cambridge University Press:  19 February 2013

Rodolfo Ostilla ,
Richard J. A. M. Stevens ,
Siegfried Grossmann ,
Roberto Verzicco  and
Detlef Lohse
Rodolfo Ostilla*
Affiliation:
Department of Science and Technology, Mesa+ Institute and J. M. Burgers Centre for Fluid Dynamics, University of Twente, P.O. Box 217, 7500 AE Enschede, The Netherlands
Richard J. A. M. Stevens
Affiliation:
Department of Science and Technology, Mesa+ Institute and J. M. Burgers Centre for Fluid Dynamics, University of Twente, P.O. Box 217, 7500 AE Enschede, The Netherlands Department of Mechanical Engineering, Johns Hopkins University, 3400 N. Charles Street, Baltimore, MD 21218, USA
Siegfried Grossmann
Affiliation:
Department of Physics, University of Marburg, Renthof 6, D-35032 Marburg, Germany
Roberto Verzicco
Affiliation:
Department of Science and Technology, Mesa+ Institute and J. M. Burgers Centre for Fluid Dynamics, University of Twente, P.O. Box 217, 7500 AE Enschede, The Netherlands Dipartimento di Ingegneria Meccanica, University of Rome ‘Tor Vergata’, Via del Politecnico 1, Roma 00133, Italy
Detlef Lohse
Affiliation:
Department of Science and Technology, Mesa+ Institute and J. M. Burgers Centre for Fluid Dynamics, University of Twente, P.O. Box 217, 7500 AE Enschede, The Netherlands
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

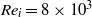We numerically simulate turbulent Taylor–Couette flow for independently rotating inner and outer cylinders, focusing on the analogy with turbulent Rayleigh–Bénard flow. Reynolds numbers of $R{e}_{i} = 8\times 1{0}^{3} $ and 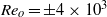$R{e}_{o} = \pm 4\times 1{0}^{3} $ of the inner and outer cylinders, respectively, are reached, corresponding to Taylor numbers 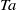$Ta$ up to 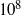$1{0}^{8} $. Effective scaling laws for the torque and other system responses are found. Recent experiments with the Twente Turbulent Taylor–Couette (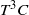${T}^{3} C$) setup and with a similar facility in Maryland at very high Reynolds numbers have revealed an optimum transport at a certain non-zero rotation rate ratio 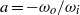$a= - {\omega }_{o} / {\omega }_{i} $ of about ${a}_{\mathit{opt}} = 0. 33$. For large enough 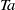$Ta$ in the numerically accessible range we also find such an optimum transport at non-zero counter-rotation. The position of this maximum is found to shift with the driving, reaching a maximum of 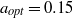${a}_{\mathit{opt}} = 0. 15$ for 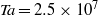$Ta= 2. 5\times 1{0}^{7} $. An explanation for this shift is elucidated, consistent with the experimental result that 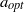${a}_{\mathit{opt}} $ becomes approximately independent of the driving strength for large enough Reynolds numbers. We furthermore numerically calculate the angular velocity profiles and visualize the different flow structures for the various regimes. By writing the equations in a frame co-rotating with the outer cylinder a link is found between the local angular velocity profiles and the global transport quantities.

JFM classification

Convection: Convection
Type
Papers
Information
Journal of Fluid Mechanics , Volume 719 , 25 March 2013 , pp. 14 - 46
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G. 1974 Low temperature studies of the Rayleigh–Bénard instability and turbulence. Phys. Rev. Lett. 33, 1185–1188.Google Scholar
Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large-scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.Google Scholar
Andereck, C. D., Liu, S. S. & Swinney, H. L. 1986 Flow regimes in a circular Couette system with independently rotating cylinders. J. Fluid Mech. 164, 155.Google Scholar
Behringer, R. P. 1985 Rayleigh–Bénard convection and turbulence in liquid-helium. Rev. Mod. Phys. 57, 657–687.Google Scholar
Bilson, M. & Bremhorst, K. 2007 Direct numerical simulation of turbulent Taylor–Couette flow. J. Fluid Mech. 579, 227.Google Scholar
Bodenschatz, E., Pesch, W. & Ahlers, G. 2000 Recent developments in Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 32, 709–778.Google Scholar
Brauckmann, H. & Eckhardt, B. 2013 Direct numerical simulations of local and global torque in Taylor–Couette flow up to $Re= 30. 000$ . J. Fluid Mech. 718, 398–427.Google Scholar
Busse, F. H. 1967 The stability of finite amplitude cellular convection and its relation to an extremum principle. J. Fluid Mech. 30, 625–649.Google Scholar
Chandrasekhar, S. 1981 Hydrodynamic and Hydromagnetic Stability. Dover.Google Scholar
Coughlin, K. & Marcus, P. S. 1996 Turbulent bursts in Couette–Taylor flow. Phys. Rev. Lett. 77 (11), 2214–2217.CrossRefGoogle ScholarPubMed
Cross, M. C. & Hohenberg, P. C. 1993 Pattern formation outside of equilibrium. Rev. Mod. Phys. 65 (3), 851.Google Scholar
Dong, S. 2007 Direct numerical simulation of turbulent Taylor–Couette flow. J. Fluid Mech. 587, 373–393.CrossRefGoogle Scholar
Dong, S. 2008 Turbulent flow between counter-rotating concentric cylinders: a direct numerical simulation study. J. Fluid Mech. 615, 371–399.CrossRefGoogle Scholar
Drazin, P. G. & Reid, W. H. 1981 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Eckhardt, B., Grossmann, S. & Lohse, D. 2007 Torque scaling in turbulent Taylor–Couette flow between independently rotating cylinders. J. Fluid Mech. 581, 221–250.Google Scholar
Esser, A. & Grossmann, S. 1996 Analytic expression for Taylor–Couette stability boundary. Phys. Fluids 8, 1814–1819.Google Scholar
Fasel, H. & Booz, O. 1984 Numerical investigation of supercritical Taylor-vortex flow for a wide gap. J. Fluid Mech. 138, 21–52.Google Scholar
Gebhardt, Th. & Grossmann, S. 1993 The Taylor–Couette eigenvalue problem with independently rotating cylinders. Z. Phys. B 90 (4), 475–490.Google Scholar
van Gils, D. P. M., Bruggert, G. W., Lathrop, D. P., Sun, C. & Lohse, D. 2011a The Twente Turbulent Taylor–Couette ( ${T}^{3} C$ ) facility: strongly turbulent (multi-phase) flow between independently rotating cylinders. Rev. Sci. Instrum. 82, 025105.CrossRefGoogle Scholar
van Gils, D. P. M., Huisman, S. G., Bruggert, G. W., Sun, C. & Lohse, D. 2011b Torque scaling in turbulent Taylor–Couette flow with co- and counter-rotating cylinders. Phys. Rev. Lett. 106, 024502.Google Scholar
van Gils, D. P. M., Huisman, S. G., Grossmann, S., Sun, C. & Lohse, D. 2012 Optimal Taylor–Couette turbulence. J. Fluid Mech. 706, 118.Google Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying view. J. Fluid. Mech. 407, 27–56.Google Scholar
Grossmann, S. & Lohse, D. 2001 Thermal convection for large Prandtl numbers. Phys. Rev. Lett. 86, 3316–3319.Google Scholar
Grossmann, S. & Lohse, D. 2011 Multiple scaling in the ultimate regime of thermal convection. Phys. Fluids 23, 045108.CrossRefGoogle Scholar
Haim, D. & Pismen, L. M. 1994 Performance of a photochemical reactor in the regime of Taylor–Görtler vortical flow. Chem. Engng Sci. 49 (8), 1119–1129.CrossRefGoogle Scholar
He, X., Funfschilling, D., Nobach, H., Bodenschatz, E. & Ahlers, G. 2011 Transition to the ultimate state of turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 108, 024502.Google Scholar
Huisman, S. G., van Gils, D. P. M., Grossmann, S., Sun, C. & Lohse, D. 2012 Ultimate turbulent Taylor–Couette flow. Phys. Rev. Lett. 108, 024501.CrossRefGoogle ScholarPubMed
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.Google Scholar
Kadanoff, L. P. 2001 Turbulent heat flow: structures and scaling. Phys. Today 54 (8), 34–39.Google Scholar
Lathrop, D. P., Fineberg, J. & Swinney, H. S. 1992a Transition to shear-driven turbulence in Couette–Taylor flow. Phys. Rev. A 46, 6390–6405.Google Scholar
Lathrop, D. P., Fineberg, J. & Swinney, H. S. 1992b Turbulent flow between concentric rotating cylinders at large Reynolds numbers. Phys. Rev. Lett. 68, 1515–1518.CrossRefGoogle Scholar
Lewis, G. S. & Swinney, H. L. 1999 Velocity structure functions, scaling, and transitions in high-Reynolds-number Couette–Taylor flow. Phys. Rev. E 59, 5457–5467.Google Scholar
Lohse, D. & Xia, K.-Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.Google Scholar
Lorenz, E. N. 1963 Deterministic nonperiodic flow. J. Atmos. Sci. 20, 130–141.Google Scholar
Paoletti, M. S. & Lathrop, D. P. 2011 Angular momentum transport in turbulent flow between independently rotating cylinders. Phys. Rev. Lett. 106, 024501.CrossRefGoogle ScholarPubMed
Pfister, G. & Rehberg, I. 1981 Space dependent order parameter in circular Couette flow transitions. Phys. Lett. 83, 19–22.Google Scholar
Pfister, G., Schmidt, H., Cliffe, K. A. & Mullin, T. 1988 Bifurcation phenomena in Taylor–Couette flow in a very short annulus. J. Fluid Mech. 191, 1–18.Google Scholar
Pirro, D. & Quadrio, M. 2008 Direct numerical simulation of turbulent Taylor–Couette flow. Eur. J. Mech. (B/Fluids) 27, 552.Google Scholar
Ravelet, F., Delfos, R. & Westerweel, J. 2010 Influence of global rotation and Reynolds number on the large-scale features of a turbulent Taylor–Couette flow. Phys. Fluids 22 (5), 055103.CrossRefGoogle Scholar
Siggia, E. D. 1994 High Rayleigh number convection. Annu. Rev. Fluid Mech. 26, 137–168.Google Scholar
Smith, G. P. & Townsend, A. A. 1982 Turbulent Couette flow between concentric cylinders at large Taylor numbers. J. Fluid Mech. 123, 187–217.Google Scholar
Stevens, R. J. A. M., Verzicco, R. & Lohse, D. 2010 Radial boundary layer structure and Nusselt number in Rayleigh–Bénard convection. J. Fluid Mech. 643, 495–507.Google Scholar
Strogatz, S. H. 1994 Nonlinear Dynamics and Chaos. Perseus.Google Scholar
Sugiyama, K., Calzavarini, E., Grossmann, S. & Lohse, D. 2007 Non-Oberbeck–Boussinesq effects in Rayleigh–Bénard convection: beyond boundary-layer theory. Europhys. Lett. 80, 34002.Google Scholar
Taylor, G. I. 1936 Fluid friction between rotating cylinders. Proc. R. Soc. Lond. A 157, 546–564.Google Scholar
Tong, P., Goldburg, W. I., Huang, J. S. & Witten, T. A. 1990 Anisotropy in turbulent drag reduction. Phys. Rev. Lett. 65, 2780–2783.Google Scholar
Verzicco, R. & Orlandi, P. 1996 A finite-difference scheme for three-dimensional incompressible flow in cylindrical coordinates. J. Comput. Phys. 123, 402–413.Google Scholar
Wendt, F. 1933 Turbulente Strömungen zwischen zwei rotierenden Zylindern. Ing.-Arch. 4, 577–595.Google Scholar