Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-26T12:57:59.988Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimal mixing in two-dimensional stratified plane Poiseuille flow at finite Péclet and Richardson numbers

Published online by Cambridge University Press:  23 August 2018

F. Marcotte Open the ORCID record for F. Marcotte [Opens in a new window]  and
C. P. Caulfield Open the ORCID record for C. P. Caulfield [Opens in a new window]
F. Marcotte
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
C. P. Caulfield*
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK BP Institute, University of Cambridge, Madingley Road, Cambridge CB3 0EZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the nonlinear optimisation of irreversible mixing induced by an initial finite amplitude perturbation of a statically stable density-stratified fluid with kinematic viscosity $\unicode[STIX]{x1D708}$ and density diffusivity $\unicode[STIX]{x1D705}$. The initial diffusive error function density distribution varies continuously so that 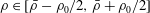$\unicode[STIX]{x1D70C}\in [\bar{\unicode[STIX]{x1D70C}}-\unicode[STIX]{x1D70C}_{0}/2,\bar{\unicode[STIX]{x1D70C}}+\unicode[STIX]{x1D70C}_{0}/2]$. A constant pressure gradient is imposed in a plane two-dimensional channel of depth 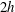$2h$. We consider flows with a finite Péclet number 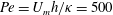$Pe=U_{m}h/\unicode[STIX]{x1D705}=500$ and Prandtl number 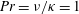$Pr=\unicode[STIX]{x1D708}/\unicode[STIX]{x1D705}=1$, and a range of bulk Richardson numbers 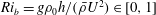$Ri_{b}=g\unicode[STIX]{x1D70C}_{0}h/(\bar{\unicode[STIX]{x1D70C}}U^{2})\in [0,1]$ where 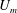$U_{m}$ is the maximum flow speed of the laminar parallel flow, and 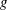$g$ is the gravitational acceleration. We use the constrained variational direct-adjoint-looping (DAL) method to solve two optimisation problems, extending the optimal mixing results of Foures et al. (J. Fluid Mech., vol. 748, 2014, pp. 241–277) to stratified flows, where the irreversible mixing of the active scalar density leads to a conversion of kinetic energy into potential energy. We identify initial perturbations of fixed finite kinetic energy which maximise the time-averaged perturbation kinetic energy developed over a finite time interval, and initial perturbations that minimise the value (at a target time, chosen to be 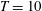$T=10$) of a ‘mix-norm’ as first introduced by Mathew et al. (Physica D, vol. 211, 2005, pp. 23–46), further discussed by Thiffeault (Nonlinearity, vol. 25, 2012, pp. 1–44) and shown by Foures et al. (2014) to be a computationally efficient and robust proxy for identifying perturbations that minimise the long-time variance of a scalar distribution. We demonstrate, for all bulk Richardson numbers considered, that the time-averaged kinetic-energy maximising perturbations are significantly suboptimal at mixing compared to the mix-norm minimising perturbations, and also that minimising the mix-norm remains (for density-stratified flows) a good proxy for identifying perturbations which minimise the variance at long times. Although increasing stratification reduces the mixing in general, mix-norm minimising optimal perturbations can still trigger substantial mixing for 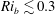$Ri_{b}\lesssim 0.3$. By considering the time evolution of the kinetic energy and potential energy reservoirs, we find that such perturbations lead to a flow which, through Taylor dispersion, very effectively converts perturbation kinetic energy into ‘available potential energy’, which in turn leads rapidly and irreversibly to thorough and efficient mixing, with little energy returned to the kinetic-energy reservoirs.

JFM classification

Flow Control: Mixing enhancement Geophysical and Geological Flows: Stratified flows Mathematical Foundations: Variational methods
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 853 , 25 October 2018 , pp. 359 - 385
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aamo, O. M., Krstic, M. & Bewley, T. R. 2003 Control of mixing by boundary feedback in 2D channel flow. Automatica 39, 1597–1606.Google Scholar
Balogh, A., Aamo, O. M. & Krstic, M. 2005 Optimal mixing enhancement in 3D pipe flow. IEEE Trans. Control Syst. Technol. 13, 27–41.Google Scholar
Caulfield, C. P. & Peltier, W. R. 2000 The anatomy of the mixing transition in homogeneous and stratified free shear layers. J. Fluid Mech. 413, 1–47.Google Scholar
Chorin, A. J. 1967 The numerical solution of the Navier–Stokes equations for an incompressible fluid. Bull. Am. Math. Soc. 73, 928–931.Google Scholar
Chorin, A. J. 1968 Numerical solution of the Navier–Stokes equations. Maths Comput. 22, 745–762.Google Scholar
Doering, C. R. & Thiffeault, J.-L. 2006 Multiscale mixing efficiencies for steady sources. Phys. Rev. E 74 (2), 025301(R).Google Scholar
Foures, D. P. G., Caulfield, C. P. & Schmid, P. J. 2013 Localization of flow structures using ∞-norm optimisation. J. Fluid Mech. 729, 672–701.Google Scholar
Foures, D. P. G., Caulfield, C. P. & Schmid, P. J. 2014 Optimal mixing in two-dimensional plane Poiseuille flow at finite Péclet number. J. Fluid Mech. 748, 241–277.Google Scholar
Hill, D. 1995 Adjoint systems and their role in the receptivity problem for boundary layers. J. Fluid Mech. 292, 181–204.Google Scholar
Kerswell, R. R., Pringle, C. C. T. & Willis, A. P. 2014 An optimisation approach for analysing nonlinear stability with transition to turbulence in fluids as an exemplar. Rep. Prog. Phys. 77, 085901.Google Scholar
Kukukova, A., Aubin, J. & Kresta, S. M. 2009 A new definition of mixing and segregation: three dimensions of a key process variable. Chem. Engng Res. Des. 87, 633–647.Google Scholar
Lin, Z., Thiffeault, J. L. & Doering, C. R. 2011 Optimal stirring strategies for passive scalar mixing. J. Fluid Mech. 675, 465–476.Google Scholar
Luchini, P. & Bottaro, A. 2014 Adjoint equations in stability analysis. Annu. Rev. Fluid Mech. 46, 493–517.Google Scholar
Lorenz, E. N. 1955 Available potential energy and the maintenance of the general circulation. Tellus 7 (2), 141–276.Google Scholar
Mashayek, A., Caulfield, C. P. & Peltier, W. R. 2013 Time-dependent, non-monotonic mixing in stratified turbulent shear flows: implications for oceanographic estimates of buoyancy flux. J. Fluid Mech. 736, 570–593.Google Scholar
Mashayek, A., Caulfield, C. P. & Peltier, W. R. 2017 Role of overturns in optimal mixing in stratified mixing layers. J. Fluid Mech. 826, 522–552.Google Scholar
Mathew, G., Mezic, I. & Petzold, L. 2005 A multiscale measure for mixing. Physica D 211, 23–46.Google Scholar
Mathew, G., Mezic, I., Grivopoulos, S., Vaidya, U. & Petzold, L. 2007 Optimal control of mixing in Stokes fluid flows. J. Fluid Mech. 580, 261–281.Google Scholar
Orr, W. M. F. 1907 The stability or instability of the steady motions of a perfect liquid and of a viscous liquid. Part I: a perfect liquid, part II: a viscous liquid. Proc. R. Irish Acad. A 27, 9–138.Google Scholar
Osborn, T. R. 1980 Estimates of the local rate of vertical diffusion from dissipation measurements. J. Phys. Oceanogr. 10, 83–89.Google Scholar
Peltier, W. R. & Caulfield, C. P. 2003 Mixing efficiency in stratified shear flows. Annu. Rev. Fluid Mech. 35, 135–167.Google Scholar
Phillips, O. M. 1972 Turbulence in a strongly stratified fluid – is it unstable? Deep Sea Res. 19, 79–81.Google Scholar
Schmid, P. 2007 Nonmodal stability theory. Annu. Rev. Fluid Mech. 39, 129–162.Google Scholar
Tailleux, R. 2013 Available potential energy and exergy in stratified fluids. Annu. Rev. Fluid Mech. 45, 35–58.Google Scholar
Taylor, G. I. 1953 Dispersion of soluble matter in solvent flowing slowly through a tube. Proc. R. Soc. Lond. A 219, 186–203.Google Scholar
Thiffeault, J.-L. 2012 Using multiscale norms to quantify mixing and transport. Nonlinearity 25, 1–44.Google Scholar
Thiffeault, J.-L. & Pavliotis, G. A. 2008 Optimizing the source distribution in fluid mixing. Physica D 237, 918–929.Google Scholar
Vermach, L.2016 Using multiscale norms in nonlinear mixing optimisation. PhD thesis, University of Cambridge.Google Scholar
Vermach, L. & Caulfield, C. P. 2018 Optimal mixing in three-dimensional plane Poiseuille flow at high Péclet number. J. Fluid Mech. 850, 875–923.Google Scholar
Winters, K. B., Lombard, P. N., Riley, J. J. & Dasaro, E. A. 1995 Available potential energy and mixing in density-stratified fluids. J. Fluid Mech. 289, 115–128.Google Scholar

Marcotte et al. supplementary movie 1

Flow structure at Ri_b=0 in the time-averaged-kinetic-energy-optimal case (red scale: perturbation vorticity field, gray scale: density field)

Download Marcotte et al. supplementary movie 1(Video)
Video 5.2 MB

Marcotte et al. supplementary movie 2

Flow structure at Ri_b=0.05 in the time-averaged-kinetic-energy-optimal case (red scale: perturbation vorticity field, gray scale: density field)

Download Marcotte et al. supplementary movie 2(Video)
Video 3.5 MB

Marcotte et al. supplementary movie 3

Flow structure at Ri_b=0.1 in the time-averaged-kinetic-energy-optimal case (red scale: perturbation vorticity field, gray scale: density field)

Download Marcotte et al. supplementary movie 3(Video)
Video 4.8 MB

Marcotte et al. supplementary movie 4

Flow structure at Ri_b=0.2 in the time-averaged-kinetic-energy-optimal case (red scale: perturbation vorticity field, gray scale: density field)

Download Marcotte et al. supplementary movie 4(Video)
Video 3.5 MB

Marcotte et al. supplementary movie 5

Flow structure at Ri_b=0.5 in the time-integrated-kinetic-energy-optimal case (red scale: perturbation vorticity field, gray scale: density field)

Download Marcotte et al. supplementary movie 5(Video)
Video 3.4 MB

Marcotte et al. supplementary movie 6

Flow structure at Ri_b=1 in the time-integrated-kinetic-energy-optimal case (red scale: perturbation vorticity field, gray scale: density field)

Download Marcotte et al. supplementary movie 6(Video)
Video 3.3 MB

Marcotte et al. supplementary movie 7

Flow structure at Ri_b=0 in the mix-norm-optimal case (red scale: perturbation vorticity field, gray scale: density field)

Download Marcotte et al. supplementary movie 7(Video)
Video 5.3 MB

Marcotte et al. supplementary movie 8

Flow structure at Ri_b=0.05 in the mix-norm-optimal case (red scale: perturbation vorticity field, gray scale: density field)

Download Marcotte et al. supplementary movie 8(Video)
Video 5.3 MB

Marcotte et al. supplementary movie 9

Flow structure at Ri_b=0.1 in the mix-norm-optimal case (red scale: perturbation vorticity field, gray scale: density field)

Download Marcotte et al. supplementary movie 9(Video)
Video 2.2 MB

Marcotte et al. supplementary movie 10

Flow structure at Ri_b=0.25 in the mix-norm-optimal case (red scale: perturbation vorticity field, gray scale: density field)

Download Marcotte et al. supplementary movie 10(Video)
Video 5 MB

Marcotte et al. supplementary movie 11

Flow structure at Ri_b=0.5 in the mix-norm-optimal case (red scale: perturbation vorticity field, gray scale: density field)

Download Marcotte et al. supplementary movie 11(Video)
Video 5.2 MB

Marcotte et al. supplementary movie 12

Flow structure at Ri_b=1 in the mix-norm-optimal case (red scale: perturbation vorticity field, gray scale: density field)

Download Marcotte et al. supplementary movie 12(Video)
Video 5.1 MB