Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-18T03:19:06.118Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimal inflow boundary condition perturbations in steady stenotic flow

Published online by Cambridge University Press:  01 March 2012

X. Mao ,
H. M. Blackburn  and
S. J. Sherwin
X. Mao
Affiliation:
Department of Mechanical and Aerospace Engineering, Monash University, Vic 3800, Australia
H. M. Blackburn
Affiliation:
Department of Mechanical and Aerospace Engineering, Monash University, Vic 3800, Australia
S. J. Sherwin*
Affiliation:
Department of Aeronautics, Imperial College London, South Kensington SW7 2AZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We determine optimal inflow boundary perturbations to steady flow through a straight inflexible tube with a smooth axisymmetric stenosis at a bulk-flow Reynolds number 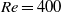, for which the flow is asymptotically stable. The perturbations computed produce an optimal gain, i.e. kinetic energy in the domain at a given time horizon normalized by a measure of time-integrated energy on the inflow boundary segment. We demonstrate that similarly to the optimal initial condition problem, the gain can be interpreted as the leading singular value of the forward linearized operator that evolves the boundary conditions to the final state at a fixed time. In this investigation we restrict our attention to problems where the temporal profile of the perturbations examined is a product of a Gaussian bell and a sinusoid, whose frequency is selected to excite axial wavelengths similar to those of the optimal initial perturbations in the same geometry. Comparison of the final state induced by the optimal boundary perturbation with that induced by the optimal initial condition demonstrates a close agreement for the selected problem. Previous works dealing with optimal boundary perturbation considered a prescribed spatial structure and computed an optimal temporal variation of a wall-normal velocity component, whereas in this paper we consider the problem of a prescribed temporal structure and compute the optimal spatial variation of velocity boundary conditions over a one-dimensional inflow boundary segment. The methodology is capable of optimizing boundary perturbations in general non-parallel two- and three-dimensional flows.

JFM classification

Instability: Absolute/convective instability Biological Fluid Dynamics: Blood flow
Type
Papers
Information
Journal of Fluid Mechanics , Volume 705: Special issue dedicated to Professor T. J. Pedley on his 70th birthday , 25 August 2012 , pp. 306 - 321
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Barkley, D., Blackburn, H. M. & Sherwin, S. J. 2008 Direct optimal growth analysis for timesteppers. Intl J. Numer. Meth. Fluids 57, 1437–1458.CrossRefGoogle Scholar
2. Barkley, D. & Henderson, R. D. 1996 Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241.CrossRefGoogle Scholar
3. Blackburn, H. M., Barkley, D. & Sherwin, S. J. 2008a Convective instability and transient growth in flow over a backward-facing step. J. Fluid Mech. 603, 271–304.CrossRefGoogle Scholar
4. Blackburn, H. M. & Sherwin, S. J. 2004 Formulation of a Galerkin spectral element–Fourier method for three-dimensional incompressible flows in cylindrical geometries. J. Comput. Phys. 197 (2), 759–778.Google Scholar
5. Blackburn, H. M. & Sherwin, S. J. 2007 Instability modes and transition of pulsatile stenotic flow: pulse-period dependence. J. Fluid Mech. 573, 57–88.CrossRefGoogle Scholar
6. Blackburn, H. M., Sherwin, S. J. & Barkley, D. 2008b Convective instability and transient growth in steady and pulsatile stenotic flows. J. Fluid Mech. 607, 267–277.CrossRefGoogle Scholar
7. Cantwell, C. D., Barkley, D. & Blackburn, H. M. 2010 Transient growth analysis of flow through a sudden expansion in a circular pipe. Phys. Fluids 22, 034101–1–15.Google Scholar
8. Chomaz, J.-M. 2005 Global instabilities in spatially developing flows: non-normality and nonlinearity. Annu. Rev. Fluid Mech. 37, 357–392.Google Scholar
9. Corbett, P. & Bottaro, A. 2001 Optimal control of nonmodal disturbance in boundary layers. Theor. Comput. Fluid Dyn. 15, 65–81.CrossRefGoogle Scholar
10. Guégan, A., Schmid, P. J. & Huerre, P. 2006 Optimal energy growth and optimal control in swept Hiemenz flow. J. Fluid Mech. 566, 11–45.CrossRefGoogle Scholar
11. Hogberg, M. & Henningson, D. S. 2002 Linear optimal control applied to instabilities in spatially developing boundary layers. J. Fluid Mech. 470, 151–179.CrossRefGoogle Scholar
12. Mao, X., Sherwin, S. J. & Blackburn, H. M. 2011 Transient growth and bypass transition in stenotic flow with a physiological waveform. Theor. Comput. Fluid Dyn. 25 (1), 31–42.CrossRefGoogle Scholar
13. Nocedal, J. & Wright, S. 1999 Numerical Optimization. Springer.Google Scholar
14. Schmid, P. J. 2007 Nonmodal stability theory. Annu. Rev. Fluid Mech. 39, 129–162.Google Scholar
15. Sherwin, S. J. & Blackburn, H. M. 2005 Three-dimensional instabilities and transition of steady and pulsatile flows in an axisymmetric stenotic tube. J. Fluid Mech. 533, 297–327.CrossRefGoogle Scholar