Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-05T12:03:38.808Z Has data issue: false hasContentIssue false
  • English
  • Français

The onset of vortex-induced vibrations of a flexible cylinder at large inclination angle

Published online by Cambridge University Press:  09 November 2016

Rémi Bourguet  and
Michael S. Triantafyllou
Rémi Bourguet*
Affiliation:
Institut de Mécanique des Fluides de Toulouse, Université de Toulouse and CNRS, Toulouse, 31400, France
Michael S. Triantafyllou
Affiliation:
Massachusetts Institute of Technology, Cambridge, MA 02139, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The onset of the vortex-induced vibration (VIV) regime of a flexible cylinder inclined at 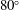$80^{\circ }$ within a uniform current is studied by means of direct numerical simulations, at Reynolds number 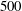$500$ based on the body diameter and inflow velocity magnitude. A range of values of the reduced velocity, defined as the inverse of the fundamental natural frequency, is examined in order to capture the emergence of the body responses and explore the concomitant reorganization of the flow and fluid forcing. Additional simulations at normal incidence confirm that the independence principle, which states that the system behaviour is determined by the normal inflow component, does not apply at such large inclination angle. Contrary to the normal incidence case, the free vibrations of the inclined cylinder arise far from the Strouhal frequency, i.e. the vortex shedding frequency downstream of a fixed rigid cylinder. The trace of the stationary body wake is found to persist beyond the vibration onset: the flow may still exhibit an oblique component that relates to the slanted vortex shedding pattern observed in the absence of vibration. This flow component which occurs close to the Strouhal frequency, at a high and incommensurable frequency compared to the vibration frequency, is referred to as Strouhal component; it induces a high-frequency component in fluid forcing. The vibration onset is accompanied by the appearance of novel, low-frequency components of the flow and fluid forcing which are synchronized with body motion. This second dominant flow component, referred to as lock-in component, is characterized by a parallel spatial pattern. The Strouhal and lock-in components of the flow coexist over a range of reduced velocities, with variable contributions, which results in a variety of mixed wake patterns. The transition from oblique to parallel vortex shedding that occurs during the amplification of the structural responses, is driven by the opposite trends of these two component contributions: the decrease of the Strouhal component magnitude associated with the progressive disappearance of the high-frequency force component, and simultaneously, the increase of the lock-in component magnitude, which dominates once the fully developed VIV regime is reached and the flow dynamics is entirely governed by wake–body synchronization.

JFM classification

Wakes/Jets: Vortex streets Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 809 , 25 December 2016 , pp. 111 - 134
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bearman, P. W. 1984 Vortex shedding from oscillating bluff bodies. Annu. Rev. Fluid Mech. 16, 195–222.CrossRefGoogle Scholar
Bearman, P. W. 2011 Circular cylinder wakes and vortex-induced vibrations. J. Fluids Struct. 27, 648–658.CrossRefGoogle Scholar
Benaroya, H. & Gabbai, R. D. 2008 Modelling vortex-induced fluid–structure interaction. Phil. Trans. R. Soc. Lond. A 366, 1231–1274.Google ScholarPubMed
Berkooz, G., Holmes, P. & Lumley, J. L. 1993 The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 25, 539–575.CrossRefGoogle Scholar
Blevins, R. D. 1990 Flow-induced Vibration. Van Nostrand Reinhold.Google Scholar
Bourguet, R., Braza, M. & Dervieux, A. 2007 Reduced-order modeling for unsteady transonic flows around an airfoil. Phys. Fluids 19, 111701.CrossRefGoogle Scholar
Bourguet, R., Karniadakis, G. E. & Triantafyllou, M. S. 2011a Vortex-induced vibrations of a long flexible cylinder in shear flow. J. Fluid Mech. 677, 342–382.CrossRefGoogle Scholar
Bourguet, R., Karniadakis, G. E. & Triantafyllou, M. S. 2013a Distributed lock-in drives broadband vortex-induced vibrations of a long flexible cylinder in shear flow. J. Fluid Mech. 717, 361–375.CrossRefGoogle Scholar
Bourguet, R., Karniadakis, G. E. & Triantafyllou, M. S. 2013b Multi-frequency vortex-induced vibrations of a long tensioned beam in linear and exponential shear flows. J. Fluids Struct. 41, 33–42.CrossRefGoogle Scholar
Bourguet, R., Karniadakis, G. E. & Triantafyllou, M. S. 2015 On the validity of the independence principle applied to the vortex-induced vibrations of a flexible cylinder inclined at 60° . J. Fluids Struct. 53, 58–69.CrossRefGoogle Scholar
Bourguet, R., Lucor, D. & Triantafyllou, M. S. 2012 Mono- and multi-frequency vortex-induced vibrations of a long tensioned beam in shear flow. J. Fluids Struct. 32, 52–64.CrossRefGoogle Scholar
Bourguet, R., Modarres-Sadeghi, Y., Karniadakis, G. E. & Triantafyllou, M. S. 2011b Wake-body resonance of long flexible structures is dominated by counter-clockwise orbits. Phys. Rev. Lett. 107, 134502.Google Scholar
Bourguet, R. & Triantafyllou, M. S. 2015 Vortex-induced vibrations of a flexible cylinder at large inclination angle. Phil. Trans. R. Soc. Lond. A 373, 20140108.Google ScholarPubMed
Cagney, N. & Balabani, S. 2014 Streamwise vortex-induced vibrations of cylinders with one and two degrees of freedom. J. Fluid Mech. 758, 702–727.CrossRefGoogle Scholar
Carberry, J., Sheridan, J. & Rockwell, D. 2005 Controlled oscillations of a cylinder: forces and wake modes. J. Fluid Mech. 538, 31–69.Google Scholar
Chaplin, J. R., Bearman, P. W., Huera-Huarte, F. J. & Pattenden, R. J. 2005 Laboratory measurements of vortex-induced vibrations of a vertical tension riser in a stepped current. J. Fluids Struct. 21, 3–24.CrossRefGoogle Scholar
Dahl, J. M., Hover, F. S., Triantafyllou, M. S. & Oakley, O. H. 2010 Dual resonance in vortex-induced vibrations at subcritical and supercritical Reynolds numbers. J. Fluid Mech. 643, 395–424.Google Scholar
Evangelinos, C. & Karniadakis, G. E. 1999 Dynamics and flow structures in the turbulent wake of rigid and flexible cylinders subject to vortex-induced vibrations. J. Fluid Mech. 400, 91–124.Google Scholar
Franzini, G. R., Gonçalves, R. T., Meneghini, J. R. & Fujarra, A. L. C. 2013 One and two degrees-of-freedom vortex-induced vibration experiments with yawed cylinders. J. Fluids Struct. 42, 401–420.CrossRefGoogle Scholar
Hover, F. S., Techet, A. H. & Triantafyllou, M. S. 1998 Forces on oscillating uniform and tapered cylinders in crossflow. J. Fluid Mech. 363, 97–114.CrossRefGoogle Scholar
Huera-Huarte, F. J. & Bearman, P. W. 2009 Wake structures and vortex-induced vibrations of a long flexible cylinder. Part 1: dynamic response. J. Fluids Struct. 25, 969–990.Google Scholar
Huera-Huarte, F. J. & Bearman, P. W. 2014 Towing tank experiments on the vortex-induced vibrations of low mass ratio long flexible cylinders. J. Fluids Struct. 48, 81–92.Google Scholar
Jain, A. & Modarres-Sadeghi, Y. 2013 Vortex-induced vibrations of a flexibly-mounted inclined cylinder. J. Fluids Struct. 43, 28–40.CrossRefGoogle Scholar
Karniadakis, G. E. & Sherwin, S. 1999 Spectral/hp Element Methods for CFD, 1st edn. Oxford University Press.Google Scholar
King, R. 1977 Vortex excited oscillations of yawed circular cylinders. Trans. ASME J. Fluids Engng 99, 495–502.CrossRefGoogle Scholar
King, R., Prosser, M. J. & Johns, D. J. 1973 On vortex excitation of model piles in water. J. Sound Vib. 29, 169–188.Google Scholar
Klamo, J. T., Leonard, A. & Roshko, A. 2006 The effects of damping on the amplitude and frequency response of a freely vibrating cylinder in cross-flow. J. Fluids Struct. 22, 845–856.Google Scholar
Konstantinidis, E. 2014 On the response and wake modes of a cylinder undergoing streamwise vortex-induced vibration. J. Fluids Struct. 45, 256–262.Google Scholar
Leontini, J. S., Thompson, M. C. & Hourigan, K. 2006 The beginning of branching behaviour of vortex-induced vibration during two-dimensional flow. J. Fluids Struct. 22, 857–864.Google Scholar
Lie, H. & Kaasen, K. E. 2006 Modal analysis of measurements from a large-scale VIV model test of a riser in linearly sheared flow. J. Fluids Struct. 22, 557–575.CrossRefGoogle Scholar
Lucor, D. & Karniadakis, G. E. 2003 Effects of oblique inflow in vortex-induced vibrations. Flow Turbul. Combust. 71, 375–389.Google Scholar
Lucor, D., Mukundan, H. & Triantafyllou, M. S. 2006 Riser modal identification in CFD and full-scale experiments. J. Fluids Struct. 22, 905–917.Google Scholar
Lucor, D. & Triantafyllou, M. S. 2008 Parametric study of a two degree-of-freedom cylinder subject to vortex-induced vibrations. J. Fluids Struct. 24, 1284–1293.CrossRefGoogle Scholar
Ma, X. & Karniadakis, G. E. 2002 Flow structure from an oscillating cylinder. Part 1. Mechanisms of phase shift and recovery in the near wake. J. Fluid Mech. 458, 181–190.Google Scholar
Mittal, S. & Tezduyar, T. E. 1992 A finite element study of incompressible flows past oscillating cylinders and aerofoils. Intl J. Numer. Meth. Fluids 15, 1073–1118.Google Scholar
Modarres-Sadeghi, Y., Chasparis, F., Triantafyllou, M. S., Tognarelli, M. & Beynet, P. 2011 Chaotic response is a generic feature of vortex-induced vibrations of flexible risers. J. Sound Vib. 330, 2565–2579.Google Scholar
Naudascher, E. 1987 Flow-induced streamwise vibrations of structures. J. Fluids Struct. 1, 265–298.Google Scholar
Naudascher, E. & Rockwell, D. 1994 Flow-induced Vibrations: An Engineering Guide. Dover.Google Scholar
Navrose & Mittal, S. 2013 Free vibrations of a cylinder: 3-D computations at Re = 1000. J. Fluids Struct. 41, 109–118.Google Scholar
Newman, D. J. & Karniadakis, G. E. 1997 A direct numerical simulation study of flow past a freely vibrating cable. J. Fluid Mech. 344, 95–136.CrossRefGoogle Scholar
Noack, B. R., Afanasiev, K., Morzynski, M., Tadmor, G. & Thiele, F. 2003 A hierarchy of low-dimensional models for the transient and post-transient cylinder wake. J. Fluid Mech. 497, 335–363.Google Scholar
Okajima, A., Kosugi, T. & Nakamura, A. 2002 Flow-induced in-line oscillation of a circular cylinder in a water tunnel. Trans. ASME J. Press. Vessel Technol. 124, 89–96.Google Scholar
Païdoussis, M. P., Price, S. J. & de Langre, E. 2010 Fluid-Structure Interactions: Cross-Flow-Induced Instabilities. Cambridge University Press.Google Scholar
Ramberg, S. E. 1983 The effects of yaw and finite length upon the vortex wakes of stationary and vibrating circular cylinders. J. Fluid Mech. 128, 81–107.CrossRefGoogle Scholar
Sarpkaya, T. 2004 A critical review of the intrinsic nature of vortex-induced vibrations. J. Fluids Struct. 19, 389–447.Google Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures. Part I–II. Q. Appl. Maths 45, 561–590.CrossRefGoogle Scholar
Thakur, A., Liu, X. & Marshall, J. S. 2004 Wake flow of single and multiple yawed cylinders. Trans. ASME J. Fluids Engng 126, 861–870.Google Scholar
Trim, A. D., Braaten, H., Lie, H. & Tognarelli, M. A. 2005 Experimental investigation of vortex-induced vibration of long marine risers. J. Fluids Struct. 21, 335–361.Google Scholar
Van Atta, C. W. 1968 Experiments on vortex shedding from yawed circular cylinders. AIAA J. 6, 931–933.Google Scholar
Vandiver, J. K., Jaiswal, V. & Jhingran, V. 2009 Insights on vortex-induced, traveling waves on long risers. J. Fluids Struct. 25, 641–653.CrossRefGoogle Scholar
Willden, R. H. J. & Guerbi, M. 2010 Vortex dynamics of stationary and oscillating cylinders in yawed flow. In IUTAM Symp. on Bluff Body Wakes and Vortex-Induced Vibrations (BBVIV-6), Capri, Italy, pp. 47–54.Google Scholar
Williamson, C. H. K. & Govardhan, R. 2004 Vortex-induced vibrations. Annu. Rev. Fluid Mech. 36, 413–455.Google Scholar
Zhao, M., Cheng, L. & Zhou, T. 2009 Direct numerical simulation of three-dimensional flow past a yawed circular cylinder of infinite length. J. Fluids Struct. 25, 831–847.CrossRefGoogle Scholar