Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-17T21:25:34.266Z Has data issue: false hasContentIssue false
  • English
  • Français

Onset of thin film meniscus along a fibre

Published online by Cambridge University Press:  22 February 2019

Shuo Guo ,
Xianmin Xu ,
Tiezheng Qian ,
Yana Di ,
Masao Doi  and
Penger Tong Open the ORCID record for Penger Tong [Opens in a new window]
Shuo Guo
Affiliation:
Department of Physics, Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong
Xianmin Xu
Affiliation:
LSEC, Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing 100190, China
Tiezheng Qian
Affiliation:
Department of Mathematics, Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong
Yana Di
Affiliation:
LSEC, Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing 100190, China
Masao Doi
Affiliation:
Interdisciplinary Research Center, Beihang University, Beijing 100191, China
Penger Tong*
Affiliation:
Department of Physics, Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The dynamics of spreading of a macroscopic liquid droplet over a wetting surface is often described by a power-law relaxation, namely, the droplet radius increases as 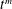$t^{m}$ for time $t$, which is known as Tanner’s law. Here we show, by both experiments and theory, that when the liquid spreading takes place between a thin soap film and a glass fibre penetrating the film, the spreading is significantly slowed down. When the film thickness 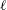$\ell$ becomes smaller than the fibre diameter 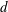$d$, the strong hydrodynamic confinement effect of the soap film gives rise to a logarithmic relaxation with fibre creeping time $t$. Such a slow dynamics of spreading is observed for hours both in the measured time-dependent height of capillary rise 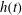$h(t)$ on the fibre surface and viscous friction coefficient 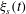$\unicode[STIX]{x1D709}_{s}(t)$ felt by the glass fibre in contact with the soap film. A new theoretical approach based on the Onsager variational principle is developed to describe the dynamics of thin film spreading along a fibre. The newly derived equations of motion provide the analytical solutions of 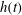$h(t)$ and contact angle 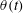$\unicode[STIX]{x1D703}(t)$, which are found to be in good agreement with the experimental results. Our work thus provides a common framework for understanding the confinement effect of thin soap films on the dynamics of spreading along a fibre.

JFM classification

Interfacial Flows (free surface): Capillary flows Interfacial Flows (free surface): Contact lines Interfacial Flows (free surface): Thin films
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 865 , 25 April 2019 , pp. 650 - 680
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bonn, D., Eggers, J., Indekeu, J., Meunier, J. & Rolley, E. 2009 Wetting and spreading. Rev. Mod. Phys. 81, 739–805.10.1103/RevModPhys.81.739Google Scholar
Clanet, C. & Quéré, D. 2002 Onset of menisci. J. Fluid Mech. 460, 131–149.10.1017/S002211200200808XGoogle Scholar
Decker, E. L. & Garoff, S. 1997 Contact angle hysteresis: the need for new theoretical and experimental models. J. Adhes. 63, 159–185.Google Scholar
de Gennes, P. G., Brochard-Wyart, F. & Quéré, D. 2004 Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves. Springer.10.1007/978-0-387-21656-0Google Scholar
de Gennes, P. G. 1985 Wetting: statics and dynamics. Rev. Mod. Phys. 57, 827–863.10.1103/RevModPhys.57.827Google Scholar
Di, Y., Xu, X. & Doi, M. 2016 Theoretical analysis for meniscus rise of a liquid contained between a flexible film and a solid wall. Europhys. Lett. 113, 36001.10.1209/0295-5075/113/36001Google Scholar
Doi, M. 2011 Onsager’s variational principle in soft matter. J. Phys.: Condens. Matter 23, 284118.Google Scholar
Doi, M. 2013 Soft Matter Physics. Oxfort University Press.10.1093/acprof:oso/9780199652952.001.0001Google Scholar
Doi, M. 2015 Onsager principle as a tool for approximation. Chin. Phys. B 24, 020505.Google Scholar
Dussan, E. B. V. & Davis, S. H. J. 1974 On the motion of a fluid–fluid interface along a solid surface. Fluid Mech. 65, 71–95.10.1017/S0022112074001261Google Scholar
Guan, D., Wang, Y. J., Charlaix, E. & Tong, P. 2016a Asymmetric and speed-dependent capillary force hysteresis and relaxation of a suddenly stopped moving contact line. Phys. Rev. Lett. 116, 066102.10.1103/PhysRevLett.116.066102Google Scholar
Guan, D., Wang, Y. J., Charlaix, E. & Tong, P. 2016b Simultaneous observation of asymmetric speed-dependent contact force hysteresis and slow relaxation of a suddenly stopped moving contact line. Phys. Rev. E 94, 042802.Google Scholar
Guo, S., Gao, M., Xiong, X., Wang, Y., Wang, X., Sheng, P. & Tong, P. 2013 Direct measurement of friction of a fluctuating contact line. Phys. Rev. Lett. 111, 026101.10.1103/PhysRevLett.111.026101Google Scholar
Guo, S., Lee, C. H., Sheng, P. & Tong, P. 2015 Measurement of contact-line dissipation in a nanometer-thin soap film. Phys. Rev. E 91, 012404.Google Scholar
Guo, S., Xiong, X., Xu, Z., Sheng, P. & Tong, P. 2014 Measurement of the friction coefficient of a fluctuating contact line using an AFM-based dual-mode mechanical resonator. Chin. Phys. B 23, 116802.Google Scholar
Huibers, P. D. T. & Shah, D. O. 1997 Multispectral determination of soap film thickness. Langmuir 13, 5995–5998.10.1021/la960738nGoogle Scholar
James, D. 1974 The meniscus on the outside of a small circular cylinder. J. Fluid Mech. 63 (4), 657–664.10.1017/S0022112074002126Google Scholar
Kaz, D. M., McGorty, R., Mani, M., Brenner, M. P. & Manoharan, V. N. 2012 Physical ageing of the contact line on colloidal particles at liquid interfaces. Nat. Mater. 11 (2), 138–142.10.1038/nmat3190Google Scholar
Landau, L. D. & Lifshitz, E. M. 1986 Fluid Mechanics, 2nd edn. Butterworth-Heinemann.Google Scholar
Leger, L. & Joanny, J.-F. 1992 Liquid spreading. Rep. Prog. Phys. 55, 431–486.10.1088/0034-4885/55/4/001Google Scholar
Lo, L. 1983 The meniscus on a needle – a lesson in matching. J. Fluid Mech. 132, 65–78.10.1017/S0022112083001470Google Scholar
Ma, H., Jimenez, J. & Rajagopalan, R. 2000 Brownian fluctuation spectroscopy using atomic force microscopes. Langmuir 16, 2254–2261.10.1021/la991059qGoogle Scholar
Man, X. & Doi, M. 2016 Ring to mountain transition in deposition pattern of drying droplets. Phys. Rev. Lett. 116, 066101.10.1103/PhysRevLett.116.066101Google Scholar
Pagonabarraga, I. 2012 Adsorbed colloids relax slowly. Nat. Mater. 11 (2), 99–100.10.1038/nmat3235Google Scholar
Poulin, P., Nallet, F., Cabane, B. & Bibette, J. 2015 Evidence for Newton black films between adhesive emulsion droplets. Phys. Rev. Lett. 77, 3248–3251.10.1103/PhysRevLett.77.3248Google Scholar
Quéré, D., Di Meglio, J. & Brochard-Wyart, F. 1988 Wetting of fibers: theory and experiments. Rev. Phys. Appl. 23, 1023–1030.10.1051/rphysap:019880023060102300Google Scholar
Quéré, D. 2008 Wetting and roughness. Annu. Rev. Mater. Res. 38, 71–99.10.1146/annurev.matsci.38.060407.132434Google Scholar
Ramiasa, M., Ralston, J., Fetzer, R. & Sedev, R. 2014 The influence of topography on dynamic wetting. Adv. Colloid Interface Sci. 206, 275–293.10.1016/j.cis.2013.04.005Google Scholar
Reif, F. 1985 Fundamentals of Statistical and Thermal Physics. McGraw-Hill.Google Scholar
Snoeijer, J. H. & Andreotti, B. 2013 Moving contact lines: scales, regimes, and dynamical transitions. Annu. Rev. Fluid Mech. 45, 269–292.10.1146/annurev-fluid-011212-140734Google Scholar
Tanner, L. H. 1979 The spreading of silicone oil drops on horizontal surfaces. J. Phys. D: Appl. Phys. 12, 1473–1484.10.1088/0022-3727/12/9/009Google Scholar
Wang, Y.-J., Guo, S., Chen, H.-Y. & Tong, P. 2016 Understanding contact angle hysteresis on an ambient solid surface. Phys. Rev. E 93, 052802.Google Scholar
Xiong, X., Guo, S., Xu, Z., Sheng, P. & Tong, P. 2009 Development of an atomic-force-microscope-based hanging-fiber rheometer for interfacial microrheology. Phys. Rev. E 80, 061604.Google Scholar
Xu, X., Di, Y. & Doi, M. 2016 Variational method for liquids moving on a substrate. Phys. Fluids 28, 087101.10.1063/1.4959227Google Scholar
Yazdanpanah, M. M., Hosseini, M., Pabba, S., Berry, S. M., Dobrokhotov, V. V., Safir, A., Keynton, R. S. & Cohn, R. W. 2008 Micro-Wilhelmy and related liquid property measurements using constant-diameter nanoneedle-tipped atomic force microscope probes. Langmuir 24, 13753–13764.10.1021/la802820uGoogle Scholar