Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kheirkhah, Sina
Cirtwill, J. D. Maxim
Saini, Pankaj
Venkatesan, Krishna
and
Steinberg, Adam M.
2017.
Dynamics and mechanisms of pressure, heat release rate, and fuel spray coupling during intermittent thermoacoustic oscillations in a model aeronautical combustor at elevated pressure.
Combustion and Flame,
Vol. 185,
Issue. ,
p.
319.
Mondal, S.
Pawar, S. A.
and
Sujith, R. I.
2017.
Synchronous behaviour of two interacting oscillatory systems undergoing quasiperiodic route to chaos.
Chaos: An Interdisciplinary Journal of Nonlinear Science,
Vol. 27,
Issue. 10,
Pawar, Samadhan A.
Seshadri, Akshay
Unni, Vishnu R.
and
Sujith, R. I.
2017.
Thermoacoustic instability as mutual synchronization between the acoustic field of the confinement and turbulent reactive flow.
Journal of Fluid Mechanics,
Vol. 827,
Issue. ,
p.
664.
Godavarthi, Vedasri
Pawar, Samadhan A.
Unni, Vishnu R.
Sujith, R. I.
Marwan, Norbert
and
Kurths, Jürgen
2018.
Coupled interaction between unsteady flame dynamics and acoustic field in a turbulent combustor.
Chaos: An Interdisciplinary Journal of Nonlinear Science,
Vol. 28,
Issue. 11,
p.
113111.
George, Nitin B.
Unni, Vishnu R.
Raghunathan, Manikandan
and
Sujith, R. I.
2018.
Pattern formation during transition from combustion noise to thermoacoustic instability via intermittency.
Journal of Fluid Mechanics,
Vol. 849,
Issue. ,
p.
615.
Pawar, Samadhan A.
Mondal, Sirshendu
George, Nitin Babu
and
Sujith, R I
2018.
Synchronization Behaviour During the Dynamical Transition in Swirl-Stabilized Combustor: Temporal and Spatiotemporal Analysis.
Unni, Vishnu R.
Krishnan, Abin
Manikandan, R.
George, Nitin B.
Sujith, R. I.
Marwan, Norbert
and
Kurths, Jürgen
2018.
On the emergence of critical regions at the onset of thermoacoustic instability in a turbulent combustor.
Chaos: An Interdisciplinary Journal of Nonlinear Science,
Vol. 28,
Issue. 6,
George, Nitin B
Unni, Vishnu R
Raghunathan, Manikandan
and
Sujith, R I
2018.
Suppression of thermoacoustic instability in a swirl-stabilized combustor by inducing blockage in the inlet flow stream.
Thomas, Nevin
Mondal, Sirshendu
Pawar, Samadhan A.
and
Sujith, R. I.
2018.
Effect of noise amplification during the transition to amplitude death in coupled thermoacoustic oscillators.
Chaos: An Interdisciplinary Journal of Nonlinear Science,
Vol. 28,
Issue. 9,
Juniper, Matthew P.
and
Sujith, R.I.
2018.
Sensitivity and Nonlinearity of Thermoacoustic Oscillations.
Annual Review of Fluid Mechanics,
Vol. 50,
Issue. 1,
p.
661.
Pawar, Samadhan A.
Sujith, Raman I.
Emerson, Benjamin
and
Lieuwen, Tim
2018.
Characterization of forced response of density stratified reacting wake.
Chaos: An Interdisciplinary Journal of Nonlinear Science,
Vol. 28,
Issue. 2,
Mondal, Sirshendu
Pawar, Samadhan A.
and
Sujith, R. I.
2018.
Energy for Propulsion.
p.
125.
George, Nitin B
Unni, Vishnu R
Raghunathan, Manikandan
and
Sujith, RI
2018.
Spatiotemporal dynamics during the transition to thermoacoustic instability: Effect of varying turbulence intensities.
International Journal of Spray and Combustion Dynamics,
Vol. 10,
Issue. 4,
p.
337.
Mondal, Sirshendu
Mukhopadhyay, Achintya
and
Sen, Swarnendu
2018.
Modeling and Simulation of Turbulent Combustion.
p.
543.
Schulz, Oliver
and
Noiray, Nicolas
2018.
Autoignition flame dynamics in sequential combustors.
Combustion and Flame,
Vol. 192,
Issue. ,
p.
86.
Dutta, Ankit Kumar
Ramachandran, Gopakumar
and
Chaudhuri, Swetaprovo
2019.
Investigating thermoacoustic instability mitigation dynamics with a Kuramoto model for flamelet oscillators.
Physical Review E,
Vol. 99,
Issue. 3,
Kasthuri, Praveen
Unni, Vishnu R.
and
Sujith, R. I.
2019.
Bursting and mixed mode oscillations during the transition to limit cycle oscillations in a matrix burner.
Chaos: An Interdisciplinary Journal of Nonlinear Science,
Vol. 29,
Issue. 4,
Guan, Yu
Li, Larry K. B.
Ahn, Byeonguk
and
Kim, Kyu Tae
2019.
Chaos, synchronization, and desynchronization in a liquid-fueled diffusion-flame combustor with an intrinsic hydrodynamic mode.
Chaos: An Interdisciplinary Journal of Nonlinear Science,
Vol. 29,
Issue. 5,
Kobayashi, Tsubasa
Murayama, Shogo
Hachijo, Takayoshi
and
Gotoda, Hiroshi
2019.
Early Detection of Thermoacoustic Combustion Instability Using a Methodology Combining Complex Networks and Machine Learning.
Physical Review Applied,
Vol. 11,
Issue. 6,
Manoj, Krishna
Pawar, Samadhan A.
Dange, Suraj
Mondal, Sirshendu
Sujith, R. I.
Surovyatkina, Elena
and
Kurths, Jürgen
2019.
Synchronization route to weak chimera in four candle-flame oscillators.
Physical Review E,
Vol. 100,
Issue. 6,
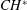 $CH^{\ast }$) images of the reaction zone. With a view to get an insight into this complex dynamics, we compute the instantaneous phases between acoustic pressure and local heat release rate oscillations. We observe that the aperiodic oscillations during combustion noise are phase asynchronous, while the large-amplitude periodic oscillations seen during thermoacoustic instability are phase synchronous. We find something interesting during intermittency: patches of synchronized periodic oscillations and desynchronized aperiodic oscillations coexist in the reaction zone. In other words, the emergence of order from disorder happens through a dynamical state wherein regions of order and disorder coexist, resembling a chimera state. Generally, mutually coupled chaotic oscillators synchronize but retain their dynamical nature; the same is true for coupled periodic oscillators. In contrast, during intermittency, we find that patches of desynchronized aperiodic oscillations turn into patches of synchronized periodic oscillations and vice versa. Therefore, the dynamics of local heat release rate oscillations change from aperiodic to periodic as they synchronize intermittently. The temporal variations in global synchrony, estimated through the Kuramoto order parameter, echoes the breathing nature of a chimera state.
$CH^{\ast }$) images of the reaction zone. With a view to get an insight into this complex dynamics, we compute the instantaneous phases between acoustic pressure and local heat release rate oscillations. We observe that the aperiodic oscillations during combustion noise are phase asynchronous, while the large-amplitude periodic oscillations seen during thermoacoustic instability are phase synchronous. We find something interesting during intermittency: patches of synchronized periodic oscillations and desynchronized aperiodic oscillations coexist in the reaction zone. In other words, the emergence of order from disorder happens through a dynamical state wherein regions of order and disorder coexist, resembling a chimera state. Generally, mutually coupled chaotic oscillators synchronize but retain their dynamical nature; the same is true for coupled periodic oscillators. In contrast, during intermittency, we find that patches of desynchronized aperiodic oscillations turn into patches of synchronized periodic oscillations and vice versa. Therefore, the dynamics of local heat release rate oscillations change from aperiodic to periodic as they synchronize intermittently. The temporal variations in global synchrony, estimated through the Kuramoto order parameter, echoes the breathing nature of a chimera state.