Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-22T20:15:07.663Z Has data issue: false hasContentIssue false
  • English
  • Français

The onset of dynamic stall at a high, transitional Reynolds number

Published online by Cambridge University Press:  28 December 2018

S. I. Benton Open the ORCID record for S. I. Benton [Opens in a new window]  and
M. R. Visbal
S. I. Benton*
Affiliation:
Air Force Research Laboratory, Wright-Patterson AFB, OH 45433, USA
M. R. Visbal
Affiliation:
Air Force Research Laboratory, Wright-Patterson AFB, OH 45433, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

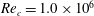Dynamic stall due to a ramp-type pitching motion is investigated on the NACA 0012 airfoil at chord Reynolds number of $Re_{c}=1.0\times 10^{6}$ through the use of wall-resolved large-eddy simulation. Emphasis is placed on the unsteady boundary-layer interactions that develop as the airfoil approaches stall. At this Reynolds number it is shown that turbulent separation moves upstream across much of the airfoil suction surface. When turbulent separation reaches the leading-edge separation bubble, a bursting event is initiated leading to a strong coherent leading-edge vortex structure. This vortex wraps up the turbulent shear layer to form a large dynamic stall vortex. The use of large-eddy simulation elucidates the roll of the laminar separation bubble in defining the onset of the dynamic stall process. Comparisons are made to identical simulations at lower Reynolds numbers of 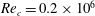$Re_{c}=0.2\times 10^{6}$ and 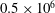$0.5\times 10^{6}$. This comparison demonstrates trends in the boundary-layer mechanics that explain the sensitivity of the dynamic stall process to Reynolds number.

JFM classification

Aerodynamics: Aerodynamics Boundary Layers: Boundary Layers Vortex Flows: Vortex Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 861 , 25 February 2019 , pp. 860 - 885
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alpert, P. 1981 Implicit filtering in conjunction with explicit filtering. J. Comput. Phys. 44 (1), 212–219.Google Scholar
Asada, K. & Kawai, S. 2018 Large-eddy simulation of airfoil flow near stall condition at Reynolds number 2. 1 × 106 . Phys. Fluids 30, 085103-22.Google Scholar
Beam, R. M. & Warming, R. F. 1978 An implicit factored scheme for the compressible Navier–Stokes equations. AIAA J. 16 (4), 393–402.Google Scholar
Benton, S. I. & Visbal, M. R. 2017 High-frequency forcing to delay dynamic stall at relevant Reynolds number. In 47th AIAA Fluid Dynamics Conference. American Institute of Aeronautics and Astronautics.Google Scholar
Carr, L. W. 1988 Progress in analysis and prediction of dynamic stall. J. Aircraft 25 (1), 6–17.Google Scholar
Carr, L. W., McAlister, K. W. & McCroskey, W. J.1977 Analysis of the development of dynamic stall based on oscillating airfoil experiments. Technical Note NASA TN D-8382. National Aeronautics and Space Administration.Google Scholar
Carr, L. W., McCroskey, W. J., McAlister, K. W., Pucci, S. L. & Lambert, O.1982 An experimental study of dynamic stall on advanced airfoil sections volume 3. Hot-wire and Hot-film measurements. NASA Technical Memorandum 84245. National Aeronautics and Space Administration.Google Scholar
Chandrasekhara, M. S., Carr, L. W. & Wilder, M. C. 1994 Interferometric investigations of compressible dynamic stall over a transiently pitching airfoil. AIAA J. 32 (3), 586–593.Google Scholar
Chandrasekhara, M. S., Wilder, M. C. & Carr, L. W. 1996 Boundary-layer-tripping studies of compressible dynamic stall flow. AIAA J. 34 (1), 96–103.Google Scholar
Critzos, C. C., Heyson, H. H. & Boswinkle, R. W. Jr 1955 Aerodynamic characteristics of NACA 0012 airfoil section at angles of attack from $0^{\circ }$ to $180^{\circ }$ . Technical Note 3361. National Advisory Committee for Aeronautics.Google Scholar
Diwan, S. S., Chetan, S. J. & Ramesh, O. N. 2006 On the bursting criterion for laminar separation bubbles. In Sixth IUTAM Symposium on Laminar-Turbulent Transition (ed. Govindarajan, R.), pp. 401–407. Springer.Google Scholar
Ekaterinaris, J. A. & Platzer, M. F. 1997 Computational prediction of airfoil dynamic stall. Prog. Aerosp. Sci. 33, 759–846.Google Scholar
Evans, W. T. & Mort, K. W.1959 Analysis of computed flow parameters for a set of sudden stalls in low-speed two-dimensional flow. Technical Note NASA TN D-85. National Aeronautics and Space Administration.Google Scholar
Gaitonde, D. V., Shang, J. S. & Young, J. L. 1999 Practical aspects of higher-order numerical schemes for wave propagation phenomena. Intl J. Numer. Meth. Engng 45, 1849–1869.Google Scholar
Gaitonde, D. V. & Visbal, M. R.1998 High-order schemes for Navier–Stokes equations: algorithm and implementation into FDL3DI. Final Report AFRL-VA-WP-TR-1998-3060. Air Force Research Laboratory.Google Scholar
Garmann, D. J., Visbal, M. R. & Orkwis, P. 2013 Comparative study of implicit and subgrid-scale model large-eddy simulation techniques for low-Reynolds number airfoil applications. Intl J. Numer. Meth. Fluids 71 (12), 1546–1565.Google Scholar
Georgiadis, N. J., Rizzetta, D. P. & Fureby, C. 2010 Large-eddy simulation: current capabilities, recommended practices, and future research. AIAA J. 48 (8), 1772–1784.Google Scholar
Gupta, R. & Ansell, P. J. 2018 Investigation of the effects of Reynolds number on the unsteady flow physics of airfoil dynamic stall. In 56th AIAA Aerospace Sciences Meeting. American Institute of Aeronautics and Astronautics.Google Scholar
Ham, N. D. 1967 Stall flutter of helicopter rotor blades: a special case of the dynamic stall phenomenon. J. Am. Helicopter Soc. 12 (4), 19–21.Google Scholar
Ham, N. D. 1972 Some recent mit research on dynamic stall. J. Aircraft 9 (5), 378–379.Google Scholar
Jones, B. M. 1934 Stalling. J. Roy. Aeronaut. Soc. 38 (285), 753–770.Google Scholar
Le Pape, A., Costes, M., Joubert, G., David, F. & Deluc, J. M. 2012 Dynamic stall control using deployable leading-edge vortex generators. AIAA J. 50 (10), 2135–2145.Google Scholar
Lee, T. & Gerontakos, P. 2004 Investigation of flow over an oscillating airfoil. J. Fluid Mech. 512, 313–341.Google Scholar
Leishman, J. G.1984 Contributions to the experimental investigation and analysis of aerofoil dynamic stall. PhD thesis, University of Glasgow.Google Scholar
Leishman, J. G. 1990 Dynamic stall experiments on the NACA 23012 aerofoil. Exp. Fluids 9, 49–58.Google Scholar
Lele, S. K. 1992 Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 103, 16–42.Google Scholar
Lorber, P. F. & Carta, F. O. 1988 Airfoil dynamic stall at constant pitch rate and high Reynolds number. J. Aircraft 25 (6), 548–556.Google Scholar
Martin, J. M., Empey, R. W., McCroskey, W. J. & Caradonna, F. X. 1974 An experimental analysis of dynamic stall on an oscillating airfoil. J. Am. Helicopter Soc. 19 (1), 26–32.Google Scholar
McAlister, K. W., Carr, L. W. & McCroskey, W. J.1978 Dynamic stall experiments on the naca 0012 airfoil. NASA Technical Paper 1100. National Aeronautics and Space Administration.Google Scholar
McAlister, K. W., Pucci, S. L., McCroskey, W. J. & Carr, L. W.1982 An experimental study of dynamic stall on advanced airfoil sections volume 2. Pressure and force data. NASA Technical Memorandum 84245. National Aeronautics and Space Administration.Google Scholar
McCroskey, W. J. 1982 Unsteady airfoils. Annu. Rev. Fluid Mech. 14, 285–311.Google Scholar
McCroskey, W. J., Carr, L. W. & McAlister, K. W. 1976 Dynamic stall experiments on oscillating airfoils. AIAA J. 14 (1), 57–63.Google Scholar
McCroskey, W. J., McAlister, K. W., Carr, L. W. & Pucci, S. L.1982 An experimental study of dynamic stall on advanced airfoil sections volume 1. Summary of the experiment. NASA Technical Memorandum 84245. National Aeronautics and Space Administration.Google Scholar
McCullough, G. B. & Gault, D. E.1951 Examples of three representative types of airfoil-section stall at low speed. Technical Note 2502. National Advisory Committee for Aeronautics.Google Scholar
Mulleners, K. & Raffel, M. 2012 The onset of dynamic stall revisited. Exp. Fluids 52, 779–793.Google Scholar
Mulleners, K. & Raffel, M. 2013 Dynamic stall development. Exp. Fluids 54, 1469-9.Google Scholar
Piomelli, U. & Balaras, E. 2002 Wall-layer models for large-eddy simulations. Annu. Rev. Fluid Mech. 34, 349–374.Google Scholar
Pruski, B. J. & Bowersox, R. D. W. 2013 Leading-edge flow structure of a dynamically pitching NACA 0012 airfoil. AIAA J. 51 (5), 1042–1053.Google Scholar
Richez, F., Mary, I., Gleize, V. & Basdevant, C. 2008 Near stall simulation of the flow around an airfoil using zonal rans/les coupling method. Comput. Fluids 37 (7), 857–866. Special Issue of the ‘Turbulence and Interaction-TI2006’ Conference.Google Scholar
Rizzetta, D. P., Visbal, M. R. & Blaisdell, G. A. 2003 A time-implicit high-order compact differencing and filtering scheme for large-eddy simulation. Intl J. Numer. Meth. Fluids 42 (6), 665–693.Google Scholar
Schreck, S. J., Faller, W. E. & Robinson, M. C. 2002 Unsteady separation processes and leading edge vortex precursors: pitch rate and Reynolds number influences. J. Aircraft 39 (5), 868–875.Google Scholar
Sheldahl, R. E. & Klimas, P. C.1981 Aerodynamic characteristics of seven symmetrical airfoil sections through 180-degree angle of attack for use in aerodynamic analysis of vertical axis wind turbines. Tech. Rep. SAND80-2114. Sandia National Laboratories.Google Scholar
Sherer, S. E. & Visbal, M. R. 2007 Multi-resolution implicit large eddy simulations using a high-order overset-grid approach. Intl J. Numer. Meth. Fluids 55 (5), 455–482.Google Scholar
Steger, J. L. 1978 Implicit finite-difference simulations of flow about arbitrary two-dimensional geometries. AIAA J. 16 (7), 679–686.Google Scholar
Tani, I. 1964 Low-speed flows involving bubble separations. Prog. Aerosp. Sci. 5, 70–103.Google Scholar
Vinokur, M. 1974 Conservation equations of gasdynamics in curvilinear coordinate systems. J. Comput. Phys. 14 (2), 105–125.Google Scholar
Visbal, M. R. 2014a Analysis of the Onset of Dynamic Stall Using High-fidelity Large-eddy Simulations. American Institute of Aeronautics and Astronautics.Google Scholar
Visbal, M. R. 2014b Numerical Exploration of Flow Control for Delay of Dynamic Stall on a Pitching Airfoil. American Institute of Aeronautics and Astronautics.Google Scholar
Visbal, M. R. 2015 Control of Dynamic Stall on a Pitching Airfoil Using High-frequency Actuation. American Institute of Aeronautics and Astronautics.Google Scholar
Visbal, M. R. & Gaitonde, D. V. 1999 High-order-accurate methods for complex unsteady subsonic flows. AIAA J. 37 (10), 1231–1239.Google Scholar
Visbal, M. R. & Gaitonde, D. V. 2002 On the use of higher-order finite-difference schemes on curvilinear and deforming meshes. J. Comput. Phys. 181, 155–185.Google Scholar
Visbal, M. R. & Garmann, D. J. 2017 Numerical investigation of spanwise end effects on dynamic stall of a pitching NACA 0012 wing. In 55th AIAA Aerospace Sciences Meeting. American Institute of Aeronautics and Astronautics.Google Scholar
Visbal, M. R. & Garmann, D. J. 2018 Analysis of dynamic stall on a pitching airfoil using high-fidelity large-eddy simulations. AIAA J. 56 (1), 46–63.Google Scholar
Visbal, M. R. & Rizzetta, D. P. 2002 Large-eddy simulation on curvilinear grids using compact differencing and filtering schemes. J. Fluids Engng 124, 836–847.Google Scholar
Visbal, M. R. & Shang, J. S. 1989 Investigation of the flow structure around a rapidly pitching airfoil. AIAA J. 27 (8), 1044–1051.Google Scholar
Wallis, R. A. 1962 Boundary-layer transition at the leading edge of thin wings and its effect on general nose separation. In Advances in Aeronautical Science, vol. 3. Pergamon Press.Google Scholar
Zhou, Y. & Wang, Z. J. 2010 Absorbing boundary conditions for the Euler and Navier–Stokes equations with the spectral difference method. J. Comput. Phys. 229 (23), 8733–8749.Google Scholar

Benton and Visbal supplementary movie

Contour of entropy visualizing the dynamic-stall process at z/c = 0.025 during the unsteady pitching motion. This movie animates the visualizations in Figures 5, 10, and 14 in the text.

Download Benton and Visbal supplementary movie(Video)
Video 6 MB