Article contents
On–off pumping for drag reduction in a turbulent channel flow
Published online by Cambridge University Press: 29 June 2023
Abstract
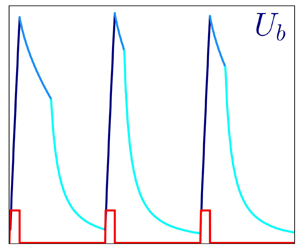
We show that the energy required by a turbulent flow to displace a given amount of fluid through a straight duct in a given time interval can be reduced by modulating in time the pumping power. The control strategy is hybrid: it is passive, as it requires neither a control system nor control energy, but it manipulates how pumping energy is delivered to the system (as in active techniques) to increase the pumping efficiency. Our control employs a temporally periodic pumping pattern, where a short and intense acceleration (in which the pumping system is on) followed by a longer deceleration (in which the pumping system is off) makes the flow alternately visit a quasi-laminar and a turbulent state. The computational study is for a plane channel flow, and employs direct numerical simulations, which present specific computational challenges, for example the highly varying instantaneous value of the Reynolds number, and the importance of discretisation effects. Particular care is devoted to a meaningful definition of drag reduction in the present context. The ability of the forcing to yield significant savings is demonstrated. Since only a small portion of the parameter space is investigated, the best performance of the control technique remains to be assessed.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 4
- Cited by



