Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Zaghi, S.
Muscari, R.
and
Mascio, A. Di
2016.
Assessment of blockage effects in wind tunnel testing of wind turbines.
Journal of Wind Engineering and Industrial Aerodynamics,
Vol. 154,
Issue. ,
p.
1.
Marrone, S.
Di Mascio, A.
and
Le Touzé, D.
2016.
Coupling of Smoothed Particle Hydrodynamics with Finite Volume method for free-surface flows.
Journal of Computational Physics,
Vol. 310,
Issue. ,
p.
161.
Xuliang, Yao
Lingwei, Meng
Feng, Wang
and
Xiaoli, Niu
2016.
Investigation of thrust and load characteristics of AUV propeller under the condition of different angle incoming flow.
p.
1.
Kumar, Praveen
and
Mahesh, Krishnan
2017.
Large eddy simulation of propeller wake instabilities.
Journal of Fluid Mechanics,
Vol. 814,
Issue. ,
p.
361.
Dubbioso, Giulio
Muscari, Roberto
Ortolani, Fabrizio
and
Di Mascio, Andrea
2017.
Analysis of propeller bearing loads by CFD. Part I: Straight ahead and steady turning maneuvers.
Ocean Engineering,
Vol. 130,
Issue. ,
p.
241.
Muscari, Roberto
Dubbioso, Giulio
and
Di Mascio, Andrea
2017.
Analysis of the flow field around a rudder in the wake of a simplified marine propeller.
Journal of Fluid Mechanics,
Vol. 814,
Issue. ,
p.
547.
Muscari, Roberto
Dubbioso, Giulio
Viviani, Michele
and
Di Mascio, Andrea
2017.
Analysis of the asymmetric behavior of propeller–rudder system of twin screw ships by CFD.
Ocean Engineering,
Vol. 143,
Issue. ,
p.
269.
Gong, Jie
Guo, Chun-yu
Zhao, Da-gang
Wu, Tie-cheng
and
Song, Ke-wei
2018.
A comparative DES study of wake vortex evolution for ducted and non-ducted propellers.
Ocean Engineering,
Vol. 160,
Issue. ,
p.
78.
Felli, M.
and
Falchi, M.
2018.
Propeller wake evolution mechanisms in oblique flow conditions.
Journal of Fluid Mechanics,
Vol. 845,
Issue. ,
p.
520.
Magionesi, Francesca
Dubbioso, Giulio
Muscari, Roberto
and
Di Mascio, Andrea
2018.
Modal analysis of the wake past a marine propeller.
Journal of Fluid Mechanics,
Vol. 855,
Issue. ,
p.
469.
Ortolani, Fabrizio
Dubbioso, Giulio
Muscari, Roberto
Mauro, Salvatore
and
Di Mascio, Andrea
2018.
Experimental and Numerical Investigation of Propeller Loads in Off-Design Conditions.
Journal of Marine Science and Engineering,
Vol. 6,
Issue. 2,
p.
45.
Chiron, L.
Marrone, S.
Di Mascio, A.
and
Le Touzé, D.
2018.
Coupled SPH–FV method with net vorticity and mass transfer.
Journal of Computational Physics,
Vol. 364,
Issue. ,
p.
111.
Wang, Lian-Zhou
Guo, Chun-Yu
Su, Yu-Min
and
Wu, Tie-Cheng
2018.
A numerical study on the correlation between the evolution of propeller trailing vortex wake and skew of propellers.
International Journal of Naval Architecture and Ocean Engineering,
Vol. 10,
Issue. 2,
p.
212.
Wang, Lianzhou
Guo, Chunyu
Xu, Pei
and
Su, Yumin
2018.
Analysis of the performance of an oscillating propeller in cavitating flow.
Ocean Engineering,
Vol. 164,
Issue. ,
p.
23.
Tan, Yue
Li, Jing
Li, Yuan
Liu, Chunbao
and
Koci, Jan
2019.
Improved Performance Prediction of Marine Propeller: Numerical Investigation and Experimental Verification.
Mathematical Problems in Engineering,
Vol. 2019,
Issue. 1,
Zhang, Qin
and
Jaiman, Rajeev K.
2019.
Numerical analysis on the wake dynamics of a ducted propeller.
Ocean Engineering,
Vol. 171,
Issue. ,
p.
202.
Hu, Jian
Zhang, Weipeng
Sun, Shili
and
Guo, Chunyu
2019.
Numerical simulation of Vortex–Rudder interactions behind the propeller.
Ocean Engineering,
Vol. 190,
Issue. ,
p.
106446.
Wang, Lianzhou
Guo, Chunyu
Xu, Pei
and
Su, Yumin
2019.
Analysis of the wake dynamics of a propeller operating before a rudder.
Ocean Engineering,
Vol. 188,
Issue. ,
p.
106250.
Guo, Hai-peng
Zou, Zao-jian
Wang, Feng
and
Liu, Yi
2019.
Numerical investigation on the hydrodynamic characteristics of a marine propeller operating in oblique inflow.
Applied Ocean Research,
Vol. 93,
Issue. ,
p.
101969.
Posa, Antonio
Broglia, Riccardo
Felli, Mario
Falchi, Massimo
and
Balaras, Elias
2019.
Characterization of the wake of a submarine propeller via Large-Eddy simulation.
Computers & Fluids,
Vol. 184,
Issue. ,
p.
138.
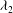 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\lambda _{2}$ criterion (Jeong & Hussain, J. Fluid Mech., vol. 285, 1995, pp. 69–94) and typical flow variables (pressure, velocity and vorticity), for both the averaged and instantaneous flow fields. Moreover, in order to further inspect the evolution of the vortical structures, as well as their interaction and destabilization, the spectra of the kinetic energy have been considered. This investigation aims to broaden the knowledge from previous works on the subject of rotor wake instabilities, focusing on the differences between an ideal (axisymmetric) and actual operating conditions occurring in typical engineering applications.
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\lambda _{2}$ criterion (Jeong & Hussain, J. Fluid Mech., vol. 285, 1995, pp. 69–94) and typical flow variables (pressure, velocity and vorticity), for both the averaged and instantaneous flow fields. Moreover, in order to further inspect the evolution of the vortical structures, as well as their interaction and destabilization, the spectra of the kinetic energy have been considered. This investigation aims to broaden the knowledge from previous works on the subject of rotor wake instabilities, focusing on the differences between an ideal (axisymmetric) and actual operating conditions occurring in typical engineering applications.

