Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-26T22:42:51.781Z Has data issue: false hasContentIssue false
  • English
  • Français

On the variety of particle accumulation structures under the effect of g-jitters

Published online by Cambridge University Press:  30 May 2013

Marcello Lappa
Marcello Lappa*
Affiliation:
Telespazio, via Gianturco 31, Napoli 80046, Italy
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The present analysis extends the author’s earlier work (Lappa, Phys. Fluids, vol. 25, 2003, 012101; Lappa, Chaos, vol. 23, 2003, 013105) on the properties of patterns formed by the spontaneous accumulation and ordering of solid particles in certain types of flow (with a toroidal structure and a travelling wave propagating in the azimuthal direction) by considering the potential impact of ‘vibrations’ (g-jitters) on such dynamics. It is shown that a kaleidoscope of possible variants exist whose nature and variety calls for a concerted analysis using the tools of computational fluid dynamics in synergy with dimensional arguments and existing theories on the effect of periodic accelerations on fluid systems. A possible categorization of the observed phenomena is introduced according to the type and scale of ‘defects’ displayed by the emerging particle aggregates with respect to unperturbed (vibration-less) conditions. 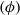It is shown that the resulting degree of ‘turbulence’ depends essentially on the direction $(\phi )$, amplitude 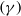$(\gamma )$ and frequency 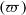$(\varpi )$ of the applied inertial disturbance. A range of amplitudes and frequencies exist where the formation of recognizable particle structures is prevented. A quantitative map (in the 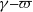$\gamma \text{{\ndash}} \varpi $ plane) for their occurrence is derived with the express intent of supporting the optimization of future experiments to be performed in space.

JFM classification

Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows Nonlinear Dynamical Systems: Nonlinear Dynamical Systems Nonlinear Dynamical Systems: Pattern formation
Type
Papers
Information
Journal of Fluid Mechanics , Volume 726 , 10 July 2013 , pp. 160 - 195
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahadi, A. H. & Saghir, M. Z. 2012 Quasi steady state effect of micro vibration from two space vehicles on mixture during thermodiffusion experiment. Fluid Dyn. Mater. Process. 8 (4), 397–422.Google Scholar
Alexander, J. I. D. 1990 Low gravity experiment sensitivity to residual acceleration: a review. Microgravity Sci. Tech. l (3), 52–68.Google Scholar
Atkinson, K. A. 1989 An Introduction to Numerical Analysis, 2nd ed. John Wiley & Sons.Google Scholar
Babiano, A., Cartwright, J. H. E., Piro, O. & Provenzale, A. 2000 Dynamics of a small neutrally buoyant sphere in a fluid and targeting in Hamiltonian systems. Phys. Rev. Lett. 84, 5764–5767.Google Scholar
Baird, M. H. I., Senior, M. G. & Thompson, R. J. 1967 Terminal velocities of spherical particles in a vertically oscillating liquid. Chem. Engng Sci. 22, 551–558.Google Scholar
Balboa Usabiaga, F., Pagonabarraga, I. & Delgado-Buscalioni, R. 2013 Inertial coupling for point particle fluctuating hydrodynamics. J. Comput. Phys. 235, 701–722.Google Scholar
Balkovsky, E., Falkovich, G. & Fouxon, A. 2001 Intermittent distribution of inertial particles in turbulent flows. Phys. Rev. Lett. 86, 2790–2793.CrossRefGoogle ScholarPubMed
Benczik, I. J., Toroczkai, Z. & Tél, T. 2002 Selective sensitivity of open chaotic flows on inertial tracer advection: catching particles with a stick. Phys. Rev. Lett. 89 (16), 164501.Google Scholar
Biringen, S. & Danabasoglu, G. 1990 Computation of convective flows with gravity modulation in rectangular cavities. J. Thermophys. 4, 357–365.CrossRefGoogle Scholar
Bothe, D., Kröger, M. & Warnecke, H.-J. 2011 A VOF-based conservative method for the simulation of reactive mass transfer from rising bubbles. Fluid Dyn. Mater. Process. 7 (3), 303–316.Google Scholar
Busse, F. H., Pfister, G. & Schwabe, D. 1998 Formation of dynamical structures in axisymmetric fluid systems. In Evolution of Spontaneous Structures in Dissipative Continuous Systems, Lecture Notes in Physics, vol. 55, pp. 86–126.Google Scholar
Carotenuto, L., Piccolo, C., Castagnolo, D., Lappa, M. & Garcìa-Ruiz, J. M. 2002 Experimental observations and numerical modelling of diffusion-driven crystallisation processes. Acta Cryst. D 58, 1628–1632.Google Scholar
Coimbra, C. F. M., L’Esperance, D. & Lambert, R. A. 2004 An experimental study on stationary history effects in high-frequency Stokes flows. J. Fluid Mech. 504, 353–363.CrossRefGoogle Scholar
Coimbra, F. M. & Rangel, R. H. 2001 Spherical particle motion in harmonic Stokes flows. AIAA J. 39 (9), 1673–1682.Google Scholar
Derksen, J. J. & Eskin, D. 2011 Flow-induced forces in agglomerates. Fluid Dyn. Mater. Process. 7 (4), 341–356.Google Scholar
Di Carlo, D., Edd, J. F., Humphry, K. J., Stone, H. A. & Toner, M. 2009 Particle segregation and dynamics in confined flows. Phys. Rev. Lett. 102, 094503.Google Scholar
Druzhinin, O. A. & Ostrovsky, L. A. 1994 The influence of basset force on particle dynamics in two dimensional flows. Physica D 76, 34–43.CrossRefGoogle Scholar
Dyko, M. P. & Vafai, K. 2007 Effects of gravity modulation on convection in a horizontal annulus. Intl J. Heat Mass Transfer 50, 348–360.Google Scholar
Ellison, J., Ahmadi, G., Regel, L. & Wilcox, W. 1995 Particle motion in a liquid under $g$ -jitter excitation. Microgravity Sci. Technol. 8, 140–147.Google Scholar
Esmaeeli, A. 2005 Phase distribution of bubbly flows under terrestrial and microgravity conditions. Fluid Dyn. Mater. Process. 1 (1), 63–80.Google Scholar
Esmaeeli, A. & Tryggvason, G. 1998 Direct numerical simulations of bubbly flows. Part I – low Reynolds number arrays. J. Fluid Mech. 377, 313–345.Google Scholar
Gershuni, G. Z., Lyubimov, D. V., Lyubimova, T. P. & Roux, B. 1994 Convective flows in a liquid bridge under the influence of high frequency vibrations. Microgravity Q. 4 (2), 113–122.Google Scholar
Gershuni, G. Z. & Zhukhovitskii, E. M. 1981 Convective instability of a fluid in a vibration field under conditions of weightlessness. Fluid Dyn. 16 (4), 498–504.Google Scholar
Gershuni, G. Z. & Zhukhovitskii, E. M. 1986 Vibrational thermal convection in zero gravity. Fluid. Mech. Sov. Res. 15 (1), 63–84.Google Scholar
Haller, G. & Sapsis, T. 2012 Lagrangian coherent structures and the smallest finite-time Lyapunov exponent. Chaos 21 (2), 023115.Google Scholar
Hassan, S. & Kawaji, M. 2008 The effects of vibrations on particle motion in a viscous fluid cell. J. Appl. Mech. 75, 031012.CrossRefGoogle Scholar
Hassan, S., Lyubimova, T. P., Lyubimov, D. V. & Kawaji, M. 2006a Motion of a sphere suspended in a vibrating liquid-filled container. J. Appl. Mech. 73, 72–78.Google Scholar
Hassan, S., Lyubimova, T. P., Lyubimov, D. V. & Kawaji, M. 2006b Effects of vibrations on particle motion near a wall: existence of attraction force. Intl J. Multiphase Flow 32 (9), 1037–1054.Google Scholar
Herringe, R. A. 1977 A study of particle motion induced by two-dimensional liquid oscillations. Intl J. Multiphase Flow 3 (3), 243–253.Google Scholar
Hirata, K., Sasaki, T. & Tanigawa, H. 2001 Vibrational effects on convection in a square cavity at zero gravity. J. Fluid Mech. 445, 327–344.CrossRefGoogle Scholar
Hjelmfelt, A. T. & Mockros, L. F. 1966 Motion of discrete particles in a turbulent fluid. Appl. Sci. Res. 16 (1), 149–161.Google Scholar
Homma, S., Yokotsuka, M., Tanaka, T., Moriguchi, K., Koga, J. & Tryggvason, G. 2011 Numerical simulation of an axisymmetric compound droplet by three-fluid front-tracking method. Fluid Dyn. Mater. Process. 7 (3), 231–240.Google Scholar
Houghton, G. 1961 The behaviour of particles in a sinusoidal vector field. Proc. R. Soc. A 272, 33–43.Google Scholar
Ikeda, S. 1989 Fall velocity of single spheres in vertically oscillating fluids. Fluid Dyn. Res. 5, 203–216.Google Scholar
Kamotani, Y., Prasad, A. & Ostrach, S. 1981 Thermal convection in an enclosure due to vibrations aboard spacecraft. AIAA J. 19, 511–516.Google Scholar
Kleckner, D. & Irvine, W. T. M. 2013 Creation and dynamics of knotted vortices. Nature Phys. doi:10.1038/nphys2560.Google Scholar
Kozlov, V. G., Ivanova, A. A. & Evesque, P. 2006 Block stratification of sedimenting granular matter in a vessel due to vertical vibration. Fluid Dyn. Mater. Process. 2 (3), 203–210.Google Scholar
Kuhlmann, H. C. & Muldoon, F. H. 2012 Understanding particle accumulation structures (PAS) in thermocapillary liquid bridges. JASMA 29 (2), 64–98.Google Scholar
Langbein, D. 1991 Motion of ensembles of spherical particles in a fluid due to $g$ -jitter. Adv. Space Res. 11 (7), 189–196.Google Scholar
Lappa, M. 2003a Three-dimensional numerical simulation of Marangoni flow instabilities in floating zones laterally heated by an equatorial ring. Phys. Fluids 15 (3), 776–789.CrossRefGoogle Scholar
Lappa, M. 2003b Growth and mutual interference of protein seeds under reduced gravity conditions. Phys. Fluids 15 (4), 1046–1057.Google Scholar
Lappa, M. 2004 Combined effect of volume and gravity on the three-dimensional flow instability in non-cylindrical floating zones heated by an equatorial ring. Phys. Fluids 16 (2), 331–343.Google Scholar
Lappa, M. 2005 Assessment of VOF strategies for the analysis of Marangoni migration, collisional coagulation of droplets and thermal wake effects in metal alloys under microgravity conditions. Comput. Mater. Continua 2 (1), 51–64.Google Scholar
Lappa, M. 2006 Oscillatory convective structures and solutal jets originated from discrete distributions of droplets in organic alloys with a miscibility gap. Phys. Fluids 18 (4), 042105.Google Scholar
Lappa, M. 2010 Thermal Convection: Patterns, Evolution and Stability. John Wiley & Sons.Google Scholar
Lappa, M. 2012 Rotating Thermal Flows in Natural and Industrial Processes. John Wiley & Sons.Google Scholar
Lappa, M. 2011 A theoretical and numerical multiscale framework for the analysis of pattern formation in protein crystal engineering. Intl J. Multiscale Comput. Engng 9 (2), 149–174.Google Scholar
Lappa, M. 2013a Assessment of the role of axial vorticity in the formation of article accumulation structures in supercritical Marangoni and hybrid thermocapillary-rotation-driven flows. Phys. Fluids 25 (1), 012101.Google Scholar
Lappa, M. 2013b On the existence and multiplicity of one-dimensional solid particle attractors in time-dependent Rayleigh–Bénard convection. Chaos 23 (1), 013105.Google Scholar
Lappa, M. & Carotenuto, L. 2003 Effect of convective disturbances induced by g-jitter on the periodic precipitation of lysozyme. Microgravity Sci. Technol. 14 (2), 41–56.Google Scholar
Lappa, M., Castagnolo, D. & Carotenuto, L. 2002 Sensitivity of the non-linear dynamics of lysozyme ‘Liesegang rings’ to small asymmetries. Physica A 314 (1–4), 623–635.Google Scholar
Lappa, M. & Piccolo, C. 2004 Higher modes of mixed buoyant-Marangoni unstable convection originated from a droplet dissolving in a liquid/liquid system with miscibility gap. Phys. Fluids 16 (12), 4262–4272.Google Scholar
Lappa, M., Piccolo, C. & Carotenuto, L. 2004 Mixed buoyant-Marangoni convection due to dissolution of a droplet in a liquid–liquid system with miscibility gap. Eur. J. Mech. (B/Fluids) 23 (5), 781–794.Google Scholar
Lappa, M. & Savino, R. 1999 Parallel solution of the 3D Marangoni flow instabilities in liquid bridges. Intl J. Numer. Meth. Fluids 31 (8), 911–925.Google Scholar
Lappa, M. & Savino, R. 2002 3D analysis of crystal/melt interface shape and Marangoni flow instability in solidifying liquid bridges. J. Comput. Phys. 180 (2), 751–774.Google Scholar
Lappa, M., Savino, R. & Monti, R. 2000 Influence of buoyancy forces on Marangoni flow instabilities in liquid bridges. Intl J. Numer. Meth. Heat Fluid Flow 10 (7), 721–749.Google Scholar
Lappa, M., Yasushiro, S. & Imaishi, N. 2003 3D numerical simulation of on ground Marangoni flow instabilities in liquid bridges of low Prandtl number fluid. Intl J. Numer. Meth. Heat Fluid Flow 13 (3), 309–340.Google Scholar
Lighthill, M. J. 1954 The response of laminar skin friction and heat transfer to fluctuations in the stream velocity. Proc. R. Soc. Lond. Ser. A 224, 1–23.Google Scholar
Lizée, A. & Alexander, J. I. D. 1997 Chaotic thermovibrational flow in a laterally heated cavity. Phys. Rev. E 56, 4152–4156.CrossRefGoogle Scholar
Mark, A., Rundqvist, R. & Edelvik, F. 2011 Comparison between different immersed boundary conditions for simulation of complex fluid flows. Fluid Dyn. Mater. Process. 7 (3), 241–258.Google Scholar
Maxey, M. R., Patel, B. K., Chang, E. J. & Wang, L.-P. 1997 Simulations of dispersed turbulent multiphase flow. Fluid Dyn. Res. 20 (1–6), 143–156.Google Scholar
Maxey, M. R. & Riley, J. J. 1983 Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids 26, 883–889.Google Scholar
Mei, R., Lawrence, J. & Adrian, J. 1991 Unsteady drag on a sphere at finite Reynolds number with small fluctuations in the free-stream velocity. J. Fluid Mech. 233, 613–631.CrossRefGoogle Scholar
Melnikov, D., Pushkin, D. & Shevtsova, V. 2011 Accumulation of particles in time-dependent thermocapillary flow in a liquid bridge. Modeling of experiments. Eur. Phys. J. Special Topics 192, 29–39.Google Scholar
Michaelides, E. E. 1997 Review – the transient equation of motion for particles, bubbles, and droplets. J. Fluids Engng 119, 233–247.Google Scholar
Monti, R., Savino, R. & Lappa, M. 1998 Microgravity sensitivity of typical fluid physics experiment, presented at the 17th Microgravity Measurements Group Meeting, Cleveland, Ohio, 24–26 March 1998, published in the Meeting Proceedings in NASA CP-1998-208414, 23, pp. 1–15 (ISSN: 0191-7811).Google Scholar
Monti, R., Savino, R. & Lappa, M. 2001 On the convective disturbances induced by g-jitter on the space station. Acta Astron. 48 (5–12), 603–615.CrossRefGoogle Scholar
Parsa, A. & Saghir, M. Z. 2012 Fluid flow behavior of a binary mixture under the influence of external disturbances using different density models. Fluid Dyn. Mater. Process. 8 (1), 27–50.Google Scholar
Pasquero, C., Provenzale, A. & Spiegel, E. A. 2003 Suspension and fall of heavy particles in random two-dimensional flow. Phys. Rev. Lett. 91, 054502.Google Scholar
Pushkin, D., Melnikov, D. & Shevtsova, V. 2011 Ordering of small particles in one-dimensional coherent structures by time-periodic flows. Phys. Rev. Lett. 106, 234501.Google Scholar
Raju, N. & Meiburg, E. 1995 The accumulation and dispersion of heavy particles in forced two-dimensional mixing layers. Part 2: the effect of gravity. Phys. Fluids 7, 1241–1264.CrossRefGoogle Scholar
Sapsis, T. & Haller, G. 2010 Clustering criterion for inertial particles in two-dimensional time-periodic and three-dimensional steady flows. Chaos 20, 017515.CrossRefGoogle ScholarPubMed
Savino, R. & Lappa, M. 2003 Assessment of the thermovibrational theory: application to $g$ -jitter on the Space Station. J. Spacecr. Rockets 40 (2), 201–210.Google Scholar
Savino, R., Paterna, D. & Lappa, M. 2003 Marangoni flotation of liquid droplets. J. Fluid Mech. 479, 307–326.CrossRefGoogle Scholar
Saw, E. W., Shaw, R. A., Ayyalasomayajula, S., Chuang, P. Y. & Gylfason, A. 2008 Inertial clustering of particles in high-Reynolds-number turbulence. Phys. Rev. Lett. 100, 214501.Google Scholar
Schwabe, D. & Mizev, A. I. 2011 Particles of different density in thermocapillary liquid bridges under the action of travelling and standing hydrothermal waves. Eur. Phys. J. Special Topics 192, 13–27.Google Scholar
Schwabe, D., Mizev, A. I., Tanaka, S. & Kawamura, H. 2006 Particle accumulation structures in time-dependent thermocapillary flow in a liquid bridge under microgravity. Microgravity Sci. Technol. 18 (3–4), 117–127.Google Scholar
Schwabe, D., Mizev, A. I., Udhayasankar, M. & Tanaka, S. 2007 Formation of dynamic particle accumulation structures in oscillatory thermocapillary flow in liquid bridges. Phys. Fluids 19 (7), 072102.Google Scholar
Shevtsova, V., Gaponenko, Y. A. & Nepomnyashchy, A. 2013 Thermocapillary flow regimes and instability caused by a gas stream along the interface. J. Fluid Mech. 714, 644–670.Google Scholar
Shevtsova, V., Kuhlmann, H., Montanero, J. M., Nepomnyaschy, A., Lappa, M., Schwabe, D., Matsumoto, S., Nishino, K., Ueno, I. & Yoda, S. 2008 Preparation of Space experiment in the FPEF facility: heat transfer at the interface in the systems with cylindrical symmetry, 26th International Symposium on Space Technology and Science, 1–8 June 2008, Hamamatsu City (ISTS Proceedings).Google Scholar
Shevtsova, V., Mialdun, A., Kawamura, H., Ueno, I., Nishino, K. & Lappa, M. 2011 Onset of hydrothermal instability in liquid bridge. Experimental benchmark. Fluid Dyn. Mater. Process. 7 (1), 1–28.Google Scholar
Simic-Stefani, S., Kawaji, M. & Hu, H. 2006 G-jitter induced motion of a protein crystal under microgravity. J. Cryst. Growth 294, 373–384.Google Scholar
Srinivasan, S. & Saghir, M. Z. 2011 Impact of the vibrations on soret separation in binary and ternary mixtures. Fluid Dyn. Mater. Process. 7 (2), 201–216.Google Scholar
Sun, J., Carlson, F. M., Regel, L. L., Wilcox, W. R., Lal, R. B. & Trolinger, J. D. 1994 Particle motion in the fluid experiment system in microgravity. Acta Astron. 34, 261–269.CrossRefGoogle Scholar
Tanaka, S., Kawamura, H., Ueno, I. & Schwabe, D. 2006 Flow structure and dynamic particle accumulation in thermocapillary convection in a liquid bridge. Phys. Fluids 18, 067103.CrossRefGoogle Scholar
Thomson, J. R., Casademunt, J., Drolet, F. & Vinals, J. 1997 Coarsening of solid–liquid mixtures in a random acceleration field. Phys. Fluids 9 (5), 1336–1343.Google Scholar
Tunstall, E. B. & Houghton, G. 1968 Retardation of falling spheres by hydrodynamic oscillations. Chem. Engng Sci. 23, 1067–1081.Google Scholar
Uchiyama, T. 2011 Grid-free vortex method for particle-laden gas flow. Fluid Dyn. Mater. Process. 7 (4), 371–388.Google Scholar
Ueno, I., Abe, Y., Noguchi, K. & Kawamura, H. 2008 Dynamic particle accumulation structure (PAS) in half-zone liquid bridge – reconstruction of particle motion by 3-D PTV. Adv. Space Res. 41 (12), 2145–2149.CrossRefGoogle Scholar
Ueno, I., Ono, Y., Nagano, D., Tanaka, S. & Kawamura, H. 2000 Modal oscillatory structure and dynamic particle accumulation in liquid-bridge Marangoni convection, in ‘4th JSME–KSME Thermal Engineering Conference’, JSME, Kobe, Japan.Google Scholar
Vojir, D. J. & Michaelides, E. E. 1994 The effect of the history term on the motion of rigid spheres in a viscous fluid. Intl J. Multiphase Flow 20, 547–556.Google Scholar
Yan, Y., Jules, K. & Saghir, M. Z. 2007 Comparative study of g-jitter effect on thermal diffusion aboard the international space station. Fluid Dyn. Mater. Process. 3 (3), 231–246.Google Scholar
Yan, Y., Shevtsova, V. & Saghir, M. Z. 2005 Numerical study of low frequency g-jitter effect on thermal diffusion. Fluid Dyn. Mater. Process. 1 (4), 315–328.Google Scholar
Zaichik, L., Alipchenkov, V. M. & Sinaiski, E. G. 2008 Particles in Turbulent Flows. Wiley-VCH Verlag GmbH & Co. KGaA.Google Scholar
Zinchenko, A. Z. 1994 An efficient algorithm for calculating multiparticle thermal interaction in a concentrated dispersion of spheres. J. Comput. Phys. 111, 120–134.Google Scholar
Zohdi, T. I. 2007 An Introduction to Modeling and Simulation of Particulate Flows. SIAM.CrossRefGoogle Scholar