Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-25T22:55:46.991Z Has data issue: false hasContentIssue false
  • English
  • Français

On the use of transpiration patterns for reduction of pressure losses

Published online by Cambridge University Press:  19 March 2021

Longyin Jiao  and
J.M. Floryan Open the ORCID record for J.M. Floryan [Opens in a new window]
Longyin Jiao
Affiliation:
School of Aerospace Engineering, Beijing Institute of Technology, Beijing100081, PR China
J.M. Floryan*
Affiliation:
Department of Mechanical and Materials Engineering, The University of Western Ontario, London, OntarioN6A 5B9, Canada
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

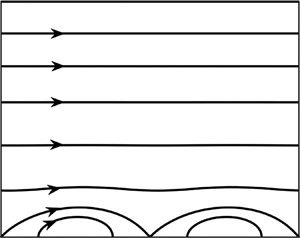
Pressure losses in laminar, pressure-gradient-driven channel flows modified by wall transpiration have been analysed in the range of Reynolds numbers guaranteeing flow stability. It was found that these losses were affected by the reduction of the effective channel opening due to formation of transpiration ‘bubbles’, by nonlinear streaming and by the elimination of direct contact between the stream and the bounding walls. It was further found that pressure losses can be reduced by properly selecting the transpiration pattern. It was determined that nonlinear streaming is the dominant effect as the transpiration wave number resulting in the largest reduction of pressure losses corresponds to the maximization of this streaming. Using transpiration at both walls further decreases pressure losses, but only when both transpiration patterns are in a proper relative position. The largest reduction of losses is achieved by concentrating transpiration at a single wave number. It is shown that the performance of finite-slot transpiration is well captured using just a few leading modes from the Fourier expansions describing the transpiration distribution. The analysis of energy expenditure shows that the use of transpiration increases the energy cost of the flow. Conditions leading to the minimization of this cost represent the most effective use of transpiration as a propulsion augmentation system.

JFM classification

Flow Control: Drag reduction
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 915 , 25 May 2021 , A78
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abtahi, A. & Floryan, J.M. 2017 Natural convection and thermal drift. J. Fluid Mech. 826, 553–582.CrossRefGoogle Scholar
Aljallis, E., Sarshar, M.A., Datla, R., Sikka, V., Jones, A. & Choi, C.H. 2013 Experimental study of skin friction drag reduction on superhydrophobic flat plates in high Reynolds number boundary layer flow. Phys. Fluids 25, 025103.CrossRefGoogle Scholar
Arnal, D., Perraud, J. & Séraudie, A. 2008 Attachment line and surface imperfection problems. In Advances in Laminar–Turbulent transition Modeling, RTO-EN-AVT-151, Brussels, Belgium.Google Scholar
Bewley, T.R. 2009 A fundamental limit on the balance of power in a transpiration-controlled channel flow. J. Fluid Mech. 632, 443–446.CrossRefGoogle Scholar
Bewley, T.R. & Alamo, O.M. 2004 A ‘win–win’ mechanism for low-drag transients in controlled two-dimensional channel flow and its implications for sustained drag reduction. J. Fluid Mech. 499, 183–196.CrossRefGoogle Scholar
Bocquet, L. & Lauga, E. 2011 A smooth future? Nat. Mater. 10, 334–337.CrossRefGoogle ScholarPubMed
Byrd, R.H., Gilbert, J.C. & Nocedal, J. 2000 A trust region method based on interior point techniques for nonlinear programming. Math. Program. Ser. A 89, 149–185.CrossRefGoogle Scholar
Byrd, R.H., Hribar, M.E. & Nocedal, J. 1999 An interior point algorithm for large-scale nonlinear programming. SIAM J. Optim. 9, 877–900.CrossRefGoogle Scholar
Canuto, C., Hussaini, M.Y., Quarteroni, A. & Zang, T.A. 1996 Spectral Methods. Springer.Google Scholar
Chen, Y., Floryan, J.M., Chew, Y.T. & Khoo, B.C. 2016 Groove-induced changes of discharge in channel flows. J. Fluid Mech. 799, 297–333.CrossRefGoogle Scholar
Coleman, T.F. & Li, Y. 1994 On the convergence of interior-reflective Newton method for nonlinear minimization subject to bounds. Math. Program. 67, 189–222.CrossRefGoogle Scholar
Coleman, T.F. & Li, Y. 1996 An interior trust region approach for nonlinear minimization subject to bounds. SIAM J. Optim. 6, 418–445.CrossRefGoogle Scholar
DeGroot, C.T., Wang, C. & Floryan, J.M. 2016 Drag reduction due to streamwise grooves in turbulent channel flow. ASME J. Fluid Engng 138, 1–10.CrossRefGoogle Scholar
Floryan, J.M. 1997 Stability of wall bounded shear layers with simulated distributed surface roughness. J. Fluid Mech. 335, 29–55.CrossRefGoogle Scholar
Floryan, J.M. 2003 Wall-transpiration-induced instabilities in plane Couette flow. J. Fluid Mech. 488, 151–188.CrossRefGoogle Scholar
Floryan, D. & Floryan, J.M. 2015 Drag reduction in heated channels. J. Fluid Mech. 765, 353–395.CrossRefGoogle Scholar
Floryan, J.M., Yamamoto, K. & Murase, T. 1992 Laminar-turbulent transition in plane Poiseuille flow in the presence of simulated wall roughness. CASI J. 38, 173–182.Google Scholar
Floryan, J.M. & Zandi, S. 2019 Reduction of pressure losses and increase of mixing in laminar flows through channels with long-wavelength vibrations. J. Fluid Mech. 864, 670–707.CrossRefGoogle Scholar
Fukagata, K., Sugiyama, K. & Kasagi, N. 2009 On the lower bound of net driving power in controlled duct flows. Physica D 238, 1082–1086.CrossRefGoogle Scholar
Fukunishi, Y. & Ebina, I. 2001 Active control of boundary-layer transition using a thin actuator. JSME Intl J. 44, 24–29.CrossRefGoogle Scholar
Gepner, S.W. & Floryan, J.M. 2020 Use of surface corrugations for energy-efficient chaotic stirring in low Reynolds number flows. Sci. Rep. 10 (1), 1–8.CrossRefGoogle ScholarPubMed
Gomez, F., Blackburn, H., Rudman, M., Sharma, A. & McKeon, B. 2016 Streamwise-varying steady transpiration control in turbulent pipe flow. J. Fluid Mech. 796, 588–616.CrossRefGoogle Scholar
Hœpffner, J. & Fukagata, K. 2009 Pumping or drag reduction? J. Fluid Mech. 635, 171–187.CrossRefGoogle Scholar
Hossain, M.Z. & Floryan, J.M. 2014 Natural convection in a fluid layer periodically heated from above. Phys. Rev. E 90, 023015.CrossRefGoogle Scholar
Hossain, M.Z. & Floryan, J.M. 2015 Natural convection in a horizontal fluid layer periodically heated from above and below. Phys. Rev. E 92, 023015.CrossRefGoogle Scholar
Hossain, M.Z. & Floryan, J.M. 2016 Drag reduction in a thermally modulated channel. J. Fluid Mech. 791, 122–153.CrossRefGoogle Scholar
Hossain, M.Z. & Floryan, J.M. 2020 On the role of surface grooves in the reduction of pressure losses in heated channels. Phys. Fluids 32, 083610.CrossRefGoogle Scholar
Hossain, M.Z., Floryan, D. & Floryan, J.M. 2012 Drag reduction due to spatial thermal modulations. J. Fluid Mech. 713, 398–419.CrossRefGoogle Scholar
Inasawa, A., Ninomiya, C. & Asai, M. 2013 Suppression of tonal trailing-edge noise from an airfoil using a plasma actuator. AIAA J. 51, 1695–1702.CrossRefGoogle Scholar
Kato, T., Fukunishi, Y. & Kobayashi, R. 1997 Artificial control of the three-dimensionalization process of T-S waves in boundary-layer transition. JSME Intl J. 40, 536–541.CrossRefGoogle Scholar
Koganezawa, S., Mitsuishi, A., Shimura, T., Iwamoto, K., Mamori, H. & Murata, A. 2019 Pathline analysis of traveling wavy blowing and suction control in turbulent pipe flow for drag reduction. Intl J. Heat Fluid Flow 77, 388–401.CrossRefGoogle Scholar
Lee, C., Min, T. & Kim, J. 2008 Stability of channel flow subject to wall blowing and suction in the form of travelling waves. Phys. Fluids 20, 101513.CrossRefGoogle Scholar
Lieu, B.K., Moarref, R. & Jovanovič, M. 2010 Controlling the onset of turbulence by streamwise travelling waves. Part 2. Direct numerical simulations. J. Fluid Mech. 663, 100–119.CrossRefGoogle Scholar
Mamori, H., Iwamoto, K. & Marata, A. 2014 Effect of the parameters of travelling waves created by blowing and suction on the relaminarization phenomena in fully developed turbulent channel flow. Phys. Fluids 26, 015101.CrossRefGoogle Scholar
Marusic, I., Joseph, D.D. & Nahesh, K. 2007 Laminar and turbulent comparisons for channel flow and flow control. J. Fluid Mech. 570, 467–477.CrossRefGoogle Scholar
Min, T., Kang, S.M., Speyer, J.L. & Kim, J. 2006 Sustained sub-laminar drag in a fully developed channel flow. J. Fluid Mech. 558, 309–318.CrossRefGoogle Scholar
Moarref, R. & Jovanovič, M. 2010 Controlling the onset of turbulence by streamwise travelling waves. Part 1. Receptivity analysis. J. Fluid Mech. 663, 70–99.CrossRefGoogle Scholar
Mohammadi, A. & Floryan, J.M. 2012 Mechanism of drag generation by surface corrugation. Phys. Fluids 24, 013602.CrossRefGoogle Scholar
Mohammadi, A. & Floryan, J.M. 2013 a Pressure losses in grooved channel. J. Fluid Mech. 725, 23–54.CrossRefGoogle Scholar
Mohammadi, A. & Floryan, J.M. 2013 b Groove optimization for drag reduction. Phys. Fluids 25, 113601.CrossRefGoogle Scholar
Mohammadi, A. & Floryan, J.M. 2014 Effects of longitudinal grooves on the Couette-Poiseuille flow. J. Theor. Comput. Fluid Dyn. 28, 549–572.CrossRefGoogle Scholar
Mohammadi, A. & Floryan, J.M. 2015 Numerical analysis of laminar-drag-reducing grooves. J. Fluids Engng 137, 041201.CrossRefGoogle Scholar
Mohammadi, A., Moradi, H.V. & Floryan, J.M. 2015 New instability mode in a grooved channel. J. Fluid Mech. 778, 691–720.CrossRefGoogle Scholar
Moradi, H.V. & Floryan, J.M. 2013 Flows in annuli with longitudinal grooves. J. Fluid Mech. 716, 280–315.CrossRefGoogle Scholar
Moradi, H.V. & Floryan, J.M. 2014 Stability of flow in a channel with longitudinal grooves. J. Fluid Mech. 757, 613–648.CrossRefGoogle Scholar
Ou, J., Perot, J.B. & Rothstein, J.P. 2004 Laminar drag reduction in microchannels using ultrahydrophobic surfaces. Phys. Fluids 16, 4635.CrossRefGoogle Scholar
Ou, J. & Rothstein, J.P. 2005 Direct velocity measurements of the flow past drag-reducing ultrahydrophobic surfaces. Phys. Fluids 17, 103606.CrossRefGoogle Scholar
Park, H., Park, H. & Kim, J. 2013 A numerical study of the effects of superhydrophobic surface on skin-friction drag in turbulent channel flow. Phys. Fluids 25, 110815.CrossRefGoogle Scholar
Park, H., Sun, G. & Kim, J. 2014 Superhydrophobic turbulent drag reduction as a function of surface grating parameters. J. Fluid Mech. 747, 722–734.CrossRefGoogle Scholar
Perot, J.B. & Rothstein, J.P. 2004 Laminar drag reduction in microchannels using ultrahydrophobic surfaces. Phys. Fluids 16, 4635–4643.Google Scholar
Poetes, R., Holtzmann, K., Franze, K. & Steiner, U. 2010 Metastable underwater superhydrophobicity. Phys. Rev. Lett. 105, 166104.CrossRefGoogle ScholarPubMed
Quadrio, M., Floryan, J.M. & Luchini, P. 2005 Modification of turbulent flow using distributed suction. CASI J. 51, 61–69.Google Scholar
Quadrio, M., Floryan, J.M. & Luchini, P. 2007 Effects of streamwise-periodic wall transpiration on turbulent friction drag. J. Fluid Mech. 507, 425–444.CrossRefGoogle Scholar
Raayai-Ardakani, S. & McKinley, G.H. 2017 Drag reduction using wrinkled surfaces in high Reynolds number laminar boundary layer flows. Phys. Fluids 29, 093605.CrossRefGoogle Scholar
Roberts, P.J.D. & Floryan, J.M. 2002 Instability of accelerated boundary layers induced by surface suction. AIAA J. 40, 851–859.CrossRefGoogle Scholar
Roberts, P.J.D. & Floryan, J.M. 2008 Instability of adverse-pressure-gradient boundary layers with suction. AIAA J. 46, 2416–2423.CrossRefGoogle Scholar
Roberts, P.J.D., Floryan, J.M., Casalis, G. & Arnal, D. 2001 Boundary layers instability induced by wall suction. Phys. Fluids 13, 2543–2553.CrossRefGoogle Scholar
Rosenberg, B.J., Van Buren, T., Fu, M.K. & Smits, A.J. 2016 Turbulent drag reduction over air- and liquid-impregnated surfaces. Phys. Fluids 28, 015103.CrossRefGoogle Scholar
Rothstein, J.P. 2010 Slip on superhydrophobic surfaces. Ann. Rev. Fluid Mech. 42, 89–109.CrossRefGoogle Scholar
Samaha, M.A., Tafreshi, H.V. & Gad-el-Hak, M. 2011 Modeling drag reduction and meniscus stability of superhydrophobic surfaces comprised of random roughness. Phys. Fluids 23, 012001.CrossRefGoogle Scholar
Solomon, B.R., Khalil, K.S. & Varanasi, K.K. 2014 Drag reduction using lubricant impregnated surfaces in viscous laminar flow. Langmuir 30, 10970–10976.CrossRefGoogle ScholarPubMed
Solomon, B.R., Khalil, K.S. & Varanasi, K.K. 2016 Drag reduction using lubricant-impregnated surfaces in viscous flows. Langmuir 32, 8287–8287.CrossRefGoogle Scholar
Srinivasan, S., Choi, W., Park, K.C.L., Chatre, S.S., Cohen, R.E. & Mckinley, G.H. 2013 Drag reduction for viscous laminar flow on spray-coated non-wetting surfaces. Soft Matt. 9, 5691–5702.CrossRefGoogle Scholar
Sumitani, Y. & Kasagi, N. 1995 Direct numerical simulation of turbulent transport with uniform wall injection and suction. AIAA J. 33, 1220–1228.CrossRefGoogle Scholar
Szumbarski, J. 2007 Instability of viscous incompressible flow in a channel with transversely corrugated walls. J. Theor. Appl. Mech. 45, 659–683.Google Scholar
Szumbarski, J., Blonski, S. & Kowalewski, T.A. 2011 Impact of transversely-oriented wall corrugation on hydraulic resistance of a channel flow. Arch. Mech. Engng 58, 441–466.Google Scholar
Szumbarski, J. & Floryan, J.M. 2000 Tollmien-schlichting instability of channel flow in the presence of weak distributed suction. AIAA J. 38, 372–374.CrossRefGoogle Scholar
Tilton, N. & Cortelezzi, L. 2008 Linear stability analysis of pressure-driven flows in channels with porous walls. J. Fluid Mech. 604, 411–445.CrossRefGoogle Scholar
Van Buren, T. & Smits, A.J. 2017 Substantial drag reduction in turbulent flow using liquid-infused surfaces. J. Fluid Mech. 827, 448–456.CrossRefGoogle Scholar
Walsh, M.J. 1980 Drag characteristics of V-groove and transverse curvature riblets. In Viscous Drag Reduction (ed. G.R. Hough), vol. 72, pp. 168–184. AIAA.CrossRefGoogle Scholar
Walsh, M.J. 1983 Riblets as a viscous drag reduction technique. AIAA J. 21, 485–486.CrossRefGoogle Scholar
Waltz, R.A., Morales, J.L., Nocedal, J. & Orban, D. 2006 An interior algorithm for nonlinear optimization that combines line search and trust region steps. Math. Program. Ser. A 107, 391–408.CrossRefGoogle Scholar
Wong, T.S., Kang, S.H., Tang, S.K.Y., Smythe, E.J., Hatton, B.D., Grinthal, A. & Aizenberg, J. 2011 Bioinspired self-repairing slippery surfaces with pressure-stable omniphobicity. Nature 477, 443–447.CrossRefGoogle ScholarPubMed
Woodcock, J.D., Sader, J.E. & Marusic, I. 2012 Induced flow due to blowing and suction flow control: an analysis of transpiration. J. Fluid Mech. 690, 366–398.CrossRefGoogle Scholar
Yadav, N., Gepner, S.W. & Szumbarski, J. 2017 Instability in a channel with grooves parallel to the flow. Phys. Fluids 29, 084104.CrossRefGoogle Scholar
Yadav, N., Gepner, S.W. & Szumbarski, J. 2018 Flow dynamics in longitudinally grooved duct. Phys. Fluids 30, 104105.CrossRefGoogle Scholar