Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-01-09T21:47:54.240Z Has data issue: false hasContentIssue false
  • English
  • Français

On the universality of turbulent axisymmetric wakes

Published online by Cambridge University Press:  05 September 2012

John A. Redford ,
Ian P. Castro  and
Gary N. Coleman
John A. Redford
Affiliation:
Aerodynamics and Flight Mechanics Research Group, University of Southampton, Highfield, Southampton SO17 1BJ, UK
Ian P. Castro
Affiliation:
Aerodynamics and Flight Mechanics Research Group, University of Southampton, Highfield, Southampton SO17 1BJ, UK
Gary N. Coleman*
Affiliation:
Aerodynamics and Flight Mechanics Research Group, University of Southampton, Highfield, Southampton SO17 1BJ, UK
*
†Present address: Computational Aerosciences Branch, NASA Langley Research Center, Hampton, VA 23681, USA. Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Direct numerical simulations (DNS) of two time-dependent, axially homogeneous, axisymmetric turbulent wakes having very different initial conditions are presented in order to assess whether they reach a universal self-similar state as classically hypothesized by Townsend. It is shown that an extensive early-time period exists during which the two wakes are individually self-similar with wake widths growing like 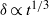, as predicted by classical dimensional analysis, but have very different growth rates and are thus not universal. Subsequently, however, the turbulence adjusts to yield, eventually, wakes that are structurally identical and have the same growth rate (also with 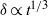) so provide clear evidence of a universal, self-similar state. The former non-universal but self-similar state extends, in terms of a spatially equivalent flow behind a spherical body of diameter 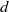, to a distance of 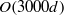whereas the final universal state does not appear before 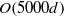(and exists despite relatively low values of the Reynolds number and no evidence of a spectral 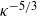inertial subrange). Universal wake evolution is therefore likely to be rare in practice. Despite its low Reynolds number, the flow does not exhibit the sometime-suggested alternative self-similar behaviour with 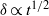(as for the genuinely laminar case) at large times (or, equivalently, distances), since the eddy viscosity remains large compared to the molecular viscosity and its temporal variations are not negligible.

JFM classification

Turbulent Flows: Shear layer turbulence Turbulent Flows: Turbulence simulation Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 710 , 10 November 2012 , pp. 419 - 452
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Archer, P. J., Thomas, T. G. & Coleman, G. N. 2008 Direct numerical simulations of vortex ring evolution from laminar to the early turbulent regime. J. Fluid Mech. 598, 201–206.CrossRefGoogle Scholar
2. Basu, A. J., Narasimha, R. & Sinha, U. N. 1992 Direct numerical simulation of the initial evolution of a turbulent axisymmetric wake. Curr. Sci. 63, 734–740.Google Scholar
3. Bevilaqua, P. M. & Lykoudis, P. S. 1978 Turbulence memory in self-preserving wakes. J. Fluid Mech. 89 (3), 589–606.CrossRefGoogle Scholar
4. Cannon, S. F. & Champagne, F. 1991 Large-scale structures in wakes behind axisymmetric bodies. In Proceedings Eighth Symposium on Turbulent Shear Flows, Munich, pp. 6.5.1–6.5.6.Google Scholar
5. Chevray, R. 1968 The turbulent wake of a body of revolution. Trans. ASME: J. Basic Engng 90, 275–284.CrossRefGoogle Scholar
6. Dommermuth, D. G., Rottman, J. W., Innis, G. E. & Novikov, E. A. 2002 Numerical simulation of the wake of a towed sphere in a weakly stratified fluid. J. Fluid Mech. 473, 83–101.CrossRefGoogle Scholar
7. Ewing, D., George, W. K., Rogers, M. M. & Moser, R. D. 2007 Two-point similarity in temporally evolving plane wakes. J. Fluid Mech. 577, 287–307.CrossRefGoogle Scholar
8. George, W. K. 1989 The self-preservation of turbulent flows and its relation to initial conditions and coherent structure. In Advances in Turbulence (ed. George, W. K. & Arndt, R. ), pp. 39–73. Hemisphere.Google Scholar
9. George, W. K. 2008 Freeman Lecture: Is there an asymptotic effect on initial and upstream conditions on turbulence? FEDSM2008-55362. In Proceedings of ASME 2008 Fluids Engineering Meeting, pp. 1–26. ASME.Google Scholar
10. George, W. K. & Davidson, L. 2004 Role of initial conditions in establishing asymptotic flow behaviour. AIAA J. 42 (3), 438–446.CrossRefGoogle Scholar
11. Gottlieb, D. & Orszag, S. A. 1977 Numerical Analysis of Spectral Methods: Theory and Applications. SIAM.CrossRefGoogle Scholar
12. Gourlay, M. J., Arendt, S. C., Fritts, D. C. & Werne, J. 2001 Numerical modelling of initially turbulent wakes with net momentum. Phys. Fluids 13 (12), 3783–3802.CrossRefGoogle Scholar
13. Jiménez, J. & Moin, P. 1991 The minimal flow unit in near-wall turbulence. J. Fluid Mech. 225, 213–240.CrossRefGoogle Scholar
14. Johansson, P. B. V., George, W. K. & Gourlay, M. J. 2003 Equilibrium similarity, effects of initial conditions and local Reynolds number on the axisymmetric wake. Phys. Fluids 15 (3), 603–617.CrossRefGoogle Scholar
15. Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.CrossRefGoogle Scholar
16. Moser, R. D., Rogers, M. M. & Ewing, D. W. 1998 Self-similarity of time-evolving plane wakes. J. Fluid Mech. 367, 255–289.CrossRefGoogle Scholar
17. Narasimha, R. 1992 The utility and drawbacks of traditional approaches. In Whither Turbulence? (ed. Lumley, J. ). pp. 13–49. Springer.Google Scholar
18. Narasimha, R. & Prabhu, A. 1972 Equilibrium and relaxation in turbulent wakes. J. Fluid Mech. 54, 1–17.CrossRefGoogle Scholar
19. Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
20. Rogallo, R. S. 1981 Numerical experiments in homogeneous turbulence. NASA Technical Memorandum 81315.Google Scholar
21. Sandham, N. D. 2002 Introduction to direct numerical simulation. In Closure Strategies for Turbulent and Transitional Flows (ed. Launder, B. E. & Sandham, N. D. ). pp. 248–266. Cambridge University Press.CrossRefGoogle Scholar
22. Shariff, K., Verzicco, R. & Orlandi, P. 1994 Three-dimensional vortex ring instabilities. J. Fluid Mech. 279, 351–375.CrossRefGoogle Scholar
23. Spalart, P. E., Moser, R. D. & Rogers, M. M. 1991 Spectral methods for the Navier–Stokes equations with one infinite and two periodic directions. J. Comput. Phys. 96 (2), 297–324.CrossRefGoogle Scholar
24. Sreenivasan, K. R. 1981 Approach to self-preservation in plane turbulent wakes. AIAA J. 19, 1365–1367.CrossRefGoogle Scholar
25. Sreenivasan, K. R. & Narasimha, R. 1982 Equilibrium parameters for two-dimensional turbulent wakes. Trans. ASME: J. Fluids Engng 104, 167–170.Google Scholar
26. Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT.CrossRefGoogle Scholar
27. Townsend, A. A. 1956 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
28. Townsend, A. A. 1976 Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
29. Zhou, Y. & Antonia, R. A. 1995 Memory effects in a turbulent plane wake. Exp. Fluids 19, 112–120.CrossRefGoogle Scholar