Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-29T08:02:53.203Z Has data issue: false hasContentIssue false
  • English
  • Français

On the turbulence modelling of waves breaking on a vertical pile

Published online by Cambridge University Press:  02 December 2022

Yuzhu Li Open the ORCID record for Yuzhu Li [Opens in a new window]  and
David R. Fuhrman Open the ORCID record for David R. Fuhrman [Opens in a new window]
Yuzhu Li*
Affiliation:
Department of Civil and Environmental Engineering, National University of Singapore, 117576, Republic of Singapore Department of Mechanical Engineering, Section for Fluid Mechanics, Coastal and Maritime Engineering, Technical University of Denmark, 2800 Kgs. Lyngby, Denmark
David R. Fuhrman
Affiliation:
Department of Mechanical Engineering, Section for Fluid Mechanics, Coastal and Maritime Engineering, Technical University of Denmark, 2800 Kgs. Lyngby, Denmark
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

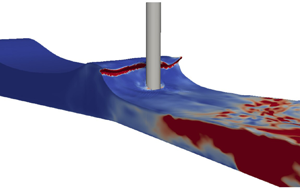
Incipient wave breaking on a vertical circular pile is simulated with a Reynolds stress–$\omega$ turbulence model. Comparison of results simulated with a stabilized two-equation turbulence model, as well as no turbulence model, demonstrates that the breaking point and the peak force on a vertical cylinder due to incipient breaking should not be affected by the turbulence closure model, provided that it is stable and the simulations are converged. Notably, the present results show that the build-up to peak force induced by incipient wave breaking can be accurately predicted without any turbulence closure model. However, for the prediction of the secondary load cycle (SLC), proper turbulence modelling is required, as this process involves both turbulence production and lee-side flow separation. The Reynolds stress–$\omega$ model is demonstrated to predict the SLC more accurately than a stabilized two-equation $k$–$\omega$ turbulence model, as the flow separation points and vorticity field are better predicted. Some existing studies indicate that the generation of the SLC does not necessarily result from flow separation, but is rather due to the suction force. The present work finds that the occurrence and point of flow separation significantly affect the magnitude of the suction force, which hence affects the SLC prediction significantly. For waves breaking on a vertical pile, proper turbulence modelling is therefore essential for accurate SLC predictions. (In the above, $k$ is the turbulent kinetic energy density and $\omega$ is the specific dissipation rate.)

JFM classification

Turbulent Flows: Turbulence modelling Waves/Free-surface Flows: Wave breaking
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 953 , 25 December 2022 , A3
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Antolloni, G., Jensen, A., Grue, J., Riise, B.H. & Brocchini, M. 2020 Wave-induced vortex generation around a slender vertical cylinder. Phys. Fluids 32 (4), 042105.CrossRefGoogle Scholar
Apelt, C.J. & Piorewicz, J. 1987 Laboratory studies of breaking wave forces acting on vertical cylinders in shallow water. Coast. Engng 11 (3), 263–282.CrossRefGoogle Scholar
Bihs, H., Kamath, A., Chella, M.A. & Arntsen, Ø.A. 2016 Breaking-wave interaction with tandem cylinders under different impact scenarios. ASCE J. Waterway Port Coastal Ocean Engng 142 (5), 04016005.CrossRefGoogle Scholar
Brown, S.A., Greaves, D.M., Magar, V. & Conley, D.C. 2016 Evaluation of turbulence closure models under spilling and plunging breakers in the surf zone. Coast. Engng 114, 177–193.CrossRefGoogle Scholar
Chaplin, J.R., Rainey, R.C.T. & Yemm, R.W. 1997 Ringing of a vertical cylinder in waves. J. Fluid Mech. 350, 119–147.CrossRefGoogle Scholar
Choi, S.-J., Lee, K.-H. & Gudmestad, O.T. 2015 The effect of dynamic amplification due to a structure's vibration on breaking wave impact. Ocean Engng 96, 8–20.CrossRefGoogle Scholar
Derakhti, M., Kirby, J.T., Shi, F. & Ma, G. 2016 Wave breaking in the surf zone and deep-water in a non-hydrostatic RANS model. Part 1: organized wave motions. Ocean Model. 107, 125–138.CrossRefGoogle Scholar
Devolder, B., Troch, P. & Rauwoens, P. 2018 Performance of a buoyancy-modified $k$-$\omega$ and $k$-$\omega$ SST turbulence model for simulating wave breaking under regular waves using OpenFOAM$^{\circledR}$. Coast. Engng 138, 49–65.CrossRefGoogle Scholar
Dubief, Y. & Delcayre, F. 2000 On coherent-vortex identification in turbulence. J. Turbul. 1 (1), 011.CrossRefGoogle Scholar
Fenton, J.D. 1988 The numerical solution of steady water wave problems. Comput. Geosci. 14 (3), 357–368.CrossRefGoogle Scholar
Fuhrman, D.R. & Larsen, B.E. 2020 A discussion on “numerical computations of resonant sloshing using the modified isoadvector method and the buoyancy-modified turbulence closure model” [Appl. Ocean Res. (2019), 93, article no. 101829, doi:10.1016.j.apor.2019.05.014]. Appl. Ocean Res. 99, 102159.CrossRefGoogle Scholar
Fuhrman, D.R. & Li, Y. 2020 Instability of the realizable $k$-$\varepsilon$ turbulence model beneath surface waves. Phys. Fluids 32, 115108.CrossRefGoogle Scholar
Ghadirian, A. & Bredmose, H. 2020 Detailed force modelling of the secondary load cycle. J. Fluid Mech. 889, A21.CrossRefGoogle Scholar
Grue, J., Bjørshol, G. & Strand, Ø. 1993 Higher harmonic wave exciting forces on a vertical cylinder. In Applied Mathematics, vol. September, pp. 1–30. Matematisk Institutt, Universitetet i Oslo.Google Scholar
Grue, J. & Huseby, M. 2002 Higher-harmonic wave forces and ringing of vertical cylinders. Appl. Ocean Res. 24 (4), 203–214.CrossRefGoogle Scholar
Hall, M.A. 1958 Laboratory Study of Breaking Wave Forces on Piles. Technical Memorandum, vol. 106. Beach Erosion Board.Google Scholar
Honda, T. & Mitsuyasu, H. 1974 Experimental study of breaking wave force on a vertical circular cylinder. Coast. Engng J. 17 (1), 59–70.CrossRefGoogle Scholar
Hsu, T.J., Sakakiyama, T. & Liu, P.L.-F. 2002 A numerical model for wave motions and turbulence flows in front of a composite breakwater. Coast. Engng 46 (1), 25–50.CrossRefGoogle Scholar
Irschik, K., Sparboom, U. & Oumeraci, H. 2004 Breaking wave loads on a slender pile in shallow water. In 29th International Conference of Coast. Eng. (ed. J. McKee Smith), pp. 568–580. World Scientific.Google Scholar
Jacobsen, N.G., Fuhrman, D.R. & Fredsøe, J. 2012 A wave generation toolbox for the open-source CFD library: OpenFOAM$^{\circledR}$. Intl J. Numer. Meth. Fluids 70 (9), 1073–1088.CrossRefGoogle Scholar
Jang, H.K., Ozdemir, C.E., Liang, J.-H. & Tyagi, M. 2021 Oscillatory flow around a vertical wall-mounted cylinder: flow pattern details. Phys. Fluids 33 (2), 025114.CrossRefGoogle Scholar
Jose, J., Choi, S.-J., Giljarhus, K.E.T. & Gudmestad, O.T. 2017 A comparison of numerical simulations of breaking wave forces on a monopile structure using two different numerical models based on finite difference and finite volume methods. Ocean Engng 137, 78–88.CrossRefGoogle Scholar
Kamath, A., Chella, M.A., Bihs, H. & Arntsen, Ø.A. 2016 Breaking wave interaction with a vertical cylinder and the effect of breaker location. Ocean Engng 128, 105–115.CrossRefGoogle Scholar
Kristiansen, T. & Faltinsen, O.M. 2017 Higher harmonic wave loads on a vertical cylinder in finite water depth. J. Fluid Mech. 833, 773–805.CrossRefGoogle Scholar
Kyte, A. & Tørum, A. 1996 Wave forces on vertical cylinders upon shoals. Coast. Engng 27 (3–4), 263–286.CrossRefGoogle Scholar
Larsen, B.E. & Fuhrman, D.R. 2018 On the over-production of turbulence beneath surface waves in Reynolds-averaged Navier–Stokes models. J. Fluid Mech. 853, 419–460.CrossRefGoogle Scholar
Larsen, B.E., Fuhrman, D.R. & Roenby, J. 2019 Performance of interFoam on the simulation of progressive waves. Coast. Engng J. 61 (3), 380–400.CrossRefGoogle Scholar
Launder, B.E., Reece, G.J. & Rodi, W. 1975 Progress in the development of a Reynolds-stress turbulence closure. J. Fluid Mech. 68 (3), 537–566.CrossRefGoogle Scholar
Li, Y. & Fuhrman, D.R. 2021 Computational fluid dynamics simulation of deep-water wave instabilities involving wave breaking. J. Offshore Mech. Arctic Engng 144 (2), 021901.CrossRefGoogle Scholar
Li, Y., Larsen, B.E. & Fuhrman, D.R. 2022 Reynolds stress turbulence modelling of surf zone breaking waves. J. Fluid Mech. 937, A7.CrossRefGoogle Scholar
Li, Y., Ong, M.C., Fuhrman, D.R. & Larsen, B.E. 2020 Numerical investigation of wave-plus-current induced scour beneath two submarine pipelines in tandem. Coast. Engng 156, 103619.CrossRefGoogle Scholar
Lin, P. & Liu, P.L.-F. 1998 A numerical study of breaking waves in the surf zone. J. Fluid Mech. 359, 239–264.CrossRefGoogle Scholar
Liu, S., Jose, J., Ong, M.C. & Gudmestad, O.T. 2019 Characteristics of higher-harmonic breaking wave forces and secondary load cycles on a single vertical circular cylinder at different Froude numbers. Mar. Struct. 64, 54–77.CrossRefGoogle Scholar
Menter, F.R. 1994 Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 32 (8), 1598–1605.CrossRefGoogle Scholar
Morison, J.R., Johnson, J.W. & Schaaf, S.A. 1950 The force exerted by surface waves on piles. J. Petrol. Tech. 2 (05), 149–154.CrossRefGoogle Scholar
Naot, D. & Rodi, W. 1982 Calculation of secondary currents in channel flow. ASCE J. Hydraul. Engng 108 (8), 948–968.Google Scholar
Paulsen, B.T., Bredmose, H., Bingham, H.B. & Jacobsen, N.G. 2014 Forcing of a bottom-mounted circular cylinder by steep regular water waves at finite depth. J. Fluid Mech. 755, 1–34.CrossRefGoogle Scholar
Qu, S., Liu, S. & Ong, M.C. 2021 An evaluation of different RANS turbulence models for simulating breaking waves past a vertical cylinder. Ocean Engng 234, 109195.CrossRefGoogle Scholar
Shih, T.-H., Liou, W.W., Shabbir, A., Yang, Z. & Zhu, J. 1995 A new $k$-$\varepsilon$ eddy viscosity model for high Reynolds number turbulent flows. Comput. Fluids 24 (3), 227–238.CrossRefGoogle Scholar
Smagorinsky, J. 1963 General circulation experiments with the primitive equations: I. The basic experiment. Mon. Weath. Rev. 91 (3), 99–164.2.3.CO;2>CrossRefGoogle Scholar
Sumer, B.M. & Fuhrman, D.R. 2020 Turbulence in Coastal and Civil Engineering. World Scientific.CrossRefGoogle Scholar
Wiegel, R.L. 1982 Forces induced by breakers on piles. In 18th International Conference on Coast. Eng. (ed. B. L. Edge), pp. 1699–1715. American Society of Civil Engineers.CrossRefGoogle Scholar
Wienke, J. & Oumeraci, H. 2005 Breaking wave impact force on a vertical and inclined slender pile-theoretical and large-scale model investigations. Coast. Engng 52 (5), 435–462.CrossRefGoogle Scholar
Wilcox, D.C. 2006 Turbulence Modeling for CFD, 3rd edn. DCW Industries.Google Scholar
Wilcox, D.C. 2008 Formulation of the $k$-$\omega$ turbulence model revisited. AIAA J. 46 (11), 2823–2838.CrossRefGoogle Scholar
Xu, F. & Wang, Y. 2021 Numerical simulation of ringing responses of a vertical cylinder. Ocean Engng 226, 108815.CrossRefGoogle Scholar