Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Fedele, F.
Chandre, C.
and
Farazmand, M.
2016.
Kinematics of fluid particles on the sea surface: Hamiltonian theory.
Journal of Fluid Mechanics,
Vol. 801,
Issue. ,
p.
260.
Eeltink, D.
Lemoine, A.
Branger, H.
Kimmoun, O.
Kharif, C.
Carter, J. D.
Chabchoub, A.
Brunetti, M.
and
Kasparian, J.
2017.
Spectral up- and downshifting of Akhmediev breathers under wind forcing.
Physics of Fluids,
Vol. 29,
Issue. 10,
Longo, Sandro
Clavero, Maria
Chiapponi, Luca
and
Losada, Miguel
2017.
Invariants of Turbulence Reynolds Stress and of Dissipation Tensors in Regular Breaking Waves.
Water,
Vol. 9,
Issue. 11,
p.
893.
Fedele, Francesco
Lugni, Claudio
and
Chawla, Arun
2017.
The sinking of the El Faro: predicting real world rogue waves during Hurricane Joaquin.
Scientific Reports,
Vol. 7,
Issue. 1,
Seiffert, Betsy R.
Ducrozet, Guillaume
and
Bonnefoy, Félicien
2017.
Simulation of breaking waves using the high-order spectral method with laboratory experiments: Wave-breaking onset.
Ocean Modelling,
Vol. 119,
Issue. ,
p.
94.
Barthelemy, X.
Banner, M. L.
Peirson, W. L.
Fedele, F.
Allis, M.
and
Dias, F.
2018.
On a unified breaking onset threshold for gravity waves in deep and intermediate depth water.
Journal of Fluid Mechanics,
Vol. 841,
Issue. ,
p.
463.
Hasan, S.A.
Sriram, V.
and
Panneer Selvam, R.
2018.
Numerical modelling of wind-modified focused waves in a numerical wave tank.
Ocean Engineering,
Vol. 160,
Issue. ,
p.
276.
Seiffert, Betsy R.
and
Ducrozet, Guillaume
2018.
Simulation of breaking waves using the high-order spectral method with laboratory experiments: wave-breaking energy dissipation.
Ocean Dynamics,
Vol. 68,
Issue. 1,
p.
65.
Saket, Arvin
Peirson, William L.
Banner, Michael L.
and
Allis, Michael J.
2018.
On the influence of wave breaking on the height limits of two-dimensional wave groups propagating in uniform intermediate depth water.
Coastal Engineering,
Vol. 133,
Issue. ,
p.
159.
Derakhti, Morteza
Banner, Michael L.
and
Kirby, James T.
2018.
Predicting the breaking strength of gravity water waves in deep and intermediate depth.
Journal of Fluid Mechanics,
Vol. 848,
Issue. ,
Khait, A.
and
Shemer, L.
2018.
On the kinematic criterion for the inception of breaking in surface gravity waves: Fully nonlinear numerical simulations and experimental verification.
Physics of Fluids,
Vol. 30,
Issue. 5,
McAllister, M. L.
Draycott, S.
Adcock, T. A. A.
Taylor, P. H.
and
van den Bremer, T. S.
2019.
Laboratory recreation of the Draupner wave and the role of breaking in crossing seas.
Journal of Fluid Mechanics,
Vol. 860,
Issue. ,
p.
767.
Simon, Bruno
Papoutsellis, Christos E.
Benoit, Michel
and
Yates, Marissa L.
2019.
Comparing methods of modeling depth-induced breaking of irregular waves with a fully nonlinear potential flow approach.
Journal of Ocean Engineering and Marine Energy,
Vol. 5,
Issue. 4,
p.
365.
Dong, Guohai
Fu, Ruili
Ma, Yuxiang
and
Fang, Kezhao
2019.
Simulation of unidirectional propagating wave trains in deep water using a fully non-hydrostatic model.
Ocean Engineering,
Vol. 180,
Issue. ,
p.
254.
Hasan, S.A.
Sriram, V.
and
Selvam, R. Panneer
2019.
Evaluation of an eddy viscosity type wave breaking model for intermediate water depths.
European Journal of Mechanics - B/Fluids,
Vol. 78,
Issue. ,
p.
115.
Craciunescu, C C
and
Christou, M
2019.
The effect of wave crest speed in breaking waves.
IOP Conference Series: Materials Science and Engineering,
Vol. 586,
Issue. 1,
p.
012039.
Herterich, James G.
and
Dias, Frédéric
2019.
Extreme long waves over a varying bathymetry.
Journal of Fluid Mechanics,
Vol. 878,
Issue. ,
p.
481.
Fedele, Francesco
Herterich, James
Tayfun, Aziz
and
Dias, Frederic
2019.
Large nearshore storm waves off the Irish coast.
Scientific Reports,
Vol. 9,
Issue. 1,
Pizzo, Nick
and
Kendall Melville, W.
2019.
Focusing deep-water surface gravity wave packets: wave breaking criterion in a simplified model.
Journal of Fluid Mechanics,
Vol. 873,
Issue. ,
p.
238.
Ardag, Dorukhan
and
Resio, Donald T.
2020.
A New Approach for Modeling Dissipation due to Breaking in Wind Wave Spectra.
Journal of Physical Oceanography,
Vol. 50,
Issue. 2,
p.
439.
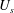 $U_{s}$) with the wave crest point speed (
$U_{s}$) with the wave crest point speed (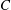 $C$) determined by an array of closely spaced wave gauges. The crest point surface energy flux ratio
$C$) determined by an array of closely spaced wave gauges. The crest point surface energy flux ratio 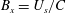 $B_{x}=U_{s}/C$ that distinguishes maximum recurrence from marginal breaking was found to be
$B_{x}=U_{s}/C$ that distinguishes maximum recurrence from marginal breaking was found to be 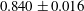 $0.840\pm 0.016$. Increasing wind forcing from zero to
$0.840\pm 0.016$. Increasing wind forcing from zero to 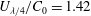 $U_{\unicode[STIX]{x1D706}/4}/C_{0}=1.42$ systematically increased this threshold by 2 %. Increasing the spectral bandwidth (decreasing the Benjamin–Feir index from 0.39 to 0.31) systematically reduced the threshold by 1.5 %.
$U_{\unicode[STIX]{x1D706}/4}/C_{0}=1.42$ systematically increased this threshold by 2 %. Increasing the spectral bandwidth (decreasing the Benjamin–Feir index from 0.39 to 0.31) systematically reduced the threshold by 1.5 %.