Published online by Cambridge University Press: 05 December 2011
In the context of an Eulerian fluid description, we investigate the dynamics of a shock wave that is driven by the steady impulsively initiated motion of a two-dimensional planar piston with small corrugations superimposed on its surface. This problem was originally solved by Freeman (Proc. Royal Soc. A, vol. 228, 1955, pp. 341–362), who showed that piston-driven shocks are unconditionally stable when the fluid medium through which they propagate is an ideal gas. Here, we generalize Freeman’s mathematical framework to account for a fluid characterized by an arbitrary equation of state. We find that a sufficient condition for shock stability is  , where
, where 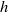 is the D’yakov parameter and
is the D’yakov parameter and 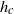 is a critical value less than unity. For values of
is a critical value less than unity. For values of 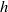 within this range, linear perturbations imparted to the front by the piston at time
within this range, linear perturbations imparted to the front by the piston at time 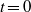 attenuate asymptotically as
attenuate asymptotically as 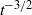 . Outside of this range, the temporal behaviour of perturbations is more difficult to determine and further analysis is required to assess the stability of a shock front under such circumstances. As a benchmark of the main conclusions of this paper, we compare our generalized expression for the linearized shock-ripple amplitude with an independent Bessel-series solution derived by Zaidel’ (J. Appl. Math. Mech., vol. 24, 1960, pp. 316–327) and find excellent agreement.
. Outside of this range, the temporal behaviour of perturbations is more difficult to determine and further analysis is required to assess the stability of a shock front under such circumstances. As a benchmark of the main conclusions of this paper, we compare our generalized expression for the linearized shock-ripple amplitude with an independent Bessel-series solution derived by Zaidel’ (J. Appl. Math. Mech., vol. 24, 1960, pp. 316–327) and find excellent agreement.