Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-22T19:16:43.758Z Has data issue: false hasContentIssue false
  • English
  • Français

On the structure of steady parasitic gravity-capillary waves in the small surface tension limit

Published online by Cambridge University Press:  09 July 2021

Josh Shelton Open the ORCID record for Josh Shelton [Opens in a new window] ,
Paul Milewski Open the ORCID record for Paul Milewski [Opens in a new window]  and
Philippe H. Trinh Open the ORCID record for Philippe H. Trinh [Opens in a new window]
Josh Shelton*
Affiliation:
Department of Mathematical Sciences, University of Bath, BathBA2 7AY, UK
Paul Milewski
Affiliation:
Department of Mathematical Sciences, University of Bath, BathBA2 7AY, UK
Philippe H. Trinh*
Affiliation:
Department of Mathematical Sciences, University of Bath, BathBA2 7AY, UK
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

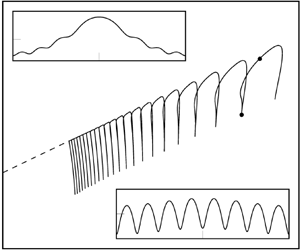
When surface tension is included in the classical formulation of a steadily travelling gravity wave (a Stokes wave), it is possible to obtain solutions that exhibit parasitic ripples: small capillary waves riding on the surface of steep gravity waves. However, it is not clear whether the singular small surface tension limit is well posed. That is, is it possible for an appropriate travelling gravity-capillary wave to be continuously deformed to the classic Stokes wave in the limit of vanishing surface tension? The work of Chen & Saffman (Stud. Appl. Maths, vol. 62, issue 1, 1980, pp. 1–21) had suggested smooth continuation was not possible, while the numerical study of Schwartz & Vanden-Broeck (J. Fluid Mech., vol. 95, issue 1, 1979, pp. 119–139) used an amplitude parameter that made it difficult to understand the structure of solutions for small values of the surface tension. In this paper we numerically explore the low surface tension limit of the steep gravity-capillary travelling-wave problem. Our results allow for a classification of the bifurcation structure that arises, and serve to unify a number of previous numerical studies. Crucially, we demonstrate that different choices of solution amplitude can lead to subtle restrictions on the continuation procedure. When wave energy is used as a continuation parameter, solution branches can be continuously deformed to the zero surface tension limit of a travelling Stokes wave.

JFM classification

Waves/Free-surface Flows: Capillary waves Waves/Free-surface Flows: Surface gravity waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 922 , 10 September 2021 , A16
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Binder, B.J., Dias, F. & Vanden-Broeck, J.-M. 2008 Influence of rapid changes in a channel bottom on free-surface flows. IMA J. Appl. Maths 73 (1), 254–273.CrossRefGoogle Scholar
Boyd, J.P. 1998 Weakly Nonlocal Solitary Waves and Beyond-All-Orders Asymptotics. Kluwer Academic.CrossRefGoogle Scholar
Chapman, S.J., King, J.R. & Adams, K.L. 1998 Exponential asymptotics and Stokes lines in nonlinear ordinary differential equations. Proc. R. Soc. Lond. A 454, 2733–2755.CrossRefGoogle Scholar
Chapman, S.J. & Kozyreff, G. 2009 Exponential asymptotics of localised patterns and snaking bifurcation diagrams. Physica D 238 (3), 319–354.CrossRefGoogle Scholar
Chapman, S.J. & Vanden-Broeck, J.-M. 2006 Exponential asymptotics and gravity waves. J. Fluid Mech. 567, 299–326.CrossRefGoogle Scholar
Chen, B. & Saffman, P.G. 1979 Steady gravity-capillary waves on deep water–1. Weakly nonlinear waves. Stud. Appl. Maths 60 (3), 183–210.CrossRefGoogle Scholar
Chen, B. & Saffman, P.G. 1980 a Numerical evidence for the existence of new types of gravity waves of permanent form on deep water. Stud. Appl. Maths 62 (1), 1–21.CrossRefGoogle Scholar
Chen, B. & Saffman, P.G. 1980 b Steady gravity-capillary waves on deep water–II. Numerical results for finite amplitude. Stud. Appl. Maths 62 (2), 95–111.CrossRefGoogle Scholar
Cox, C.S. 1958 Measurements of slopes of high-frequency wind waves. J. Mar. Res. 16, 199–225.Google Scholar
Crapper, G.D. 1957 An exact solution for progressive capillary waves of arbitrary amplitude. J. Fluid Mech. 2 (6), 532–540.CrossRefGoogle Scholar
Crapper, G.D. 1970 Non-linear capillary waves generated by steep gravity waves. J. Fluid Mech. 40 (1), 149–159.CrossRefGoogle Scholar
Dias, F. & Vanden-Broeck, J.-M. 2004 Trapped waves between submerged obstacles. J. Fluid Mech. 509, 93–102.CrossRefGoogle Scholar
Ebuchi, N., Kawamura, H. & Toba, Y. 1987 Fine structure of laboratory wind-wave surfaces studied using an optical method. Boundary-Layer Meteorol. 39 (1–2), 133–151.CrossRefGoogle Scholar
Hocking, G.C., Holmes, R.J. & Forbes, L.K. 2013 A note on waveless subcritical flow past a submerged semi-ellipse. J. Engng Maths 81 (1), 1–8.CrossRefGoogle Scholar
Holmes, R.J., Hocking, G.C., Forbes, L.K. & Baillard, N.Y. 2013 Waveless subcritical flow past symmetric bottom topography. Eur. J. Appl. Maths 24 (2), 213–230.CrossRefGoogle Scholar
Hung, L.-P. & Tsai, W.-T. 2009 The formation of parasitic capillary ripples on gravity–capillary waves and the underlying vortical structures. J. Phys. Oceanogr. 39 (2), 263–289.CrossRefGoogle Scholar
Longuet-Higgins, M.S. 1963 The generation of capillary waves by steep gravity waves. J. Fluid Mech. 16, 138–159.CrossRefGoogle Scholar
Longuet-Higgins, M.S. 1989 Capillary–gravity waves of solitary type on deep water. J. Fluid Mech. 200, 451–470.CrossRefGoogle Scholar
Longuet-Higgins, M.S. 1995 Parasitic capillary waves: a direct calculation. J. Fluid Mech. 301, 79–107.CrossRefGoogle Scholar
Moreira, R.M. & Peregrine, D.H. 2010 Nonlinear interactions between a free-surface flow with surface tension and a submerged cylinder. J. Fluid Mech. 648, 485.CrossRefGoogle Scholar
Mui, R.C.Y. & Dommermuth, D.G. 1995 The vortical structure of parasitic capillary waves. Trans. ASME J. Fluids Engng 117, 355–361.CrossRefGoogle Scholar
Okamoto, H. & Shõji, M. 2001 The Mathematical Theory of Permanent Progressive Water-Waves. World Scientific.CrossRefGoogle Scholar
Perlin, M., Lin, H. & Ting, C.-L. 1993 On parasitic capillary waves generated by steep gravity waves: an experimental investigation with spatial and temporal measurements. J. Fluid Mech. 255, 597–620.CrossRefGoogle Scholar
Schwartz, L.W. & Vanden-Broeck, J.-M. 1979 Numerical solution of the exact equations for capillary–gravity waves. J. Fluid Mech. 95 (1), 119–139.CrossRefGoogle Scholar
Shelton, J. & Trinh, P.H. 2021 Exponential asymptotics for steady-state parasitic gravity-capillary waves. arXiv:2106.09495.Google Scholar
Shimizu, C. & Shōji, M. 2012 Appearance and disappearance of non-symmetric progressive capillary–gravity waves of deep water. Japan J. Ind. Appl. Maths 29 (2), 331–353.CrossRefGoogle Scholar
Stokes, G.G. 1847 On the theory of oscillatory waves. Trans. Camb. Phil. Soc. 8, 441–455.Google Scholar
Toland, J.F. 1996 Stokes waves. Topol. Method. Nonlinear Anal. 7 (1), 1.CrossRefGoogle Scholar
Trinh, P.H. & Chapman, S.J. 2013 New gravity-capillary waves at low speeds. Part 1: linear theory. J. Fluid Mech. 724, 367–391.CrossRefGoogle Scholar
Vanden-Broeck, J.-M. 2010 Gravity-Capillary Free-Surface Flows. Cambridge University Press.CrossRefGoogle Scholar
Wilton, J.R. 1915 On ripples. Phil. Mag. 29 (173), 688–700.CrossRefGoogle Scholar
Zufiria, J.A. 1987 a Non-symmetric gravity waves on water of infinite depth. J. Fluid Mech. 181, 17–39.CrossRefGoogle Scholar
Zufiria, J.A. 1987 b Symmetry breaking in periodic and solitary gravity-capillary waves on water of finite depth. J. Fluid Mech. 184, 183–206.CrossRefGoogle Scholar