Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-17T03:24:25.305Z Has data issue: false hasContentIssue false
  • English
  • Français

On the starting vortex generated by a translating and rotating flat plate

Published online by Cambridge University Press:  10 November 2020

D. I. Pullin  and
John E. Sader Open the ORCID record for John E. Sader [Opens in a new window]
D. I. Pullin*
Affiliation:
Graduate Aerospace Laboratories, California Institute of Technology, Pasadena, CA91125, USA
John E. Sader
Affiliation:
ARC Centre of Excellence in Exciton Science, School of Mathematics and Statistics, University of Melbourne, Victoria3010, Australia Department of Physics, California Institute of Technology, Pasadena, CA91125, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

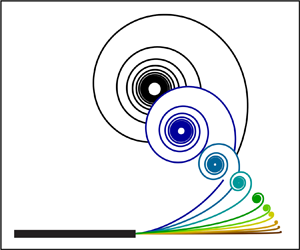
We consider the trailing-edge vortex produced in an inviscid fluid by the start-up motion of a two-dimensional flat plate. A general starting motion is studied that includes the initial angle-of-attack of the plate (which may be zero), individual time power laws for plate translational and rotational speeds and the pivot position for plate rotation. A vortex-sheet representation for a start-up separated flow at the trailing edge is developed whose time-wise evolution is described by a Birkhoff–Rott equation coupled to an appropriate Kutta condition. This description includes convection by the outer flow, rotation and vortex-image self-induction. It admits a power-law similarity solution for the (small-time) primitive vortex, leading to an equation set where each term carries its own time-wise power-law factor. A set of four general plate motions is defined. Dominant-balance analysis of this set leads to discovery of three distinct start-up vortex-structure types that form the basis for all vortex motion. The properties of each type are developed in detail for some special cases. Numerical and analytical solutions are described and transition between solution types is discussed. Singular and degenerate vortex behaviour is discovered which may be due to the absence of fluid viscosity. An interesting case is start-up motion with zero initial angle of attack coupled to power-law plate rotation for which time-series examples are given that can be compared to high Reynolds number viscous flows.

JFM classification

Vortex Flows: Vortex dynamics Vortex Flows: Vortex shedding
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 906 , 10 January 2021 , A9
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Anton, L. 1939 Ausbildung eines wirbels an der kante einer platte. Ing.-Arch. 10 (6), 411–427.CrossRefGoogle Scholar
Anton, L. 1956 Formation of a vortex at the edge of a flat plate. NACA Tech. Memo 1398.Google Scholar
Auerbach, D. 1987 Experiments on the trajectory and circulation of the starting vortex. J. Fluid Mech. 183, 185–198.CrossRefGoogle Scholar
Birkhoff, G. 1962 Helmholtz and Taylor instability. In Proceedings of the Symp. Appl. Math., vol. 13, pp. 55–76.Google Scholar
Blendermann, W. 1967 Der Spiralwirbel am translatorisch bewegten Kreisbogenprofil: Struktur, Bewegung und Reaktion. Institut für Schiffbau der Univ. Hamburg.Google Scholar
Eldredge, J. D. 2007 Numerical simulation of the fluid dynamics of 2D rigid body motion with the vortex particle method. J. Comput. Phys. 221 (2), 626–648.CrossRefGoogle Scholar
Guiraud, J. P. & Zeytounian, R. K. 1977 A double-scale investigation of the asymptotic structure of rolled-up vortex sheets. J. Fluid Mech. 79 (1), 93–112.CrossRefGoogle Scholar
Jones, M. A. 2003 The separated flow of an inviscid fluid around a moving flat plate. J. Fluid Mech. 496, 405–441.CrossRefGoogle Scholar
Kaden, H. 1931 Aufwicklung einer unstabilen unstetigkeitsfläche. Ing.-Arch. 2 (2), 140–168.CrossRefGoogle Scholar
Koumoutsakos, P. & Shiels, D. 1996 Simulations of the viscous flow normal to an impulsively started and uniformly accelerated flat plate. J. Fluid Mech. 328, 177–227.CrossRefGoogle Scholar
Krasny, R. 1991 Vortex sheet computations: roll-up, wakes, separation. Lect. Appl. Maths 28 (1), 385–401.Google Scholar
Luchini, P. & Tognaccini, R. 2002 The start-up vortex issuing from a semi-infinite flat plate. J. Fluid Mech. 455, 175–193.CrossRefGoogle Scholar
Luchini, P. & Tognaccini, R. 2017 Viscous and inviscid simulations of the start-up vortex. J. Fluid Mech. 813, 53–69.CrossRefGoogle Scholar
Michelin, S., Smith, S. & Llewellyn, G. 2009 An unsteady point vortex method for coupled fluid–solid problems. Theor. Comput. Fluid Dyn. 23 (2), 127–153.CrossRefGoogle Scholar
Milne-Thomson, L. M. 1996 Theoretical Hydrodynamics. Courier Corporation.Google Scholar
Moore, D. W. 1975 The rolling up of a semi-infinite vortex sheet. Proc. R. Soc. Lond. A 345 (1642), 417–430.Google Scholar
Nitsche, M. & Xu, L. 2014 Circulation shedding in viscous starting flow past a flat plate. Fluid Dyn. Res. 46 (6), 061420.CrossRefGoogle Scholar
Pierce, D. 1961 Photographic evidence of the formation and growth of vorticity behind plates accelerated from rest in still air. J. Fluid Mech. 11 (3), 460–464.CrossRefGoogle Scholar
Prandtl, L. 1924 Über die entstehung von wirbeln in der idealen flüssigkeit, mit anwendung auf die tragflügeltheorie und andere aufgaben. In Vorträge aus dem Gebiete der Hydro-und Aerodynamik (Innsbruck 1922), pp. 18–33. Springer.CrossRefGoogle Scholar
Pullin, D. I. 1978 The large-scale structure of unsteady self-similar rolled-up vortex sheets. J. Fluid Mech. 88 (3), 401–430.CrossRefGoogle Scholar
Pullin, D. I. & Perry, A. E. 1980 Some flow visualization experiments on the starting vortex. J. Fluid Mech. 97 (2), 239–255.CrossRefGoogle Scholar
Pullin, D. I. & Wang, Z. J. 2004 Unsteady forces on an accelerating plate and application to hovering insect flight. J. Fluid Mech. 509, 1–21.CrossRefGoogle Scholar
Rott, N. 1956 Diffraction of a weak shock with vortex generation. J. Fluid Mech. 1 (1), 111–128.CrossRefGoogle Scholar
Saffman, P. G. 1992 Vortex Dynamics. Cambridge University Press.Google Scholar
Tchieu, A. A. & Leonard, A. 2011 A discrete-vortex model for the arbitrary motion of a thin airfoil with fluidic control. J. Fluids Struct. 27 (5-6), 680–693.CrossRefGoogle Scholar
Wagner, H. 1925 Über die entstehung des dynamicshen auftriebes von tragflügeln. Z. Angew. Math. Mech. 5, 17–35.CrossRefGoogle Scholar
Wedemeyer, E. 1961 Ausbildung eines wirbelpaares an den kanten einer platte. Ing.-Arch. 30 (3), 187–200.CrossRefGoogle Scholar
Xu, L. & Nitsche, M. 2015 Start-up vortex flow past an accelerated flat plate. Phys. Fluids 27 (3), 033602.CrossRefGoogle Scholar
Xu, L., Nitsche, M. & Krasny, R. 2017 Computation of the starting vortex flow past a flat plate. Proc. IUTAM 20, 136–143.CrossRefGoogle Scholar